阶乘逆元线性求逆元组合计数牛妹的数学难题

Posted 2022-02-21 行码棋

⭐️前置知识⭐️

1️⃣逆元简介

$a\times b\equiv 1(modp)$,可以称a是b在模p情况下的逆元.
逆元其实就是可以看作倒数

2️⃣阶乘逆元

方式一:
通过费马小定理求逆元：
当p为素数，并且gcd(a,p)=1时，我们有$a^{p-1}\equiv 1(modp)$。那么就有$a^{p-2}\times a\equiv 1(modp)$，则a的逆元就是$a^{p-2}$
下面ksm函数为快速幂

fact[0] = 1;
for(int i = 1; i < N; i++)

	fact[i] = fact[i - 1] * i % mod;
	inv[i] = ksm(fact[i], mod - 2);

---

方式二：

通过式子$\frac{1}{(n+1)!}\times (n+1)=\frac{1}{n!}$倒推接近线性求阶乘逆元

$\frac{1}{(n+1)!}$其实就可以看作$(n+1)!$的逆元

for(int i = 1; i <= n; i++)
	fact[i] = fact[i - 1] * i % mod;
inv[n] = ksm(fact[n], mod - 2);
for(int i = n - 1; i >= 1; i--)
	inv[i] = inv[i + 1] * (i + 1) % mod;

---

3️⃣线性求逆元

求$[1,N-1]$关于mod的逆元时，可以做到在$O(N)$时间内解决

设模数为p
对于当前的i，设$p=k\times i+r$,则

$\begin{array}{rlr}k\times i+r& \equiv 0& (modp)\\ k\times i\times (i^{-1}\times r^{-1})+r\times (i^{-1}\times r^{-1})& \equiv 0& (modp)\\ k\times r^{-1}+i^{-1}& \equiv 0& (modp)\\ i^{-1}& \equiv -k\times r^{-1}& (modp)\\ i^{-1}& \equiv -\lfloor \frac{p}{i}\rfloor \times r^{-1}& (modp)\end{array}$
注意：
$inv[1]$一定要初始化为1，需要从2开始递推，不能从1开始递推

inv[0] = inv[1] = 1;
for(int i = 2; i < N; i++)
	inv[i] = inv[mod % i] * (mod - mod / i) % mod;

同时可以通过线性求逆元求阶乘逆元：
只需要再将逆元用类似阶乘的形式乘起来即可，求得的inv[i]即为$i!$的逆元

for(int i = 2; i < N; i++)
	inv[i] = inv[i - 1] * inv[i] % mod;

---

4️⃣组合数计算

$C_n^m$计算
⭐️方式一：公式计算
计算都是在逆元或者阶乘基础上计算的
$C_n^m=\frac{n!}{m!\ast (n-m)!}$

ll C(ll n, ll m)

	if(n < m) return 0;
	return fact[n] * inv[m] % mod * inv[n - m] % mod;

⭐️方式二：递推方式
需要建表,所以如果计算范围比较大时需要的空间也大
递推公式 ： $C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$

for(int i = 1; i <= n; i++)
	for(int j = 0; j <= i; j++)
	
		if(i == j || j == 0) c[i][j] = 1;
		else c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
	

---

5️⃣题目

链接：
https://ac.nowcoder.com/acm/contest/23481/J

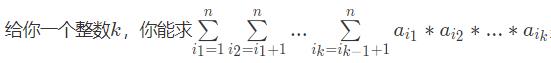
就是在数组中选中k个值相乘，最后把结果相加即可

---

因为数组中的数大小只有三种情况。所以可以根据这个进行切入口。

首先$0$可以不用考虑，接下考虑有$n$个$1$和$m$个$2$，如果上述和式中$1$出现了$i$个，那么$2$需要出现$k-i$个，于是答案为${\sum }_{i=0}^{k}C(n,i$