数据机构与算法之深入解析“柱状图中最大的矩形”的求解思路与算法示例

Posted 2022-02-20 Serendipity·y

一、题目要求

• 给定 n 个非负整数，用来表示柱状图中各个柱子的高度，每个柱子彼此相邻，且宽度为 1 。
• 求在该柱状图中，能够勾勒出来的矩形的最大面积。
• 示例 1：

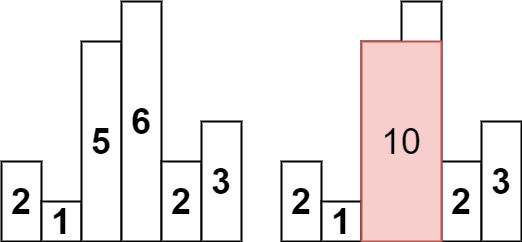
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

• 示例 2：

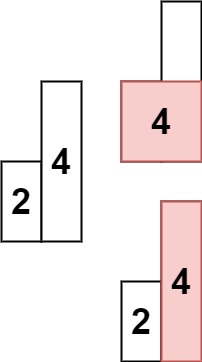
输入： heights = [2,4]
输出： 4

• 提示：
• • 1 <= heights.length <=105；
• • 0 <= heights[i] <= 104。

二、求解算法

① 暴力解法（超时）

• 这道问题的暴力解法比 【数据结构与算法】之深入解析“接雨水”的求解思路与算法示例要好想得多：可以枚举以每个柱形为高度的最大矩形的面积。
• 具体来说是：依次遍历柱形的高度，对于每一个高度分别向两边扩散，求出以当前高度为矩形的最大宽度多少。

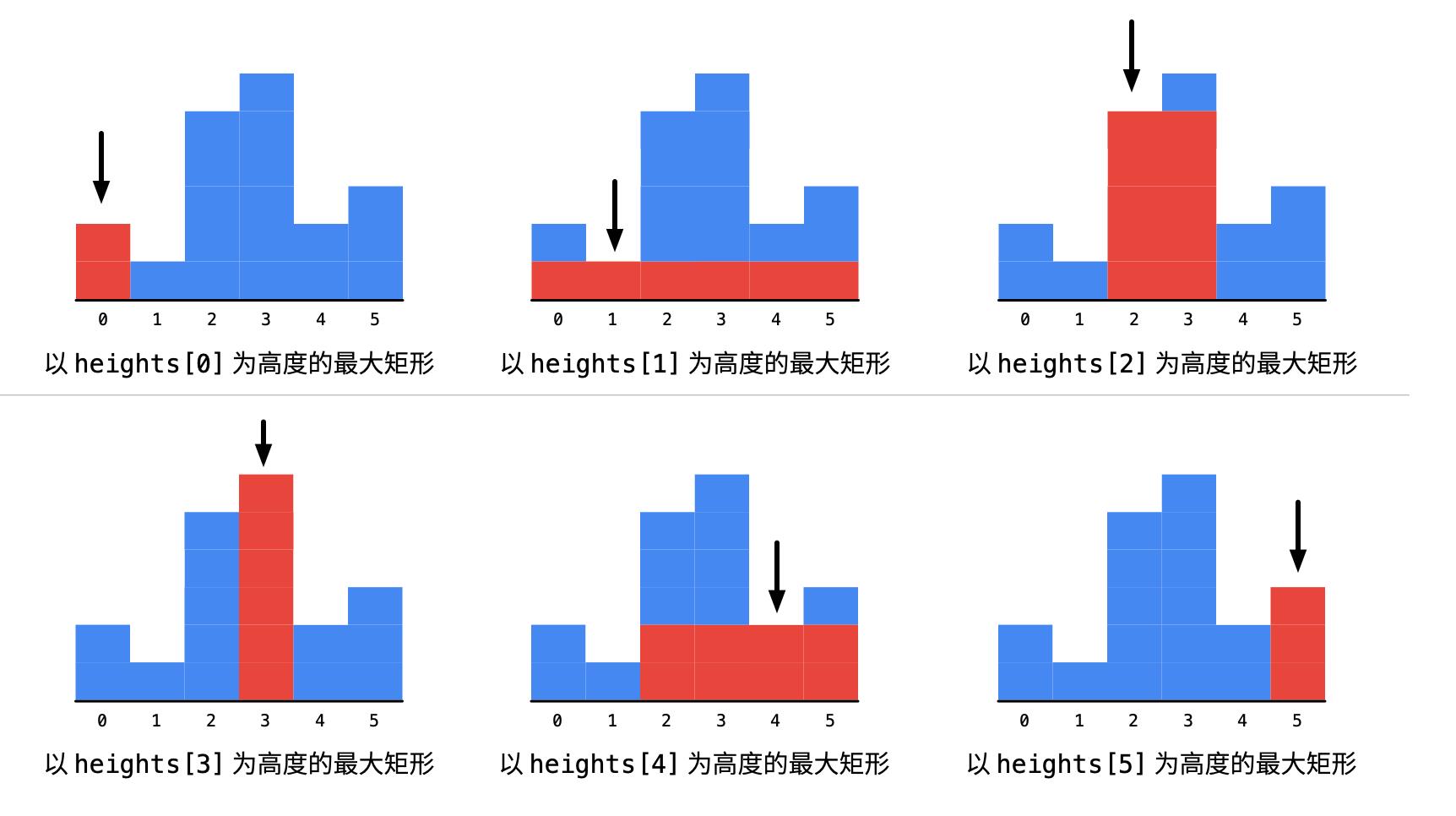
• 为此，需要：
• • 左边看一下，看最多能向左延伸多长，找到大于等于当前柱形高度的最左边元素的下标；
• • 右边看一下，看最多能向右延伸多长；找到大于等于当前柱形高度的最右边元素的下标。
• 对于每一个位置都这样操作，得到一个矩形面积，求出它们的最大值。
• Java 示例：

public class Solution 

    public int largestRectangleArea(int[] heights) 
        int len = heights.length;
        // 特判
        if (len == 0) 
            return 0;
        

        int res = 0;
        for (int i = 0; i < len; i++) 

            // 找左边最后 1 个大于等于 heights[i] 的下标
            int left = i;
            int curHeight = heights[i];
            while (left > 0 && heights[left - 1] >= curHeight) 
                left--;
            

            // 找右边最后 1 个大于等于 heights[i] 的索引
            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) 
                right++;
            

            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        
        return res;
    

• Python 示例：

from typing import List


class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        size = len(heights)
        res = 0

        for i in range(size):
            left = i
            cur_height = heights[i]
            while left > 0 and heights[left - 1] >= cur_height:
                left -= 1

            right = i
            while right < size - 1 and heights[right + 1] >= cur_height:
                right += 1

            max_width = right - left + 1
            res = max(res, max_width * cur_height)
        return res

② 栈

以数组 [2, 1, 5, 6, 2, 3] 为例

• 一开始看到的柱形高度为 2 ，这个时候以这个 2 为高度的最大面积的矩形还不能确定，需要继续向右遍历，如下图：

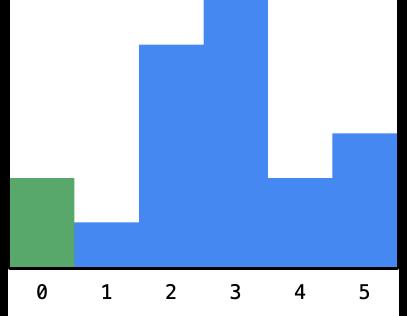
• 然后看到到高度为 1 的柱形，这个时候以这个柱形为高度的矩形的最大面积还是不知道的。但是它之前的以 2 为高度的最大面积的矩形是可以确定的，这是因为这个 1 比 2 小 ，因为这个 1 卡在了这里 2 不能再向右边扩展，如下图：

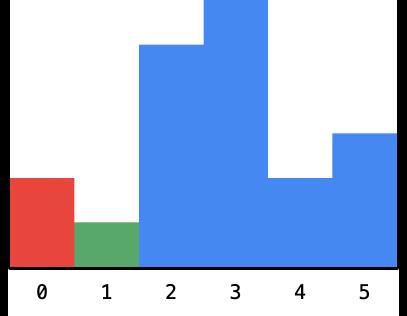
• 计算一下以 2 为高度的最大矩形的面积是 2，其实这个时候，求解这个问题的思路其实已经慢慢打开，如果已经确定了一个柱形的高度，可以无视它，将它以虚框表示，如下图：

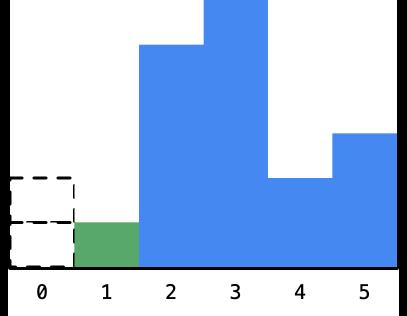
• 遍历到高度为 5 的柱形，同样的以当前看到柱形为高度的矩形的最大面积也是不知道的，因为还要看右边高度的情况，那么它的左右有没有可以确定的柱形呢？没有，这是因为 5 比 1 大，看后面马上就出现了 6，不管是 1 这个柱形还是 5 这个柱形，都还可以向右边扩展：

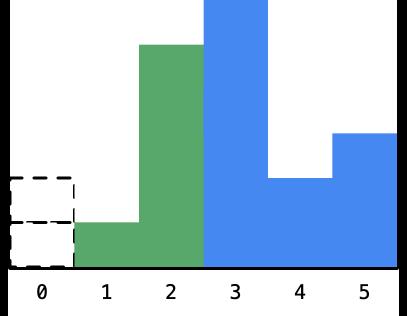
• 再接下来，遍历到高度为 2 的柱形：

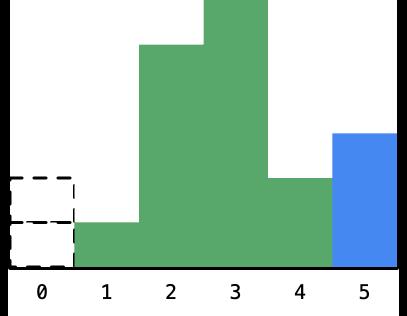
• 发现了一件很神奇的事情，高度为 6 的柱形对应的最大矩形的面积的宽度可以确定下来，它就是夹在高度为 5 的柱形和高度为 2 的柱形之间的距离，它的高度是 6，宽度是 1：

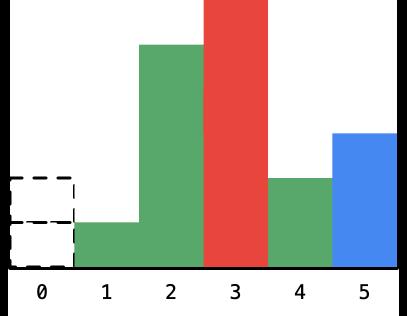
• 将可以确定的柱形设置为虚线：

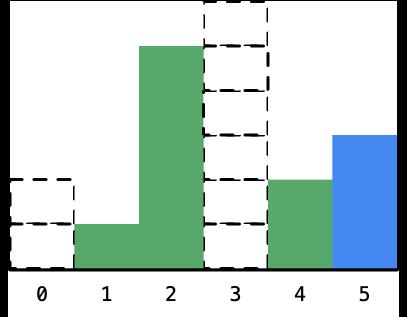
• 接下来柱形 5 对应的最大面积的矩形的宽度也可以确定下来，它是夹在高度为 1 和高度为 2 的两个柱形之间的距离；

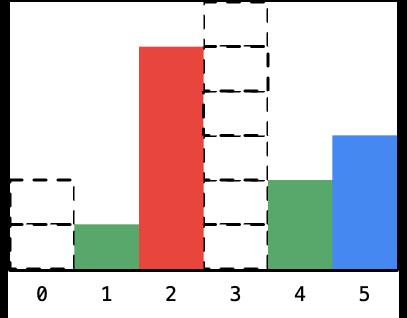
• 确定好以后，将它标成虚线：

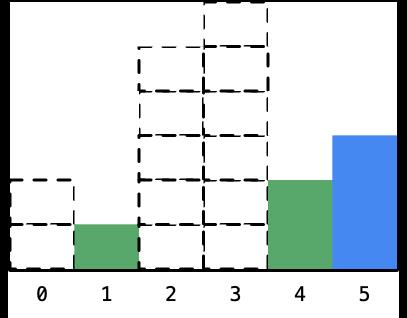
• 可以发现，只要是遇到当前柱形的高度比它上一个柱形的高度严格小的时候，一定可以确定它之前的某些柱形的最大宽度，并且确定的柱形宽度的顺序是从右边向左边。这个现象告诉我们，在遍历的时候需要记录的信息就是遍历到的柱形的下标，它一左一右的两个柱形的下标的差就是这个面积最大的矩形对应的最大宽度。
• 这个时候，还需要考虑的一个细节是，在确定一个柱形的面积的时候，除了右边要比当前严格小，其实还蕴含了一个条件，那就是左边也要比当前高度严格小。
• 那如果是左边的高度和自己相等怎么办呢？之前是只要比当前严格小，我们才可以确定一些柱形的最大宽度，只要是大于或者等于之前看到的那一个柱形的高度的时候，其实都不能确定。因此确定当前柱形对应的宽度的左边界的时候，往回头看的时候，一定要找到第一个严格小于我们要确定的那个柱形的高度的下标。这个时候中间那些相等的柱形其实就可以当做不存在一样，因为它对应的最大矩形和它对应的最大矩形其实是一样的。
• 我们在遍历的时候，需要记录的是下标，如果当前的高度比它之前的高度严格小于的时候，就可以直接确定之前的那个高的柱形的最大矩形的面积，为了确定这个最大矩形的左边界，还要找到第一个严格小于它的高度的矩形，向左回退的时候，其实就可以当中间这些柱形不存在一样。这是因为就是想确定 6 的宽度，6 的宽度确定完了，其实就不需要它了，这个 5 的高度和这个 5 的高度确定完了，也不需要它了。
• 在缓存数据的时候，是从左向右缓存的，我们计算出一个结果的顺序是从右向左的，并且计算完成以后就不再需要了，符合后进先出的特点。因此，需要的这个作为缓存的数据结构就是栈。
• 当确定了一个柱形的高度的时候，我们就将它从栈顶移出，所有的柱形在栈中进栈一次，出栈一次，一开始栈为空，最后也一定要让栈为空，表示这个高度数组里所有的元素都考虑完。
• 最后遍历到最后一个柱形，即高度为 3 的柱形：

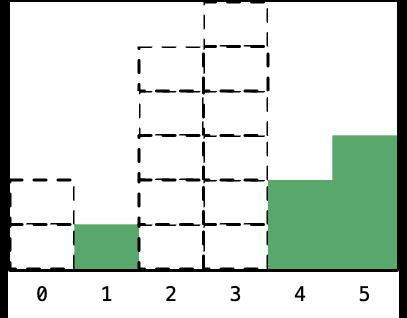
• 接下来我们就要依次考虑还在栈里的柱形的高度，和刚才的方法一样，只不过这个时候右边没有比它高度还小的柱形了，这个时候计算宽度应该假设最右边还有一个下标为 len （这里等于 6） 的高度为 0 （或者 0.5，只要比 1 小）的柱形：

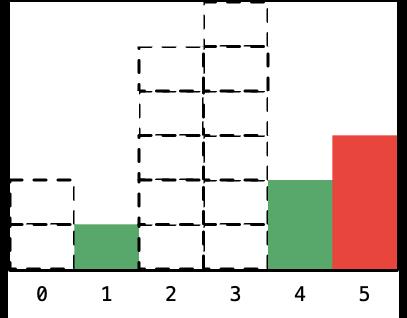
• 下标为 5 ，即高度为 3 的柱形，左边的下标是 4 ，右边的下标是 6 ，因此宽度是 6 - 4 - 1 = 1（两边都不算，只算中间的距离，所以减 1）；算完以后，将它标为虚线：

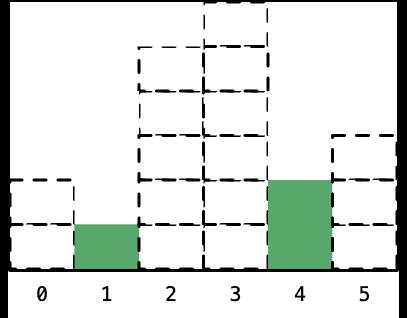
• 下标为 4 ，高度为 2 的柱形，左边的下标是 1 ，右边的下标是 6 ，因此宽度是 6 - 1 - 1 = 4；算完以后，将它标为虚线：

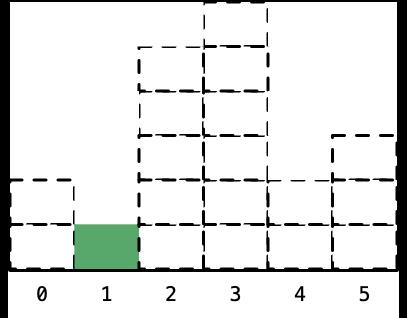
• 最后看下标为 1，高度为 1 的矩形，它的左边和右边其实都没有元素了，它就是整个柱形数组里高度最低的柱形，计算它的宽度，就是整个柱形数组的长度：

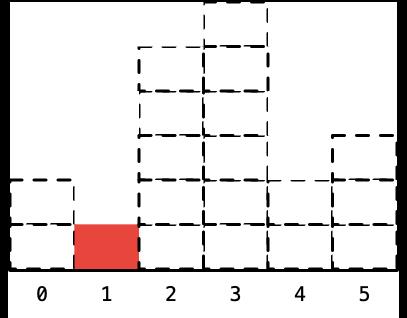
• 到此为止，所有的柱形高度对应的最大矩形的面积就都计算出来了：

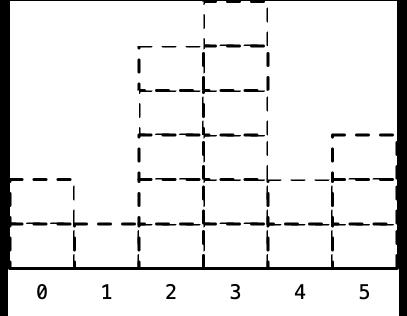
• Java 示例：

import java.util.ArrayDeque;
import java.util.Deque;

public class Solution 

    public int largestRectangleArea(int[] heights) 
        int len = heights.length;
        if (len == 0) 
            return 0;
        
        if (len == 1) 
            return heights[0];
        

        int res = 0;
        Deque<Integer> stack = new ArrayDeque<>(len);
        for (int i = 0; i < len; i++) 
            // 这个 while 很关键，因为有可能不止一个柱形的最大宽度可以被计算出来
            while (!stack.isEmpty() && heights[i] < heights[stack.peekLast()]) 
                int curHeight = heights[stack.pollLast()];
                while (!stack.isEmpty() && heights[stack.peekLast()] == curHeight) 
                    stack.pollLast();
                

                int curWidth;
                if (stack.isEmpty()) 
                    curWidth = i;
                 else 
                    curWidth = i - stack.peekLast() - 1;
                

                // System.out.println("curIndex = " + curIndex + " " + curHeight * curWidth);
                res = Math.max(res, curHeight * curWidth);
            
            stack.addLast(i);
        

        while (!stack.isEmpty()) 
            int curHeight = heights[stack.pollLast()];
            while (!stack.isEmpty() && heights[stack.peekLast()] == curHeight) 
                stack.pollLast();
            
            int curWidth;
            if (stack.isEmpty()) 
                curWidth = len;
             else 
                curWidth = len - stack.peekLast() - 1;
            
            res = Math.max(res, curHeight * curWidth);
        
        return res;
    

• C++ 示例：

#include <iostream>
#include <vector>
#include <stack>

using namespace std;


class Solution 
public:
    int largestRectangleArea(vector<int> &heights) 
        unsigned long size = heights.size();
        if (size == 1) 
            return heights[0];
        
        int res = 0;
        stack<int> stk;
        for (int i = 0; i < size; ++i) 
            while (!stk.empty() && heights[stk.top()] > heights[i]) 
                int length = heights[stk.top()];
                stk.pop();
                int weight = i;
                if (!stk.empty()) 
                    weight = i - stk.top() - 1;
                
                res = max(res, length * weight);
            
            stk.push(i);
        
        while (!stk.empty()) 
            int length = heights[stk.top()];
            stk.pop();
            int weight = size;
            if (!stk.empty()) 
                weight = size - stk.top() - 1;
            
            res = max(res, length * weight);
        
        return res;
    
;