机器学习神经网络识别手写数字(附python源码)
Posted 大拨鼠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习神经网络识别手写数字(附python源码)相关的知识,希望对你有一定的参考价值。
文章目录
非线性假设
我们先来说一下在有线性回归和Logistic回归的基础上,为什么还要用神经网络。
假如有一个如下图所示的监督学习分类问题。
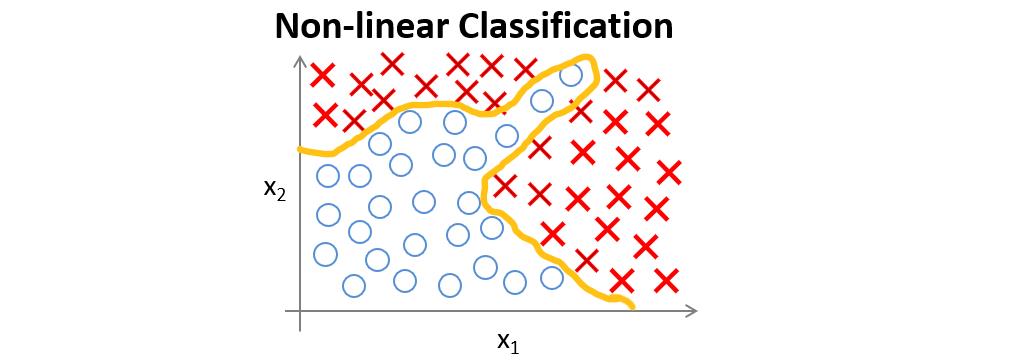
如果运用Logistic回归来解决,则需要构造一个如下图所示包含很多非线性项的Logistic回归函数,当项数足够多时,就能够将样本进行分类。
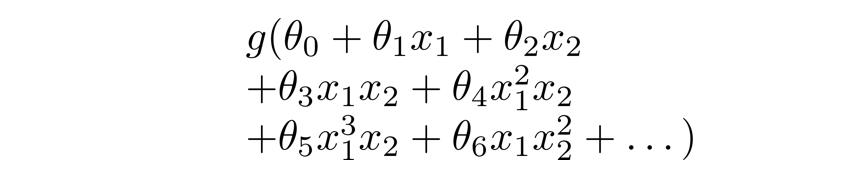
但我们也发现了,这个分类问题仅仅包含两个特征值而已,我们暂且还能将两个特征值的所有交互项包含到多项式中。
但很多时候我们面临的分类问题所包含的特征值远不止两项,如果还用Logistic回归,那么要添加的项是非常多的。
下面我们来看看神经网络是如何解决这一问题的。
神经元与大脑
现在我们用如下模型来将神经元模拟成一个逻辑单元,左边箭头为输入,右边箭头为输出。
有时我们会称该逻辑单元为带有sigmoid或者logistic激活函数的人工神经元。
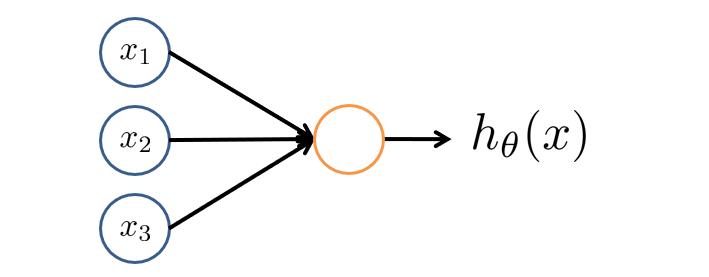
神经网络就是由多个神经元连接在一起的集合,如下图所示。
神经网络的第一层称为输入层,输入特征值。
第二层称为隐藏层,实际上任何非输入层和非输出层都被称为隐藏层,后面我们会提到。
第三层称为输出层,输出假设结果。
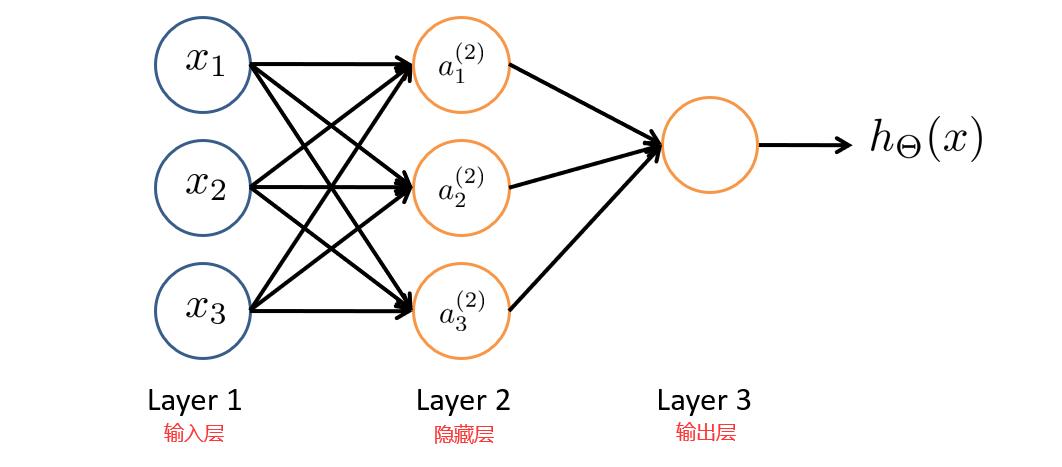
为了解释这个神经网络具体的计算步骤我们再解释一下上图中的一些记号。
a i ( j ) a^(j)_i ai(j):表示第 j j j层的第 i i i个激活项。
θ ( j ) \\theta^(j) θ(j):表示权重矩阵,控制第 j j j层到第 j + 1 j+1 j+1层的映射。
那么,隐藏层三个激活值可表示成如下sigmoid函数值:
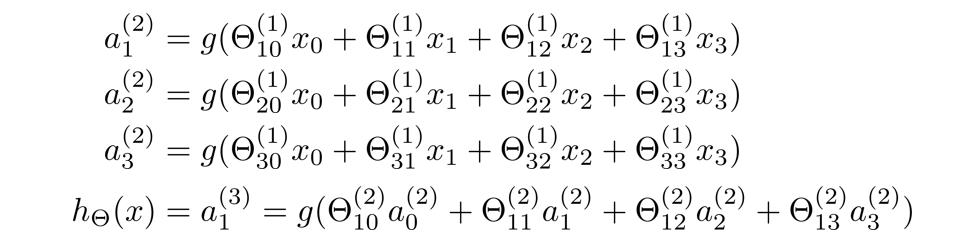
这样我们就更直观地看出了权重矩阵 θ ( 1 ) \\theta^(1) θ(1)控制着第一层到第二层的映射,并且 θ ( 1 ) \\theta^(1) θ(1)是一个 3 × 4 3×4 3×4的矩阵。
权重矩阵 θ ( 2 ) \\theta^(2) θ(2)控制着第二层到第三层的映射,并且 θ ( 2 ) \\theta^(2) θ(2)是一个 1 × 4 1 ×4 1×4的矩阵。
如果一个神经网络的第 j j j层有 s j s_j sj个单元,第 j + 1 j+1 j+1层有 s j + 1 s_j+1 sj+1个单元,则权重矩阵 θ ( j ) \\theta^(j) θ(j)是一个 s j + 1 × ( s j + 1 ) s_j+1×(s_j+1) sj+1×(sj+1)的矩阵。
经过上面的分析,我们得出了以下步骤:先通过前三个方程计算出三个隐藏单元的激活值,然后利用这些激活值计算 h θ ( x ) h_\\theta(x) hθ(x),最后输出。
正向传播:向量化实现
为了实现向量化,接下来我们定义一些额外的项。
我们做如下替换
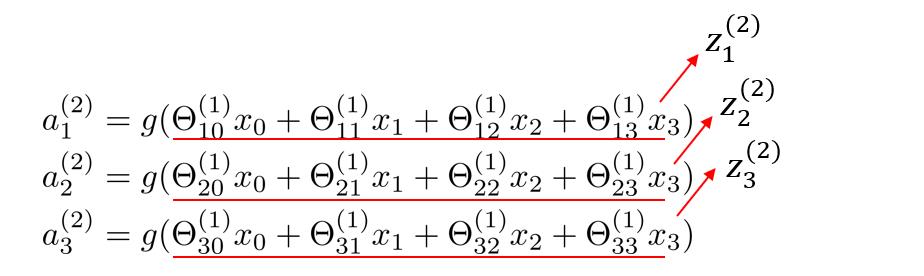
现在我们发现了上面的的数字块似乎对应了矩阵向量乘法,接下来我们就能进行
神经网络的向量化了。
下面我们将 x x x定义为:
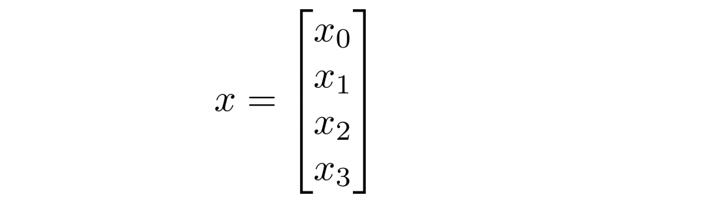
将 z ( 2 ) z^(2) z(2)定义为:
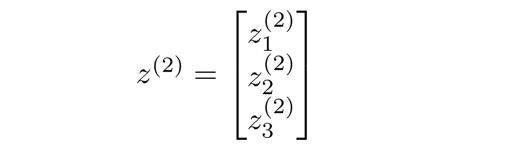
于是有
z ( 2 ) = θ ( 1 ) x z^(2)=\\theta^(1)x z(2)=θ(1)x
求出了 z ( 2 ) z^(2) z(2), a ( 2 ) a^(2) a(2)也就可以求出来了
a ( 2 ) = g ( z ( 2 ) ) a^(2)=g(z^(2)) a(2)=g(z(2))
至此,第一层到第二层的映射解决了,现在来看第二层到第三层的映射:
我们需要在前面求得的 a ( 2 ) a^(2) a(2)中添加一个偏置项 a 0 ( 2 ) = 1 a^(2)_0=1 a0(2)=1
那么 z ( 3 ) = θ ( 2 ) a ( 2 ) z^(3)=\\theta^(2)a^(2) z(3)=θ(2)a(2)
最终 h θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) h_\\theta(x)=a^(3)=g(z^(3)) hθ(x)=a(3)=g(z(3))
好了,来到这里估计大家都晕了,再来回顾一下整个求算过程吧。
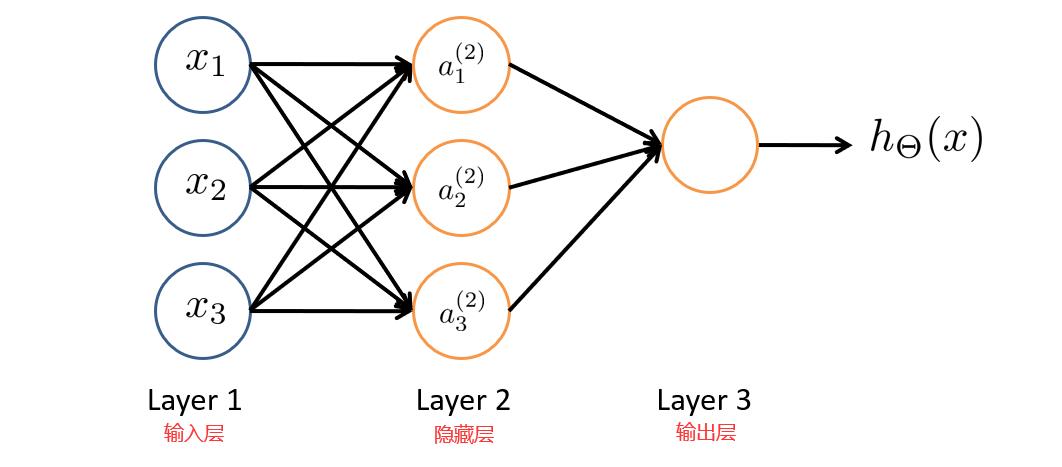
从输入单元的激活项开始,向前传播给隐藏层,计算出隐藏层的激活项,然后继续向前传播,再计算输出层的激活项,这个从输入层到隐藏层再到输出层的过程就叫向前传播。
神经网络中的特征值
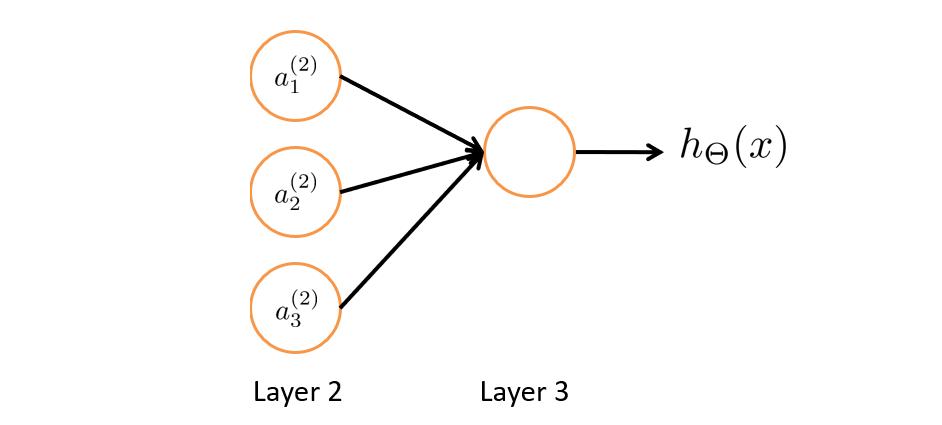
如下图我们先把输入层暂时去掉,其实思路就和Logistic回归一样了,就是通过第二层的特征值,然后利用第三层的逻辑回归单元来预测 h θ ( x ) h_\\theta(x) hθ(x)的值。
神经网络和Logistic回归不同的是,Logistic回归的特征值 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3是数据集直接给出的,但神经网络的特征值并不是原来的特征值 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,还要向前传播计算得到新的 a 1 ( 2 ) 、 a 2 ( 2 ) 、 a 3 ( 2 ) a^(2)_1、a^(2)_2、a^(2)_3 a1(2)、a2(2)、a3(2)作为新的特征值。
代价函数
假设我们有如下训练集:
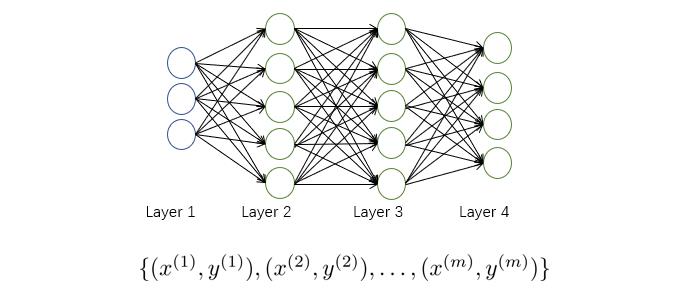
我们用 L L L表示神经网络的层数, s l s_l sl表示第 l l l层中神经元的个数(不包含偏置项)。
这里的输出单元有四个,输出的 h θ ( x ) h_\\theta(x) hθ(x)是一个四维向量,即输出的预测值 y y y为以下几个情况:
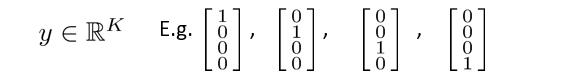
在神经网络中,我们使用的代价函数 是逻辑回归中使用的代价函数的一般形式:
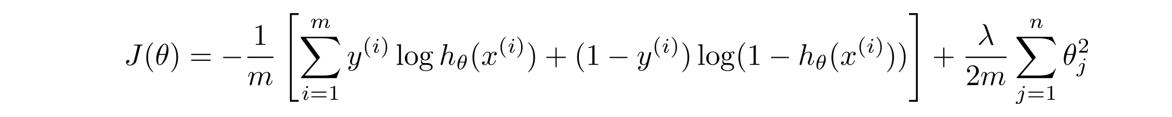
但由于 y y y是一个k(k=4)维向量,因此代价函数改造为:
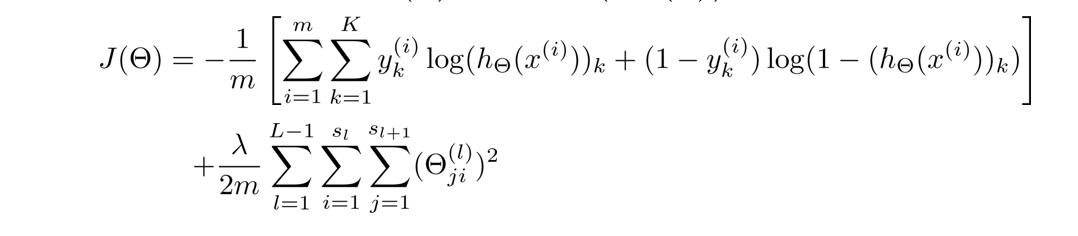
这里稍微解释一下这个代价函数,首先看第一项的求和,这里输出有四个单元,故k=4,其实就是在逻辑函数的输出的基础上,依次把4个代价函数加起来。
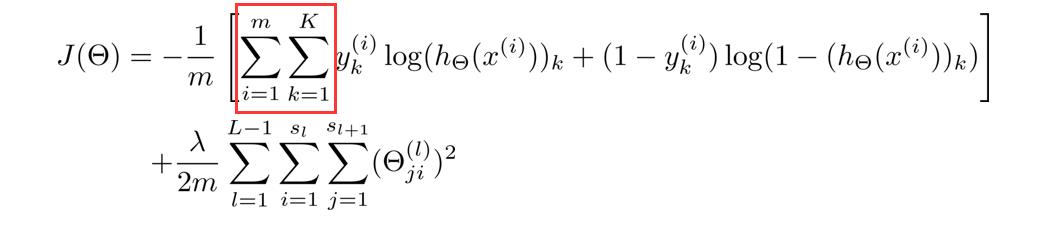
再看看正规项的求和,这里有三个求和号,由于权重矩阵 θ ( j ) \\theta^(j) θ(j)是一个 s j + 1 × ( s j + 1 ) s_j+1×(s_j+1) sj+1×(sj+1)的矩阵,但由于不包含偏差项,少了一列,所以变成 s j + 1 × s j s_j+1×s_j sj+1×sj,故正规项是对每一层的权重矩阵求和,再加起来。

反向传播算法
在得到神经网络的代价函数后,按照惯例下一步我们我们要做的就是最小化函数,而导数项的计算则需要用到反向传播算法。
首先我们来回顾一下正向传播:
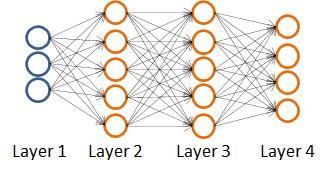
计算步骤如下:
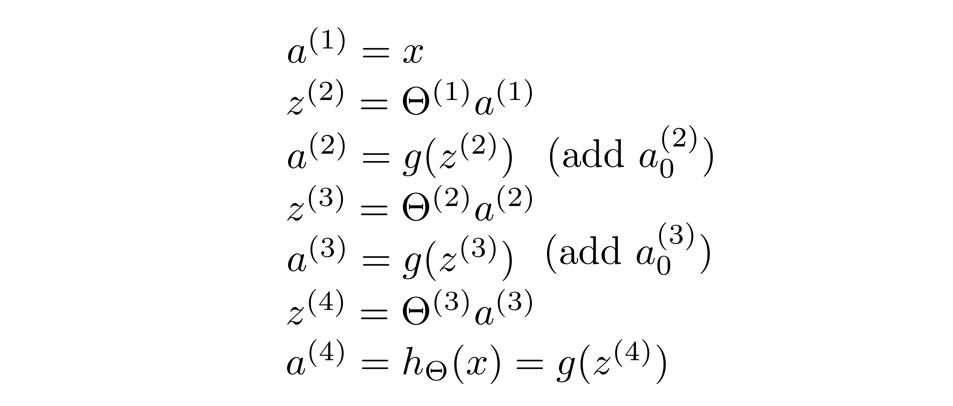
下面来介绍一下这个反向传播:
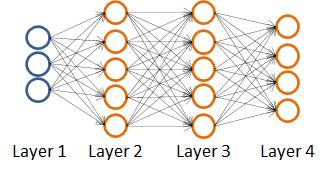
首先我们用 δ j ( l ) \\delta^(l)_j δj(l)表示第 l l l层第 j j j个单元的激活值的误差。
我们以上图四层(L=4)的神经网络为例
如第四层第 j j