LeetCode刷题笔记-动态规划-day4

Posted 2022-02-19 LL.LEBRON

文章目录

• LeetCode刷题笔记-动态规划-day4
• • 55. 跳跃游戏
  • • 1.题目
    • 2.解题思路
    • 3.代码
  • 45. 跳跃游戏 II
  • • 1.题目
    • 2.解题思路
    • 3.代码

LeetCode刷题笔记-动态规划-day4

55. 跳跃游戏

1.题目

原题链接：55. 跳跃游戏

2.解题思路

算法：贪心

我们用变量j表示从前i-1个位置跳能跳到的最远位置，遍历数组：

1. 如果当前位置i大于了j，表示我们从前i-1个位置中跳不到这里，因此也不能跳到最后一个位置，直接返回false
2. 如果可以跳到i，则更新前i个位置可达到的最远距离j的值： j=max(j,i+nums[i]);

最后如果j达到了最后一个数就说明成功了，返回true

3.代码

class Solution 
public:
    bool canJump(vector<int>& nums) 
        for(int i=0,j=0;i<nums.size();i++)
            if(j<i) return false;
            j=max(j,i+nums[i]);
        
        return true;
    
;

45. 跳跃游戏 II

1.题目

原题链接：45. 跳跃游戏 II

2.解题思路

算法：动态规划+贪心

我们用f[i]表示从起点跳到i点所需的最小步数。初始化f[0]=0

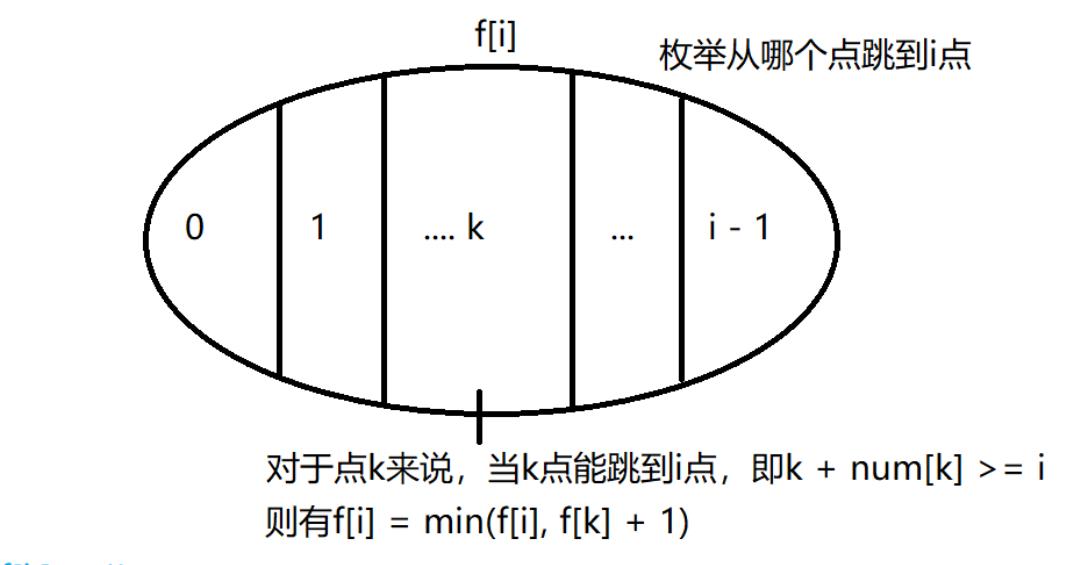
我们发现f[i]是具有单调性的，也就是f[i + 1] >= f[i]。因为我们如果可以跳到f[i+1]是一定可以跳到f[i]的。

如果我们使用两遍循环动态规划的话，在更新每个点的最小值的时候是需要遍历所有能跳到i的点的，而f[i]有了单调性后，我们只需要用第一个能跳到i的点更新就可以，这样最后的步数一定是最小的。

3.代码

class Solution 
public:
    int jump(vector<int>& a) 
        int n=a.size();
        vector<int> f(n);
        for(int i=1,j=0;i<n;i++)
            while(j+a[j]<i) j++;
            f[i]=f[j]+1;
        
        return f[n-1];
    
;