树-面试题

Posted 2022-02-18 nogos

面试题

树的遍历

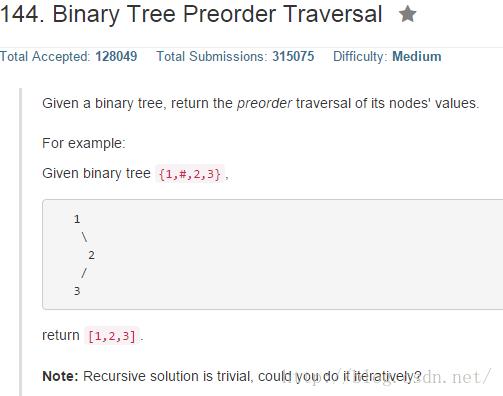
分析

根据前序遍历访问的顺序，优先访问根结点，然后再分别访问左孩子和右孩子。即对于任一结点，其可看做是根结点，因此可以直接访问，访问完之后，若其左孩子不为空，按相同规则访问它的左子树；当访问完其左子树后，再访问它的右子树。因此其处理过程如下：

对于任一结点P：

1)访问结点P，并将结点P入栈;

2)判断结点P的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P;若不为空，则将P的左孩子置为当前的结点P; 

3)直到P为NULL并且栈为空则遍历结束。

public List<Integer> preorderTraversal(TreeNode root) 
	List<Integer> list=new LinkedList<Integer>();
	if(root==null) return list;
	Stack<TreeNode> stack=new Stack<TreeNode>();
	TreeNode p=root;
	while(p!=null||!stack.isEmpty())
		while(p!=null)
			list.add(p.val);
			stack.push(p);
			p=p.left;
		
		p=stack.pop();
		p=p.right;
	 
	return list; 

分析

根据中序遍历的顺序，对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点，然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。因此其处理过程如下：

对于任一结点P，

  1)若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；

  2)若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；

  3)直到P为NULL并且栈为空则遍历结束

public List<Integer> inorderTraversal(TreeNode root) 
	List<Integer> list=new LinkedList<Integer>();
	if(root==null) return list;
	Stack<TreeNode> stack=new Stack<TreeNode>();
	TreeNode p=root;
	while(p!=null||!stack.isEmpty())
		while(p!=null) 
			stack.push(p);
			p=p.left;
		
		p=stack.pop();
		list.add(p.val);
		p=p.right;
	 
	return list; 

分析

 后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中，要保证左孩子和右孩子都已被访问后才能访问根结点，这就为流程的控制带来了难题。

      第一种思路：对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问，因此其右孩子还未被访问。所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问，这样才能保证了正确的访问顺序。可以看出，在这个过程中，右子数不为空的结点都会两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要利用哈希表来标识该结点是否是第一次出现在栈顶。

public List<Integer> postorderTraversal(TreeNode root) 
	List<Integer> list=new LinkedList<Integer>();
	Map<TreeNode,Boolean> visit=new HashMap<TreeNode,Boolean>();
	if(root==null) return list;
	Stack<TreeNode> stack=new Stack<TreeNode>();
	TreeNode p=root;
	while(p!=null||!stack.isEmpty())
		while(p!=null) 
			stack.push(p);
			p=p.left;
		
		p=stack.peek();
		if(p.right!=null)
			if(visit.get(p)==null)
				visit.put(p, true);
				//第一次处理右子树
				p=p.right;
			
			else
				list.add(p.val);
				stack.pop();
				p=null;
			
		else 
			list.add(p.val);
			stack.pop();
			p=null;
		
		
	 
	return list; 

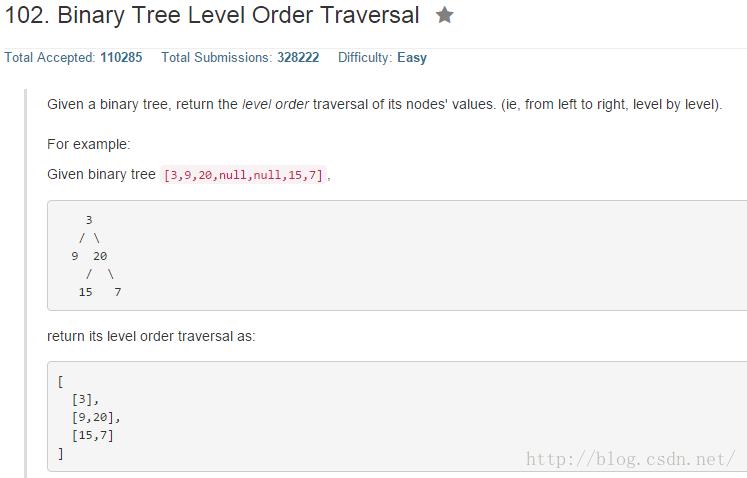
分析

数的层次遍历，即广度优先遍历，利用队列实现。

public List<List<Integer>> levelOrder(TreeNode root) 
	List<List<Integer>> levels=new ArrayList<List<Integer>>(); 
	if(root==null)return levels;
	Queue<TreeNode> queue=new LinkedList<TreeNode>();
	queue.add(root); 
	while(!queue.isEmpty())
		List<Integer> list=new ArrayList<Integer>();
		Queue<TreeNode> nextQueue=new LinkedList<TreeNode>();
		while(!queue.isEmpty())
			TreeNode node=queue.poll();
			list.add(node.val);
			if(node.left!=null)nextQueue.add(node.left);
			if(node.right!=null)nextQueue.add(node.right);
		 
		queue=nextQueue;
		levels.add(list);
	
	return levels;

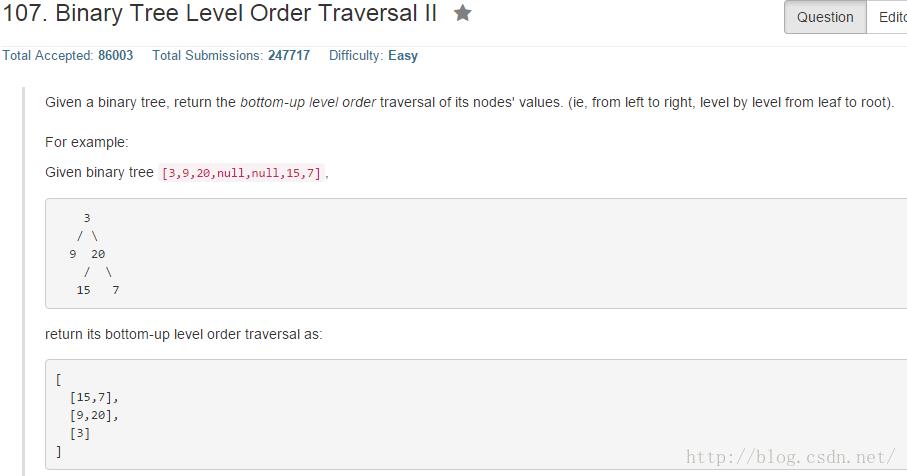
分析

只需将上题结果逆序即可。

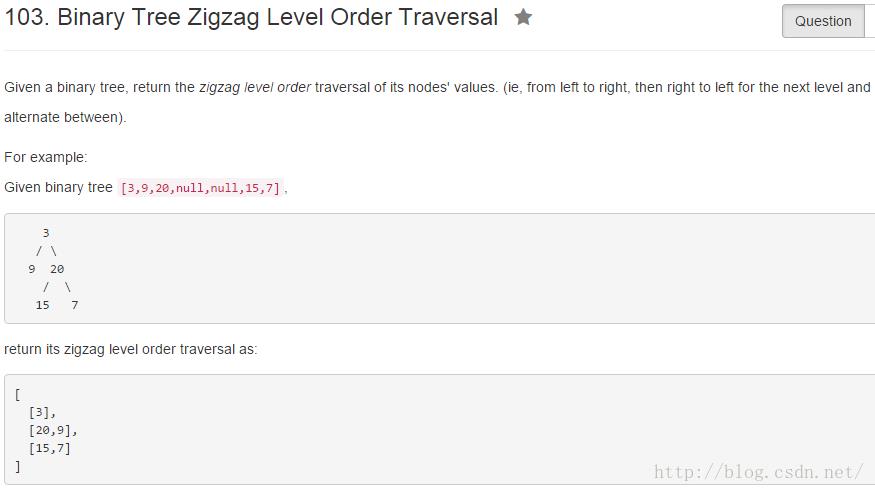
分析

public List<List<Integer>> zigzagLevelOrder(TreeNode root) 
	List<List<Integer>> levels=new LinkedList<List<Integer>>();
	if(root==null) return levels;
	Queue<TreeNode> queue=new LinkedList<TreeNode>();
	queue.add(root);
	int mark=0;
	while(!queue.isEmpty())
		List<Integer> list=new ArrayList<Integer>();
		Queue<TreeNode> nextqueue=new LinkedList<TreeNode>();
		while(!queue.isEmpty())
			TreeNode node=queue.poll();
			list.add(node.val);
			if(node.left!=null)nextqueue.add(node.left);
			if(node.right!=null)nextqueue.add(node.right);
		 
		queue=nextqueue;
		if(mark==1)
			Collections.reverse(list);
		mark=(mark+1)%2;
		levels.add(list);
	
	return levels;

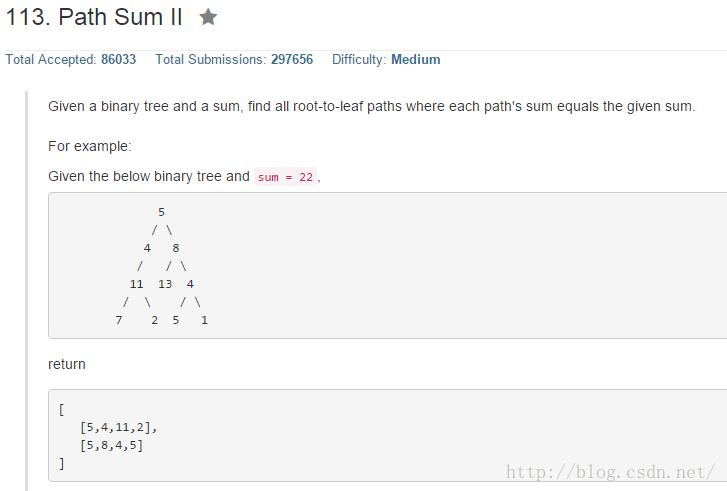
分析

采用后序遍历，栈中的元素即为路径。

public List<List<Integer>> pathSum(TreeNode root, int sum) 
	List<List<Integer>> res=new ArrayList<List<Integer>>();
	if(root==null) return res;
	Map<TreeNode,Boolean> visit=new HashMap<TreeNode,Boolean>();
	Stack<TreeNode> stack=new Stack<TreeNode>();
	int nowSum=0;
	TreeNode p=root;
	while(p!=null||!stack.isEmpty())
		while(p!=null) 
			stack.push(p);
			nowSum+=p.val;
			p=p.left;
		
		p=stack.peek();
		if(p.left==null&&p.right==null&&sum==nowSum)
			List<Integer> r=new ArrayList<Integer>();
			for(Object i:stack.toArray())
				r.add((Integer)((ListNode)i).val);
			res.add(r);
		
		if(p.right!=null)
			if(visit.get(p)==null)
				visit.put(p, true);
				//第一次处理右子树
				p=p.right;
			
			else
				nowSum-=p.val;
				stack.pop(); 
				p=null;
			
		else 
			nowSum-=p.val;
			stack.pop();
			p=null;
		
	 
	return res;

树的构建

public TreeNode buildTree(int[] preorder, int[] inorder) 
	int n=preorder.length;
	if(n==0)return null;
	return doBuildTree(preorder,0,n-1,inorder,0,n-1);
    

public TreeNode doBuildTree(int[] preorder,int s1,int e1, int[] inorder,int s2,int e2)
	if(e1<s1)return null;
	int rootindex = 0;
	for(int i=s2;i<=e2;i++)
		if(inorder[i]==preorder[s1])
			rootindex=i;
			break;
		
	
	int leftCount=rootindex-s2;
	TreeNode root=new TreeNode(preorder[s1]);
	root.left=doBuildTree(preorder,s1+1,s1+leftCount,inorder,s2,rootindex-1);
	root.right=doBuildTree(preorder,s1+leftCount+1,e1,inorder,rootindex+1,e2);
	return root;

public TreeNode buildTree(int[] inorder, int[] postorder) 
	int n=inorder.length;
	if(n==0)return null;
	return doBuildTree(inorder,0,n-1,postorder,0,n-1);

public TreeNode doBuildTree(int[] inorder,int s1,int e1, int[] postorder,int s2,int e2)
	if(e1<s1)return null;
	int rootindex = 0;
	for(int i=s1;i<=e1;i++)
		if(inorder[i]==postorder[e2])
			rootindex=i;
			break;
		
	
	int leftCount=rootindex-s1;
	TreeNode root=new TreeNode(postorder[e2]);
	root.left=doBuildTree(inorder,s1,rootindex-1,postorder,s2,s2+leftCount-1);
	root.right=doBuildTree(inorder,rootindex+1,e1,postorder,s2+leftCount,e2-1);
  	return root;

二分查找树

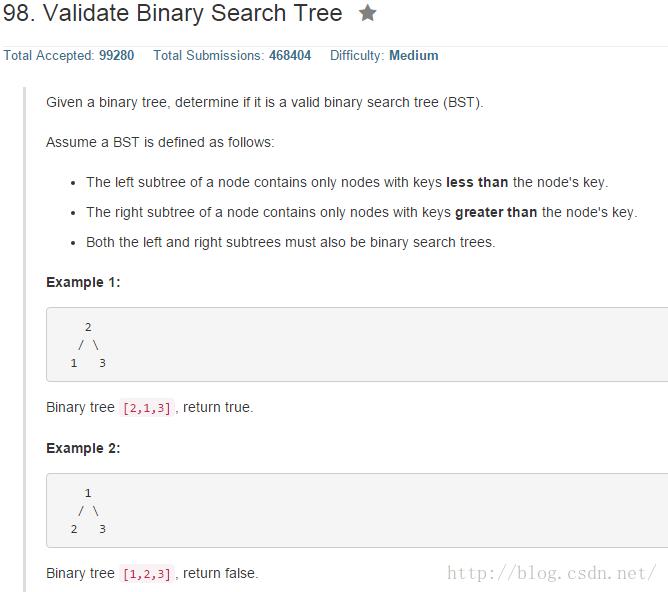
public boolean isValidBST(TreeNode root) 
	//二叉查找树的中序遍历为递增的
	if(root==null)return true;
	List<Integer> list=new LinkedList<Integer>();
	Stack<TreeNode> stack=new Stack<TreeNode>();
	TreeNode p=root;
	while(p!=null||!stack.isEmpty())
		while(p!=null) 
			stack.push(p);
			p=p.left;
		
		p=stack.pop();
		list.add(p.val);
		if(list.size()>=2&&list.get(list.size()-1)<=list.get(list.size()-2))
			return false;
		if(p.right!=null)//处理右子树
			p=p.right;
		else//处理上一层
			p=null;
		 
	 
	return true;

public TreeNode sortedArrayToBST(int[] nums) 
	int n=nums.length;
	if(n==0)return null;
	return doSortedArrayToBST(nums,0,n-1);

public TreeNode doSortedArrayToBST(int[] nums,int start,int end) 
	if(end<start)return null;
	int mid=(start+end)/2;
	TreeNode root=new TreeNode(nums[mid]);
	root.left=doSortedArrayToBST(nums,start,mid-1);
	root.right=doSortedArrayToBST(nums,mid+1,end);
	return root;

public TreeNode sortedListToBST(ListNode head) 
	if(head==null)return null;
	int length=listLength(head); 
	return doSortedListToBST(head,length);

public TreeNode doSortedListToBST(ListNode head,int length) 
	if(length<=0) return null;
	ListNode midListNode=midListNode(head,length);
	int leftlength=listLength(head,midListNode);
	TreeNode root=new TreeNode(midListNode.val);
	root.left=doSortedListToBST(head,leftlength);
	root.right=doSortedListToBST(midListNode.next,length-1-leftlength);
	return root; 

public ListNode midListNode(ListNode head,int length)
	int mid=length/2;
	int mark=length%2==0?1:0;
	ListNode p=head;
	while(mid-->mark)
		p=p.next;
	
	return p; 

public int listLength(ListNode head,ListNode mid)
	int length=0;
	ListNode p=head;
	while(p!=mid)
		length++;
		p=p.next;
	
	return length;

public int listLength(ListNode head)
	int length=0;
	ListNode p=head;
	while(p!=null)
		length++;
		p=p.next;
	
	return length;

二叉树递归

public int minDepth(TreeNode root) 
    if(root==null)return 0;
    return doMinDepth(root);

public int doMinDepth(TreeNode root) 
	if(root==null) return Integer.MAX_VALUE;
	if(root.left==null&&root.right==null) return 1;
	int leftDepth=doMinDepth(root.left);
	int rightDepth=doMinDepth(root.right);
	return 1+Math.min(leftDepth, rightDepth);

public int maxDepth(TreeNode root) 
	if(root==null)return 0;
    return doMaxDepth(root);

public int doMaxDepth(TreeNode root) 
	if(root==null) return Integer.MIN_VALUE;
	if(root.left==null&&root.right==null) return 1;
	int leftDepth=doMaxDepth(root.left);
	int rightDepth=doMaxDepth(root.right);
	return 1+Math.max(leftDepth, rightDepth);

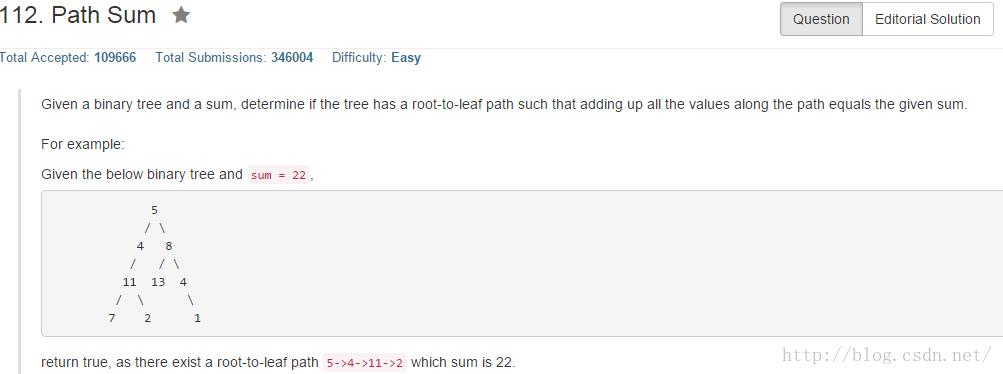
public boolean hasPathSum(TreeNode root, int sum) 
	if(root==null) return false;
	if(root.left==null&&root.right==null&&sum==root.val)
		return true;
	
	return hasPathSum(root.left,sum-root.val)||hasPathSum(root.right,sum-root.val); 

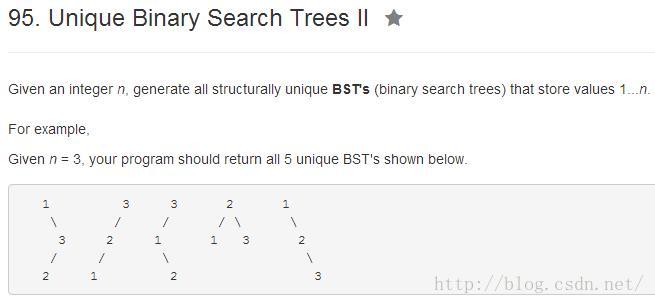
    public List<TreeNode> generateTrees(int n)  
    	if(n==0)
    		return new ArrayList<TreeNode>();
    	
        return buildTree(1,n); 
    
    public List<TreeNode> buildTree(int start,int end)
    	List<TreeNode> res=new ArrayList<TreeNode>();
    	if(start>end)
    		res.add(null);
    		return res;
    	 
    	for(int top=start;top<=end;top++)
    		List<TreeNode> leftTrees=buildTree(start,top-1);
    		List<TreeNode> rightTrees=buildTree(top+1,end);
    		for(TreeNode leftTree:leftTrees)
    			for(TreeNode rightTree:rightTrees)
    				TreeNode topNode=new TreeNode(top);
    				topNode.left=leftTree;
    				topNode.right=rightTree;
    				res.add(topNode);
    			
    		
    	
    	return res;