常用的十大算法-弗洛伊德算法

Posted 2022-02-13 一只懒惰的小虫子

介绍

和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点最短路径的算法，即计算各个顶点之间的最短路径，而迪杰斯特拉算法用于计算某一顶点到其他顶点的最短路径。弗洛伊德算法每一个顶点都是出发访问点，所以需要将每一个顶点都看作被访问的顶点，求出每一个顶点到其他顶点的最短路径。

算法分析

1、设置顶点vi到vk的最短路径已知为Lik,顶点vk到vj的最短路径为Lkj,顶点vi到vj的路径为Lij，则vi到vj的最短路径为：min(Lik+Lkj)，vk的取值为所有顶点，则可获得vi到vj的最短路径。
2、至于vi到vk的最短路径Lik或者vk到vj的最短路径Lkj，是以同样的方式获得。

算法应用

有七个村庄（A,B,C,D,E,F,G），各个村庄的距离用边线表示（权）,如何计算出各村庄到其他各村庄的最短路径。

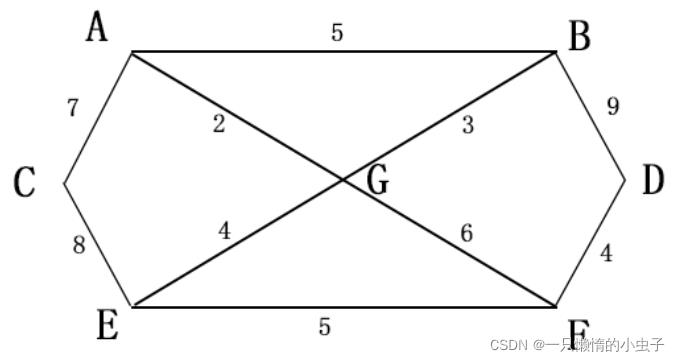
package algorithm;

import java.util.Arrays;

/**
 * @author taoke
 * @desc 弗洛伊德算法
 * @email [e-mail]
 * @date 2022/1/27
 */
public class Floyd 

    private static final int N = 65535;

    public static void main(String[] args) 
        char[] vertex = 'A', 'B', 'C', 'D', 'E', 'F', 'G';
        int[][] matrix = 
                N, 5, 7, N, N, N, 2,
                5, N, N, 9, N, N, 3,
                7, N, N, N, 8, N, N,
                N, 9, N, N, N, 4, N,
                N, N, 8, N, N, 5, 4,
                N, N, N, 4, 5, N, 6,
                2, 3, N, N, 4, 6, N
        ;

        Graph graph = new Graph(vertex, matrix, vertex.length);
        graph.floyd();
        graph.show();
    


    public static class Graph 
        /**
         * 顶点
         */
        private final char[] vertex;
        /**
         * 从各个顶点出发到其他顶点的距离，也是最终的结果
         */
        private final int[][] matrix;
        /**
         * 保存到目标顶点的前驱节点
         */
        private final int[][] pre;

        /**
         * 初始化
         *
         * @param length 顶点长度大小
         * @param matrix 邻接矩阵
         * @param vertex 顶点数组
         */
        public Graph(char[] vertex, int[][] matrix, int length) 
            this.vertex = vertex;
            this.matrix = matrix;
            this.pre = new int[length][length];
            //对pre数组初始化，存放的是前驱顶点的下标
            for (int i = 0; i < length; i++) 
                Arrays.fill(pre[i], i);
            
        

        public void show() 
            for (int i = 0; i < matrix.length; i++) 
                System.out.println();
                for (int j = 0; j < matrix.length; j++) 
                    System.out.print(vertex[i] + "->" + vertex[j] + "=" + matrix[i][j] + "\\t");
                
                System.out.println();
            
        

        /**
         * 弗洛伊德算法
         */
        public void floyd() 
            int len;//变量保存距离
            for (int i = 0; i < matrix.length; i++) 
                for (int j = 0; j < matrix.length; j++) 
                    for (int k = 0; k < matrix.length; k++) 
                        len = matrix[i][j] + matrix[i][k];
                        if (len < matrix[j][k]) 
                            matrix[j][k] = len;//更新距离
                            pre[j][k] = pre[i][k];//更新前驱节点
                        
                    
                
            
        
    

结果