九小时九个人九扇门（01背包）

Posted 2022-02-12 MangataTS

题目链接

https://ac.nowcoder.com/acm/contest/23106/A

题面

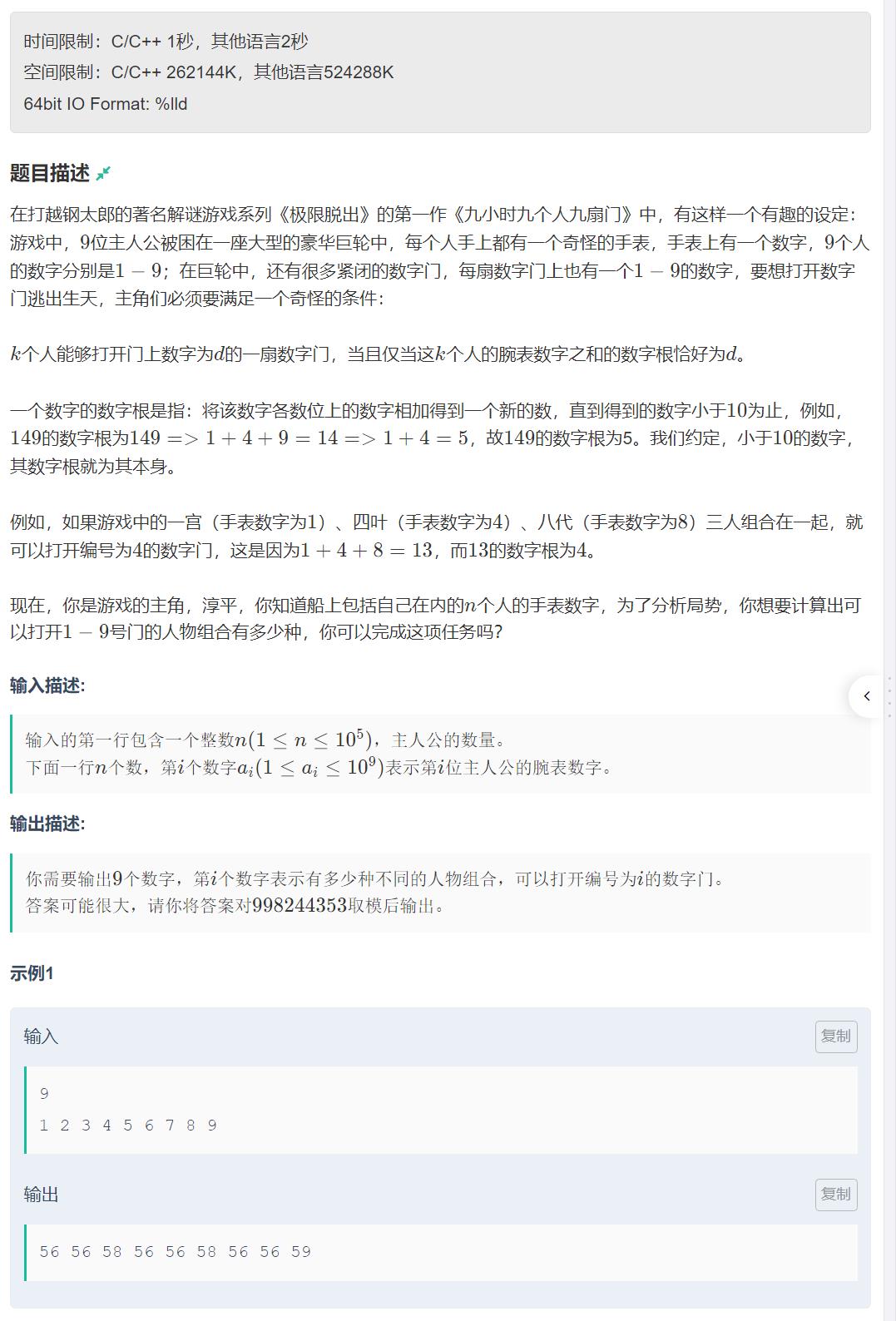
思路

小技巧

一个数的数字根就是它对9取模，当然取模得0的数字跟就是9

做法

我们要求的是从n个人中选一些人,假设这些人的数字用a数组存储，然后将其数字相加，然后求一个数字根，然后将这个数字根的方案数加一，那么这个问题可以转化为01背包问题，因为每一个人的数字只能使用最多一次，也就是每个人的数字存在两种状态：选择or不选择

，那么我们定义一个数组f[i][j]表示的是前i个人选中的数字根方案为j的方案数，我们首先定义一下数字根的表示get(i)表示求i的数字根

那么我们显然能得到状态转移方程
$$\begin{gathered} f[i][j]=f[i][j]+f[i-1][j] \\ f[i][get(j+a[i])]=f[i][get(j+a[i])]+f[i-1][j]; \end{gathered}$$
我们再来看这个状态转移方程，其实就是对应着01背包问题的不选择和选择，因为我们是要将所有状态计数，那么两个方向都要统计，注意的是我们初始化f[0][0]为1，最后再从1到9输出f[n][i]就好了，详情请看代码

代码

#include<bits/stdc++.h>
using namespace std;
//----------------自定义部分----------------
#define ll long long
#define mod 998244353
#define endl "\\n"
#define PII pair<int,int>

int dx[4]=0,-1,0,1,dy[4]=-1,0,1,0;

ll ksm(ll a,ll b) 
	ll ans = 1;
	for(;b;b>>=1LL) 
		if(b & 1) ans = ans * a % mod;
		a = a * a % mod;
	
	return ans;


ll lowbit(ll x)return -x & x;

const int N = 2e6+10;
//----------------自定义部分----------------
ll n,m,q,a[N];
ll f[N][10];//f[i][j]表示的是前i个数选取数字原根为j方案数（取模下）
//每次要么选，要么不选

int get(int x)
	if(x<10)return x;
	int k=0;
	while(x)k+=x%10;x/=10;
	return get(k);


int main()

	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cout.tie(nullptr);
	cin>>n;
	for(int i = 1;i <= n ;++i) 
		cin>>a[i];
	
	f[0][0] = 1;//初始化
	for(int i = 1;i <= n; ++i)
		for(int j = 0;j <= 9; ++j) 
			f[i][j] = (f[i][j] + f[i-1][j]) % mod;//不做选择
			f[i][get(j+a[i])] = (f[i][get(j+a[i])] + f[i-1][j]) % mod;//做选择
		
	
	for(int i = 1;i <= 9; ++i) 
		cout<<f[n][i]<<" \\n"[i==9];
	
	return 0;