2022蓝桥杯学习——5.树状数组和线段树差分
Posted 头发没了还会再长
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022蓝桥杯学习——5.树状数组和线段树差分相关的知识,希望对你有一定的参考价值。
一、树状数组
关于树状数组
原数组是A,树状数组是C,数组A的下标x从1开始,在C中C[x]所在的层数由x的二进制表示有几个0决定,而lowbit(x)返回的是2^k,其中k是x二进制表示中0的个数,C[x]表示的一段区间的和,这个区间是(x-lowbit(x),x],注意是下标表示的区间
int lowbit(x) return x&-x;
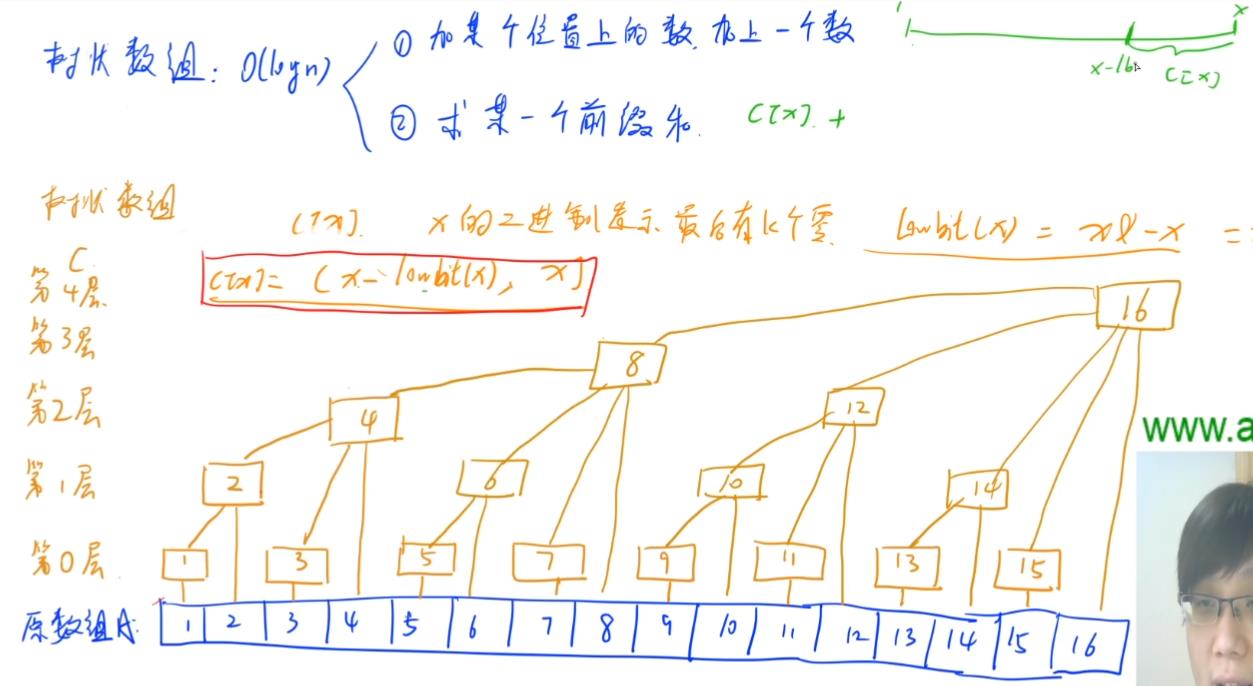
求下标[1~x]的前缀和
//下标x表示的区间是(x-lowbit(x),x],我们求[1,x],所以要递归求[1~x-lowbit(x)],每次都是向前求一段,直到x-lowbit(x)=1 时间复杂度logN
int query(int x)
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=C[i];
return res;
如果给A[x]加上v,更新C[x]
//给A[x]加上v,C[]中所有包括A[x]的点都会加上V,C[x]一定加上V,C[x]的父节点一定加上v,依次往上的一直到根结点都加上v,x的父结点下标是 x+lowbit(x) 时间复杂度logN
A[x]+=v;
for(i=x;i<=n;i+=lowbit(i)) C[i]+=v;
建立一个线段树
//假设A数组全是0,然后每一个位置i加上一个A[i],更新其他位置
for(int i=1;i<=n;i++)
add(i,A[i]);
void add(int x,int v)
for(int i=x;i<=n;i+=lowbit(i)) C[i]+=v;
例题
1.动态求连续区间和
题目描述
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。
数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。
数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35
解题思路
这就是树状数组的模板题,直接用模板求解即可
代码实现+详细注释 C++
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=100010;
int a[N],tr[N];
int n,m;
int lowbit(int x)
return x&-x;
void add(int x,int v)
for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=v;
int query(int x)
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=tr[i];
return res;
int main()
int k,x,y;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) add(i,a[i]);//刚开始将树状数组看成一个全是0 的数组,然后将a一个个加上去
while(m--)
cin>>k>>x>>y;
if(k==0) cout<<query(y)-query(x-1)<<endl;
else add(x,y);
return 0;
2.数星星
题目描述
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。
如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。

例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。
例图中有 1 个 0 级,2 个 1 级,1 个 2 级,1 个 3 级的星星。
给定星星的位置,输出各级星星的数目。
换句话说,给定 N 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
输入格式
第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y 表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
输出格式
N 行,每行一个整数,分别是 0 级,1 级,2 级,……,N−1 级的星星的数目。
数据范围
1≤N≤15000,
0≤x,y≤32000
输入样例:
5
1 1
5 1
7 1
3 3
5 5
输出样例:
1
2
1
1
0
解题思路
因为按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出,对于给出的(xi,yi),它后面给出的星星要么纵坐标比它大,要么横坐标比它大,所以只考虑它前面给出的星星就行,而在它前面给出的星星纵坐标y一定小于等于它,所以只需要考虑前面的星星哪些横坐标也是小于等于它的就行,那就转化成了求横坐标[1~xi]之间有多少星星 原数组A[] 表示每个横坐标下有多少星星,如果求横坐标小于等于x的星星就是求前缀和A[1]+…+A[x],每多一个星星就是这个位置上加上一个 1
代码实现+详细注释 C++
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=32010;
int level[N],tr[N];
int lowbit(int x)
return x&-x;
void add(int x)
for(int i=x;i<N;i+=lowbit(i)) tr[i]++;
int sum(int x)
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=tr[i];
return res;
int main()
int n,m;
cin>>n;
m=n;
while(n--)
int x,y;
cin>>x>>y;
x++;//因为x的取值范围从0开始,但是树状数组从 1 开始,所以每次将横坐标+1
level[sum(x)]++;//在add之前就计算[1~x]之间之间有多少星星,不然add之后会把x也加进去,因为保证同一个位置之前只有一个星星
add(x);
for(int i=0;i<m;i++) cout<<level[i]<<endl;
蓝桥杯真题
1.小朋友排队
题目描述
n 个小朋友站成一排。
现在要把他们按身高从低到高的顺序排列,但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。
开始的时候,所有小朋友的不高兴程度都是 0。
如果某个小朋友第一次被要求交换,则他的不高兴程度增加 1,如果第二次要求他交换,则他的不高兴程度增加 2(即不高兴程度为 3),依次类推。当要求某个小朋友第 k 次交换时,他的不高兴程度增加 k。
请问,要让所有小朋友按从低到高排队,他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样,则他们谁站在谁前面是没有关系的。
输入格式
输入的第一行包含一个整数 n,表示小朋友的个数。
第二行包含 n 个整数 H1,H2,…,Hn,分别表示每个小朋友的身高。
输出格式
输出一行,包含一个整数,表示小朋友的不高兴程度和的最小值。
数据范围
1≤n≤100000,
0≤Hi≤1000000
输入样例:
3
3 2 1
输出样例:
9
样例解释
首先交换身高为3和2的小朋友,再交换身高为3和1的小朋友,再交换身高为2和1的小朋友,每个小朋友的不高兴程度都是3,总和为9。
解题思路
这道题就类似冒泡排序,每次交换逆序对,但是如果用冒泡排序,会超时,对于原数组的每一个数,它交换的次数取决于它前面有多少个数比它大和它后面有多少个数比它小,这两者的和就是每个数会交换的次数,而如何找出比每个数大的数和比每个数小的数,就可以借助树状数组,树状数组维护的是每个数出现的次数,下标表示的就是数,数组的值就是这个数出现的次数,比x小的数,就是tr[x-1],也就是从1~x-1这些数出现的和,比x大的数,就是所有数出现的次数减去1~x出现的次数,知道了交换的次数,就可以用等差数列公式求出不高兴程度
代码实现+详细注释 C++
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1000010;
int a[N],tr[N],sum[N];//树状数组维护的是每个数出现的次数 sum记录的是每个小朋友的移动次数
int lowbit(int x)
return x&-x;
void add(int x,int v)
for(int i=x;i<N;i+=lowbit(i)) tr[i]+=v;
int query(int x)
int res=0;
for(int i=x;i;i-=lowbit(i)) res+=tr[i];
return res;
int main()
int n;
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&a[i]),a[i]++;
//求每个数有多少个数比它大
for(int i=0;i<n;i++)
sum[i]=query(N-1)-query(a[i]);//也就是a[i]+1到N-1的个数
add(a[i],1);
memset(tr,0,sizeof(tr));
//求每个数有多少数比它小
for(int i=n-1;i>=0;i--)
sum[i]+=query(a[i]-1);
add(a[i],1);
long long res=0;
for(int i=0;i<n;i++) res+=(long long)sum[i]*(sum[i]+1)/2;//移动第1次加1,第2次加2,第sum[i]加sum[i],所以一共移动(1+2+...+sum[i]=sum[i]*(sum[i]+1)/2)
printf("%lld\\n",res);
return 0;
二、线段树
关于线段树
单点修改:递归加回溯 递归到某个点修改完之后回溯修改上一层,一直到最上面
区间查询:递归查找,如果要找的区间包含住线段树的这个区间,就加上这个区间的值返回,否则再递归下去
假设最后一层有n个点,上一层就是n/2,再往上n/4…1,加上有些层可能有的结点每一孩子,也要加上去,所以所有节点加起来小于等于4n
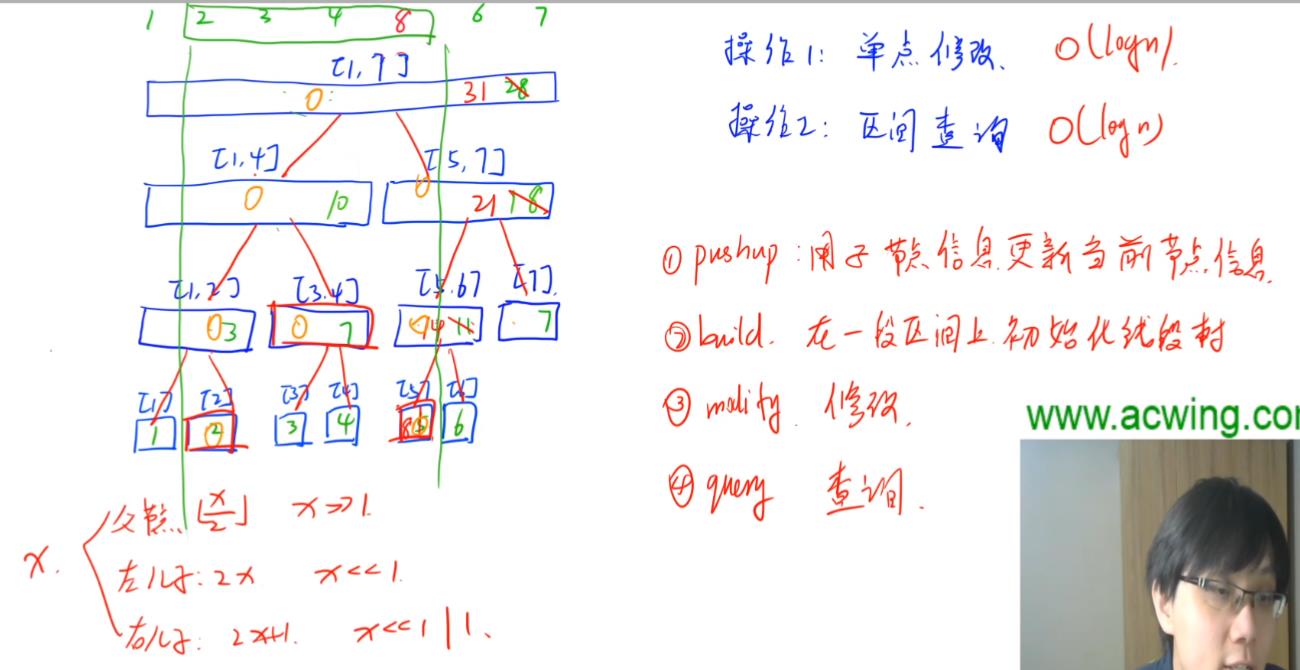
关于线段树的四个操作
void pushup(int u)//求结点u的区间和,就是u的左右孩子的和
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
void build(int u,int l,int r)//建立一个线段树,先递归到最后一层,再往上求父节点,一直到根节点
if(l==r) tr[u]=l,r,w[r];
else
tr[u]=l,r;
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
int query(int u,int l,int r)//查询l~r区间和,递归查询,直到要该区间被包含在要查询的区间内
if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
int mid=tr[u].l+tr[u].r>>1;
int sum=0;
if(l<=mid) sum=query(u<<1,l,r);
if(r>mid) sum+=query(u<<1|1,l,r);
return sum;
void modify(int u,int x,int v)//给x位置加上v,然后更新线段树
if(tr[u].l==tr[u].r) tr[u].sum+=v;
else
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
例题
1.动态求连续区间和
题目描述
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。
数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。
数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35
解题思路
这道题是模板题,直接用模板就行
代码实现+详细注释 C++
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=100010;
int w[N];
int n,m;
struct Node
int l,r;
int sum;
tr[N*4];
void pushup(int u)//通过子 求父,就是左右孩子的和
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
void build(int u,int l,int r)//建立一个线段树
if(l==r) tr[u]=l,r,w[l];
else
tr[u]=l,r;
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
int query(int u,int l,int r)//查询l~r区间的和
if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
int mid=tr[u].l+tr[u].r>>1;
int sum=0;
if(l<=mid) sum=query(u<<1,l,r);
if(r>mid) sum+=query(u<<1|1,l,r);
return sum;
void modify(int u,int x,int v)//给线段树x位置+v 更新线段树
if(tr[u].l==tr[u].r) tr[u].sum+=v;
else
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
int main()
int k,x,y;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
build(1,1,n);
while(m--)
cin>>k>>x>>y;
if(k==0) cout<<query(1,x,y)<<endl;
else modify(1,x,y);
return 0以上是关于2022蓝桥杯学习——5.树状数组和线段树差分的主要内容,如果未能解决你的问题,请参考以下文章