正值实系数多项式函数所对应的导数累加和是否非负?
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了正值实系数多项式函数所对应的导数累加和是否非负?相关的知识,希望对你有一定的参考价值。
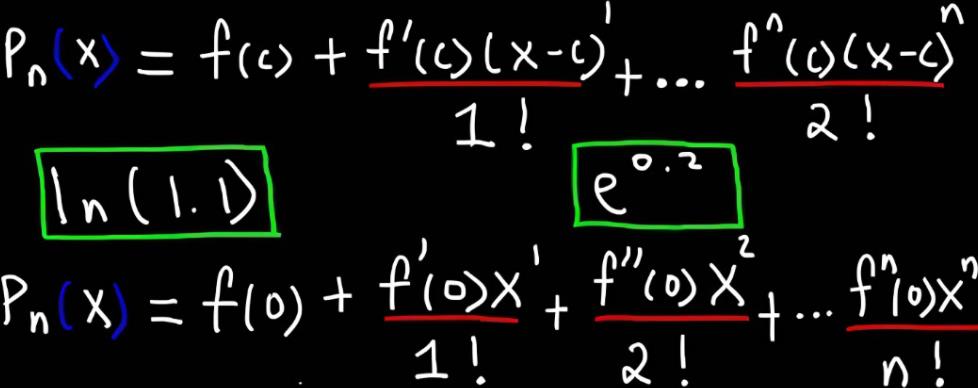
简 介: 对于多项式导数累计的性质证明,告诉我们数学的证明与工程上的证明是多么大的区别。这道微积分的考试题目让我思考了一整天,只有看到网络上的证明才会有感到恍然大悟的感觉。
这个证明太绝妙了。
关键词: 多项式,导数,非负
§01 题目来源
这个题目来自于博文 今年期末微积分考试试题:看看你能够在两个小时内做对几道题? 的第18题。
1.1 题目内容:
设:
p
(
x
)
=
x
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
1
x
+
a
0
p\\left( x \\right) = x^n + a_n - 1 x^n - 1 + \\cdots + a_1 x + a_0
p(x)=xn+an−1xn−1+⋯+a1x+a0 为实系数
n
n
n 次多项式。若
p
(
x
)
≥
0
,
x
∈
(
−
∞
,
+
∞
)
p\\left( x \\right) \\ge 0,\\,\\,x \\in \\left( - \\infty , + \\infty \\right)
p(x)≥0,x∈(−∞,+∞)
证明:
p
(
x
)
+
p
′
(
x
)
+
⋯
+
p
(
n
)
(
x
)
≥
0
,
x
∈
(
−
∞
,
+
∞
)
p\\left( x \\right) + p'\\left( x \\right) + \\cdots + p^\\left( n \\right) \\left( x \\right) \\ge 0,\\,\\,x \\in \\left( - \\infty , + \\infty \\right)
p(x)+p′(x)+⋯+p(n)(x)≥0,x∈(−∞,+∞)
这里
p
′
(
x
)
,
p
′
′
(
x
)
,
⋯
,
p
(
n
)
(
x
)
p'\\left( x \\right),p''\\left( x \\right), \\cdots ,p^\\left( n \\right) \\left( x \\right)
p′(x),p′′(x),⋯,p(n)(x)表示
p
(
x
)
p\\left( x \\right)
p(x)的一阶、二阶以及
n
n
n阶导数。
1.2 题目分析
能够满足上面多项式 p ( x ) p\\left( x \\right) p(x)要求的多项式的一个最简单的函数为二次函数:
p ( x ) = x 2 p\\left( x \\right) = x^2 p(x)=x2
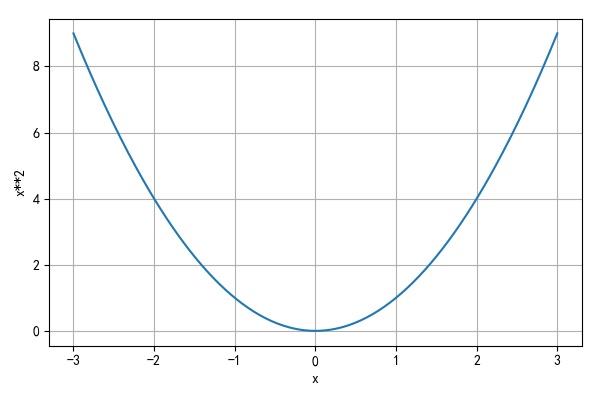
▲ 图1.2.1 p(x)的函数图像
那么:
p ( x ) + p ′ ( x ) + p ′ ′ ( x ) = x 2 + 2 x + 2 p\\left( x \\right) + p'\\left( x \\right) + p''\\left( x \\right) = x^2 + 2x + 2 p(x)+p′(x)+p′′(x)=x2+2x+2
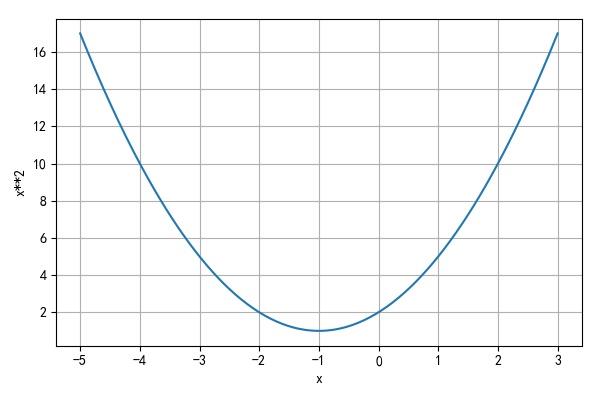
▲ x**2+2x+2函数图像
min(fx) = 1
可以看出它是满足条件所指定的情况。
甚至也可以验证当
p
(
x
)
=
x
4
p\\left( x \\right) = x^4
p(x)=x4时,对应的:
p
′
′
′
′
(
x
)
+
p
′
′
′
(
x
)
+
p
′
′
(
x
)
+
p
′
(
x
)
+
p
(
x
)
=
x
4
+
4
x
3
+
12
x
2
+
24
x
+
24
p''''\\left( x \\right) + p'''\\left( x \\right) + p''\\left( x \\right) + p'\\left( x \\right) + p\\left( x \\right) = x^4 + 4x^3 + 12x^2 + 24x + 24
p′′′′(x)+p′′′(x)+p′′(x)+p′(x)+< 以上是关于正值实系数多项式函数所对应的导数累加和是否非负?的主要内容,如果未能解决你的问题,请参考以下文章