随机过程 17 -离散时间马氏链典型应用

Posted 2022-02-06 Ciaran-byte

离散时间马尔科夫链的典型应用

文章目录

• 离散时间马尔科夫链的典型应用
• • 0. 概述
  • 1. Page Rank
  • • 1.1 背景
    • 1.2 模型建立
    • 1.3 模型求解
  • 2. MCMC
  • • 2.1 概述
    • 2.2 实现思路
    • 2.3 具体实现
    • • 2.3.1 第一步：细致平衡
      • 2.3.2 第二步：构成一步转移矩阵P
      • 2.3.3 第三步：运行马氏链
  • 3. 隐马尔科夫模型
  • • 3.1 概述
    • 3.2 计算隐马尔科夫模型观测数据的概率
    • • 3.2.1 直接计算方法
      • 3.2.2 前向递推
    • 3.3 计算状态的条件概率最大值

0. 概述

  这部分要讲解马尔科夫链排在前三的应用。

• Page Rank
• MCMC
• Hidden Markov

1. Page Rank

1.1 背景

$$\text{Google}$$

  PageRank是谷歌的核心技术。用于实现搜索引擎得到的网页重要性排序。

$$\text{Web Pages}\to \text{Page Ranking}\to \text{Searching}\to \text{Searching Engines}$$

  PageRank是1998-2000年由Brein和Page做出的工作

1.2 模型建立

  这可以看做是一个有向图求解极限转移概率的问题。之前讨论的是无向图的极限概率转移。

  对于无向图，只有度的概念，而有向图分成了入度和出度。

  之所以用有向图模型是因为，我们可以把网页看做是图的结点，把节点之间的连接，看做是网页之间的连接

$$\begin{gathered} \text{Web Pages}\to \text{Nodes of Graph} \\ \text{Link}\to \text{Edges of Graph} \end{gathered}$$

  一开始，人们考虑用入度来表示结点的重要性。因为如果一个网页很重要，必然会有很多的网站引用他。

$$\text{Importance}\iff \text{in degree}$$

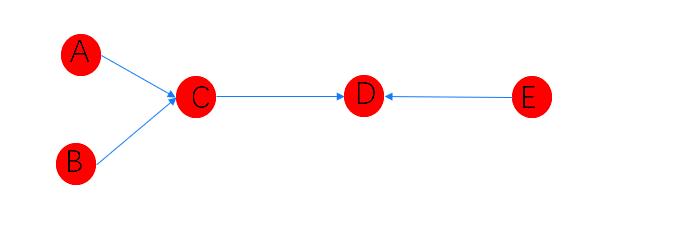
  但是只用入度来描述是不够的，因为这个有向图模型中C和D的入度都是2，但是可以看出来，D更加的重要。

  Brin和Page提出了自己的观点，认为网页节点的重要性应该等同于极限分布。当经过n步转移之后，各个节点被访问的情况就趋于平稳了，就能够判断哪个节点更加的重要了，就是访问节点次数除以总的访问次数。

$$\text{Importance}\iff \text{Limit Distribution}$$

  但是，求这个模型的极限分布是有问题的，因为这个概率转移矩阵很稀疏，只有个别点是有值的，大部分点是没有值的。因此会存在分布极限存在性问题，只有不可约+非周期才能够保证分布极限的存在。这个稀疏的矩阵这两点都难以保证。

  因此，Brin和Pgae的策略是，在原来的一步转移概率矩阵上做了调整，增加上一个全一矩阵，得到了一个新的一步转移概率矩阵。

$$\begin{gathered} \tilde{P}=(1-\alpha )P+\frac{\alpha }{n}\left(\begin{array}{ccc}1& ...& 1\\ ...& ...& ...\\ 1& ...& 1\end{array}\right) \\ \text{Google Matrix} \end{gathered}$$

  这个模型可以从这些角度进行分析

• 首先，这个做法是有实际意义的。因为有时候我们搜索网页不会是只在网页中存在的链接进行跳转，也会在地址栏中通过url进行跳转，即使两个网页之间没有直接联系，也是能够到达的,因此任意两个网页之间都有跳转概率。
• 加了新的矩阵之后，转移概率矩阵就是不可约的了。
• 加了新矩阵之后，任意两个点都是有连接关系的，因此各个状态一定都是非周期的。

1.3 模型求解

$$\pi =\pi \tilde{P}$$

  即求矩阵P的左特征值。

$$\text{Principal Left Eigenvector of }\tilde{P}\Rightarrow QR$$

  求特征值可以使用QR分解的方法

2. MCMC

2.1 概述

   MCMC是离散马尔科夫蒙特卡洛的缩写

$$\text{MCMC}\Rightarrow \text{Markov Chain Monte Carlo}$$

  蒙特卡洛技术是指，我们想要做某种仿真，仿真中有很多的随机效应，这样的随机效应一定是由某种随机变量描述的。

  这个随机变量的分布可以很简单，比如用高斯分布、均匀分布等模型来描述，这个分布也可能很复杂，可能是不连续的、不光滑的，即使知道了分布，也很那求均值。

  因为，我们很难通过分布来描述一个随机变量，最终就只能通过仿真而不是解析的方式来描述这些样本

$$\text{Simulation}\to \text{Random Effect}\to \text{Random Variables}\to \text{Distribution}\to \text{Simulation}$$

  所谓仿真，就是产生一组伪随机样本,这些伪随机样本可以产生某种分布

$$\begin{gathered} Generate{Z}_1,...,Z_n\sim f(x) \\ \text{Pseudo-Random Sample} \end{gathered}$$

  我们对这些分布并不了解，但是我们可以转化为对样本的研究。

  比如我们需要计算期望，但是积分非常难算，我们就可以用样本均值替代。

$$\begin{gathered} E(Z)={\int }_{-\infty }^{+\infty }xf(x)dx \\ \to \frac{1}{n}\sum _{k=1}^n{Z}_k \end{gathered}$$

  甚至我们可以通过直方图的方法，估计分布情况。

  如果我们有足够多的样本，甚至就不需要分布了，因为我们对分布没有办法进行解析计算。

  因此，蒙特卡洛模拟在随机变量仿真上，具有非常重要的地位。蒙特卡洛模拟由下面的人发明

• von Neumann 冯诺依曼
• Ulam
• Fermi

  蒙特卡洛的核心思想，就是把对分布的解析研究，转换为对样本的研究。

  具体目的是，如何做到，随便给一个分布，就能够得到服从这个分布的样本。

  蒙特卡洛的困难在于，有了样本是可以得到对分布的认知的，但是现在要做的是逆向操作，有了分布如何去获取样本

$$\begin{gathered} Z_1,...,Z_n\to f(x) \\ f(x)?\to Z_1,..,Z_n \end{gathered}$$

  同时，我们希望这种方法是通用的，一般来说，对某种具体的分布的采样策略是已知的，但是如果没有通用的策略，如果出现了一种新的分布，就没有办法进行仿真。

2.2 实现思路

$$\text{Universal Pseudo-Random Sampler}$$

  我们希望有一个通用的伪随机采样方法，能够得到任意分布的样本。

  马氏链是对这个问题最好的解决方案。P是一步转移概率矩阵。bi是初始分布。我们假设是不可约的，非周期的。

$$\begin{gathered} P=(P_{ij}{)}_{ij} \\ {b}_i=P(Z_0=i) \\ \text{Irreducible + Non-Perdic}\Rightarrow \pi =\pi P \end{gathered}$$

  现在我们假设极限分布是已知的，就是我们的目标分布。虽然目标分布可能是连续的，不过不本质，连续空间马氏链也有求解极限分布的方法。

  我们假设极限分布就是我们已知的需要采样的分布。然后我们反过来求一步转移概率矩阵。

  这是个非适定问题。因为P有n²个元素，π有n个元素，也就是用n个方程求解n²个未知数

  假如是能够求解到一步转移概率的话，就能产生随机样本了。因为马氏链的转移规律已经知道了，我们只需要让马氏链运行起来即可。然后抛弃前面的样本，因为前面的马氏链还没有收敛。然后每次run一步都能够得到一个样本轨道上的点，每一步都是服从样本分布的。

  这是迄今为止，最好的，通用的产生随机样本的方法。

2.3 具体实现

  需要分三步来求解。

2.3.1 第一步：细致平衡

$$\text{Detailed Balance}$$

  我们假设有极限分布π，还有一步转移概率P，我们要求解的方程如下

$$\begin{gathered} \pi =({\pi }_0,{\pi }_1,...,{\pi }_n)P=(P_{ij}{)}_{ij} \\ \pi =\pi P \end{gathered}$$

  但是这个方程不好验证，我们需要找一个充分条件，当满足充分条件的时候，这个方程成立。这个条件就叫做细致平衡

$${\pi }_i{P}_{ij}={\pi }_j{P}_{ji}\Rightarrow \pi =\pi QTP生成随机数字+字母$$

17 | 如何正确地显示随机消息？ 学习记录

python核心编程第五章练习-5.17-随机序列

Java基础17-随机数正则表达式

超简单的Python教程系列——第17篇：随机值

17 | 如何正确地显示随机消息？