目标检测中回归损失函数（L1Loss,L2Loss,Smooth L1Loss,IOU,GIOU,DIOU,CIOU,EIOU,αIOU ,SIOU)

Posted zyw2002

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了目标检测中回归损失函数（L1Loss,L2Loss,Smooth L1Loss,IOU,GIOU,DIOU,CIOU,EIOU,αIOU ,SIOU)相关的知识，希望对你有一定的参考价值。

文章目录

L-norm Loss 系列

L1 Loss

  • 别称
    L1范数损失、最小绝对误差（LAD）、平均绝对值误差（MAE）
  • 计算公式
    loss ⁡ ( x , y ) = 1 n ∑ i = 1 n ∣ y i − f ( x i ) ∣ \\operatornameloss(x, y)=\\frac1n \\sum_i=1^n\\left|y_i-f\\left(x_i\\right)\\right| loss(x,y)=n1​i=1∑n​∣yi​−f(xi​)∣
    其中 y i y_i yi​是真实值， f ( x i ) f(x_i) f(xi​)是预测值，n是样本点个数
  • 导数
    d L 1 ( x ) d x = 1  if  x ≥ 0 − 1  otherwise  \\frac\\mathrmd L_1(x)\\mathrmd x= \\begincases1 & \\text if x \\geq 0 \\\\ -1 & \\text otherwise \\endcases dxdL1​(x)​=1−1​ if x≥0 otherwise ​
  • 特性
    优点：无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解
    缺点：在中心点是折点，不能求导，梯度下降时要是恰好学习到w=0就没法接着进行了
    L 1 L_1 L1​损失函数对 x 的导数为常数，训练后期，x 很小时，如果学习率不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。

L2 Loss

  • 公式
    L 2 = ∑ i = 1 n ( y i − f ( x i ) ) 2 L 2=\\sum_i=1^n\\left(y_i-f\\left(x_i\\right)\\right)^2 L2=i=1∑n​(yi​−f(xi​))2
  • 导数
    d L 2 ( x ) d x = 2 x \\frac\\mathrmd L_2(x)\\mathrmd x=2 x dxdL2​(x)​=2x
  • 特性
    L2 loss由于是平方增长，因此学习快。L2损失函数对 x 的导数为2x，当 x 很大的时候，导数也很大，使L2损失 在 总loss 中占据主导位置，进而导致，训练初期不稳定。

Smooth L1 Loss

《Fast R-CNN》 论文中首次提出Smooth L1 Loss

  • 公式
    smooth ⁡ L 1 ( x ) = 0.5 x 2  if  ∣ x ∣ < 1 ∣ x ∣ − 0.5  otherwise  \\operatornamesmooth_L_1(x)= \\begincases0.5 x^2 & \\text if |x|<1 \\\\ |x|-0.5 & \\text otherwise \\endcases smoothL1​​(x)=0.5x2∣x∣−0.5​ if ∣x∣<1 otherwise ​
    其中 x = y i − f ( x i ) x=y_i-f(x_i) x=yi​−f(xi​)
  • 导数
    d smooth ⁡ L 1   d x = x  if  ∣ x ∣ < 1 ± 1  otherwis  \\frac\\mathrmd \\operatornamesmooth_L_1\\mathrm~d x= \\begincasesx & \\text if |x|<1 \\\\ \\pm 1 & \\text otherwis \\endcases  dxdsmoothL1​​​=x±1​ if ∣x∣<1 otherwis ​
  • 特性
    分析一下，当预测值f(xi)和真实值yi差别较小的时候（绝对值差小于1），其实使用的是L2 loss；差别大的时候，使用的是L1 loss的平移。因此，Smooth L1 loss其实是L1 loss 和L2 loss的结合，同时拥有两者的部分优点：
    真实值和预测值差别较小时（绝对值差小于1），梯度也会比较小（损失函数比普通L1 loss在此处更圆滑）
    真实值和预测值差别较大时，梯度值足够小（普通L2 loss在这种位置梯度值就很大，容易梯度爆炸）

IOU系列

IOU （2016）

论文地址： 《UnitBox: An Advanced Object Detection Network》

  • 提出背景
    三种Loss用于计算目标检测的Bounding Box Loss时，独立的求出4个点的Loss，然后进行相加得到最终的Bounding Box Loss，这种做法的假设是4个点是相互独立的，实际是有一定相关性的

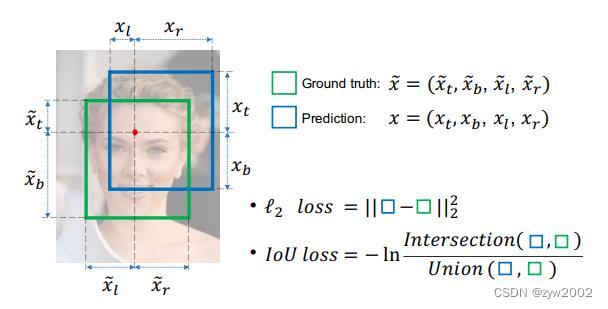
  • IoU (Intersection over Union)的计算
    IOU的计算是用预测框(A)和真实框(B)的交集除以二者的并集，其公式为：
    I o U = A ∩ B A ∪ B I o U=\\fracA \\cap BA \\cup B IoU=A∪BA∩B​
    IoU的值越高也说明A框与B框重合程度越高，代表模型预测越准确。反之，IoU越低模型性能越差。

  • IOU Loss
    L I o U = − l n ( I o U ) L_IoU=-ln(IoU) LIoU​=−ln(IoU)
    当IoU趋近为1时（两个框重叠程度很高），Loss趋近于0。IoU越小(两个框的重叠程度变低)，Loss越大。当IoU为0时（两个框不存在重叠），梯度消失。

  • IOU的特性
    优点：
    （1）IoU具有尺度不变性
    （2）结果非负，且范围是(0, 1)
    缺点：
    （1）如果两个目标没有重叠，IoU将会为０,并且不会反应两个目标之间的距离，在这种无重叠目标的情况下，如果IoU用作于损失函数，梯度为０，无法优化。
    （2）IoU无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

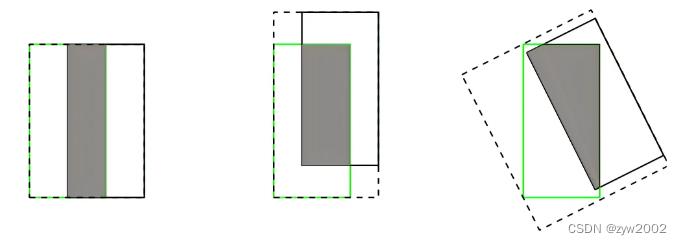
GIOU （2019）

论文地址：《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》

  • 提出背景
    为了解决Iou的作为损失函数的缺点，提出了GIoU，在IoU后面增加了一项，计算两个框的最小外接矩形，用于表征两个框的距离，从而解决了两个目标没有交集时梯度为零的问题。

  • GIOU的计算
    其中A表示真实框，B表示预测框，C表示两个框的最小外接矩形的面积。
    G I o U = I o U − C − ( A ∪ B ) C G I o U=I o U-\\fracC-(A \\cup B)C GIoU=IoU−CC−(A∪B)​
    当IoU=0时（A和B没有交集）：
    G I o U = − 1 + A ∪ B C G I o U=-1+\\fracA \\cup BC GIoU=−1+CA∪B​
    当A和B两个框离得越远，GIOU越接近-1；当两框重合时，GIOU=1。所以GIOU的取值为(-1,1]。

  • GIOU Loss
    L G I o U = 1 − G I o U L_G I o U=1-G I o U LGIoU​=1−GIoU
    当 A , B A,B A,B两框不相交时， A ∪ B A \\cup B A∪B 不变，最大化 G I o U GIoU GIoU就是最小化C, 这样会促进两个框不断靠近。

  • GIoU的特性
    优点：
    （1）当IoU=0时，仍然可以很好的表示两个框的距离。
    （2）GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度
    缺点：
    （1）当两个框属于包含关系时，GIoU会退化成IoU，无法区分其相对位置关系，如下图：

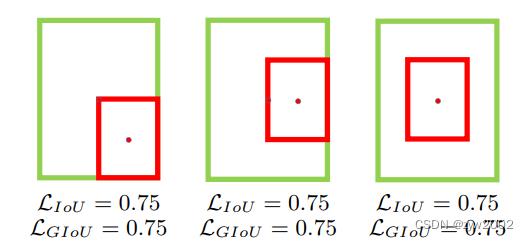
    （2）由于GIoU仍然严重依赖IoU，因此在两个垂直方向，误差很大，很难收敛。两个框在相同距离的情况下，水平垂直方向时，此部分面积最小，对loss的贡献也就越小，从而导致在垂直水平方向上回归效果较差。
    如下图，三种情况下GIoU的值一样，GIoU将很难区分这种情况。

DIOU （2020）

论文地址：《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》

  • 提出背景

针对上述GIoU的两个问题，将GIoU中最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程，这就诞生了DIoU。
DIoU要比GIou更加符合目标框回归的机制，将目标与预测之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。