：排序算法 -- 排序算法介绍和分类算法的时间效率（时间频度和时间复杂度）算法的稳定性

Posted 2022-02-04 CodeJiao

1. 排序算法介绍和分类

---

1.1 排序算法介绍

排序也称之为排序算法（Sort Algorithm），是讲一组数据以指定的顺序进行排列的过程。

---

1.2 排序算法分类

• 内部排序：将所有的数据都加载到内部存储器上进行排序。
• 外部排序：数据量多大，无法全部加载到内存中，需要借助外部存储（文档）进行排序。

算法分类图：

---

2. 算法的时间效率

• 事后统计方法：这种方法可行，但是存在于两个问题：一是要想对设计的算法运行性能进行评测就需要实际去运行该程序，而是所得时间统计量依赖于计算机硬件、软件等因素，这种方式要在同一台计算机的相同状态下运行，才能比较出哪一个算法速度更快，更好。

• 事前估算方法：通过分析某一个算法的时间复杂度来判断哪个算法更优，更好。

---

2.1 时间频度

时间频度：一个算法花费的时间与算法中语句的执行次数成正比，哪一个算法中语句执行次数多，那么他所花费的时间就会多。 一个算法中语句执行次数称之为语句频度或时间频度。记为T(n)。

int sum = 0;
for(int i=1;i<=n;i++)
  sum+=i;

当n = 100的时候，T(n) = n+1= 101，即100次循环加上第101次的判断（i = 101 的时候又会去判断一次）。

---

2.1.1 忽略常数项

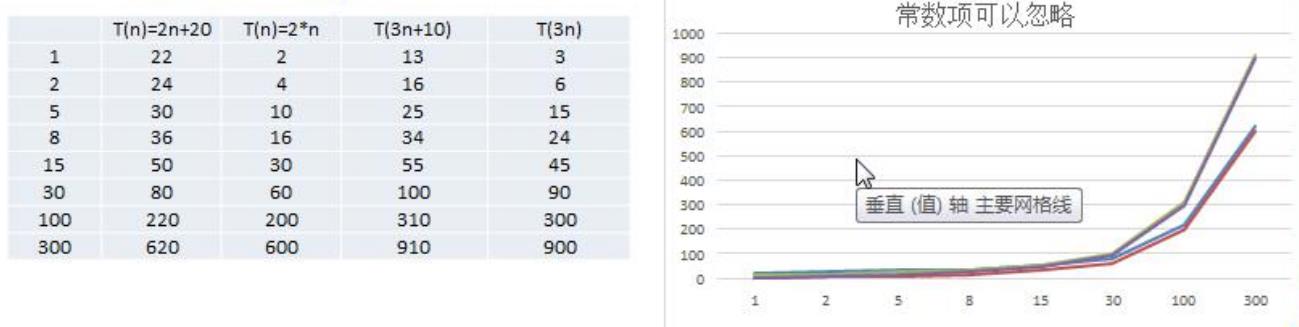
结论：

1. 2n+20 和 2n随着n变大，执行曲线无线接近，20可以忽略
2. 3n+10 和 3n随着n变大，执行曲线无限接近，10可以忽略

---

2.1.2 忽略低次项

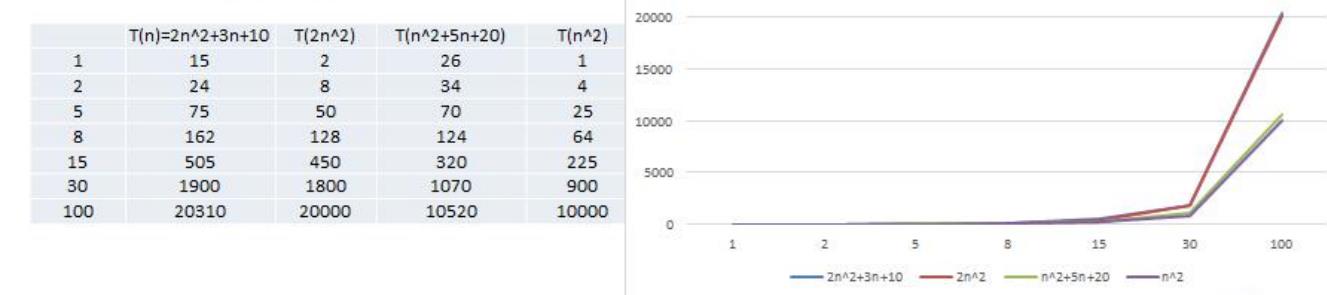
结论：

1. 2n^2+3n+10 和 2n^2 随着n变大，执行曲线无线接近，可以忽略3n+10
2. n^2+5n+20 和 n^2 随着n变大，执行曲线无线接近，可以忽略5n+20

---

2.1.3 忽略系数

结论：

• 随着n值变大，5n^2+7n 和 3n^2+2n 执行区间重合，说明这种情况下5和3可以忽略
• 而n^3+5n和6n^3+4n执行区间分离，说明多少次方式关键

---

2.2 时间复杂度

在计算机科学中，时间复杂性，又称时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，渐近时间复杂度又称之为时间复杂度。

---

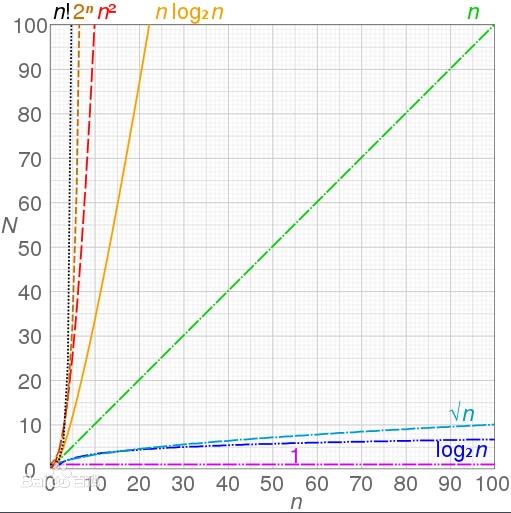
2.2.1 常见的时间复杂度

常数时间复杂度：

若对于一个算法，的上界与输入大小无关，则称其具有常数时间，记作O(1)时间T(n) =1

对数时间：

若算法的T(n) =O(logn)，则称其具有对数时间。

int I = 1;
while(i<n)
 i=i*2;


对于：x=log2^n   O(log2n)

幂对数时间：

对于某个常数k，若算法的T(n) = O((logn))，则称其具有幂对数时间

线性时间：

如果一个算法的时间复杂度为O(n)，则称这个算法具有线性时间，或O(n)时间。

for(i=1;i<=n;++i)
    j=I;
	j++;

线性对数时间：

若一个算法时间复杂度T(n) = O(nlog n)，则称这个算法具有线性对数时间。

指数时间：

例如O(n^2)，比如双层for循环。

---

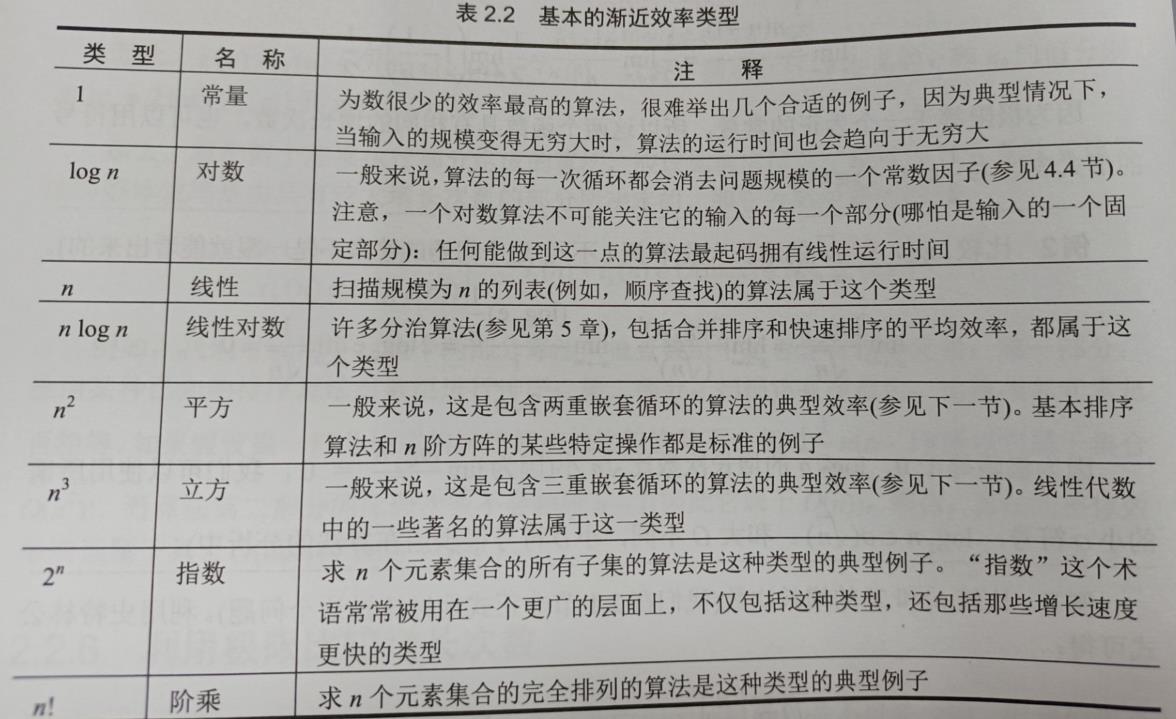
2.2.2 常见的时间复杂度对应图

---

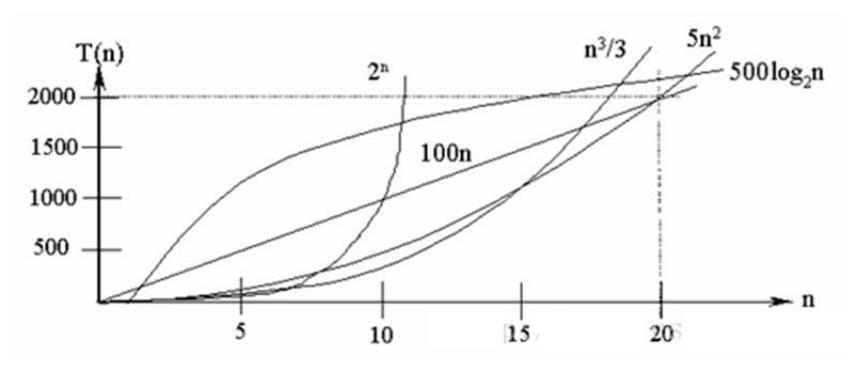
2.2.3 结论：

常见的算法时间复杂度由小到大依次为：

---

2.2.3 说明

尽可能的避免使用指数阶的算法

---

2.3 平均和最坏时间复杂度

平均时间复杂度：指所有可能的输入实例均以等概率的出现情况下得到算法的运行时间。

最坏时间复杂度：一般讨论的时间复杂度均是最坏情况下的时间复杂度，这样做的原因是最坏情况下的时间复杂度是算法在任何输入实例上运行的界限，这就保证了算法的运行时间不会比最坏情况更长。

平均时间复杂度和最坏时间复杂度是否一样，这就需要根据算法不同而不同了。

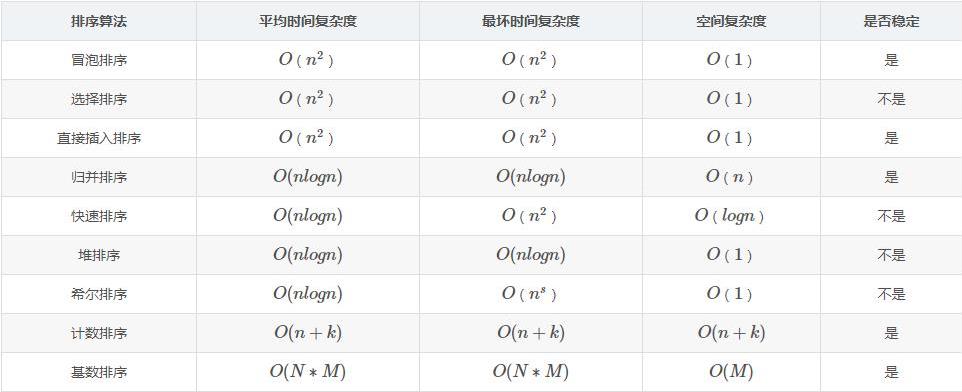
补充：算法的稳定性

算法稳定性指的是在一组待排序记录中，如果存在任意两个相等的记录R和S，且在待排序记录中R在S前，如果在排序后R依然在S前，即它们的前后位置在排序前后不发生改变，则称为排序算法为稳定的。

---

---