第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 ARIMAAutoARIMALSTMProphet多元Prophet 实现

Posted 2023-03-08 Better Bench

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 ARIMAAutoARIMALSTMProphet多元Prophet 实现相关的知识，希望对你有一定的参考价值。

完整代码下载链接

https://www.betterbench.top/#/35/detail

1 读取数据预处理的文件

import numpy as np
import pandas as pd

import seaborn as sns 
import matplotlib.pyplot as plt 
from colorama import Fore

from sklearn.metrics import mean_absolute_error, mean_squared_error
import math

import warnings # Supress warnings 
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
np.random.seed(7)

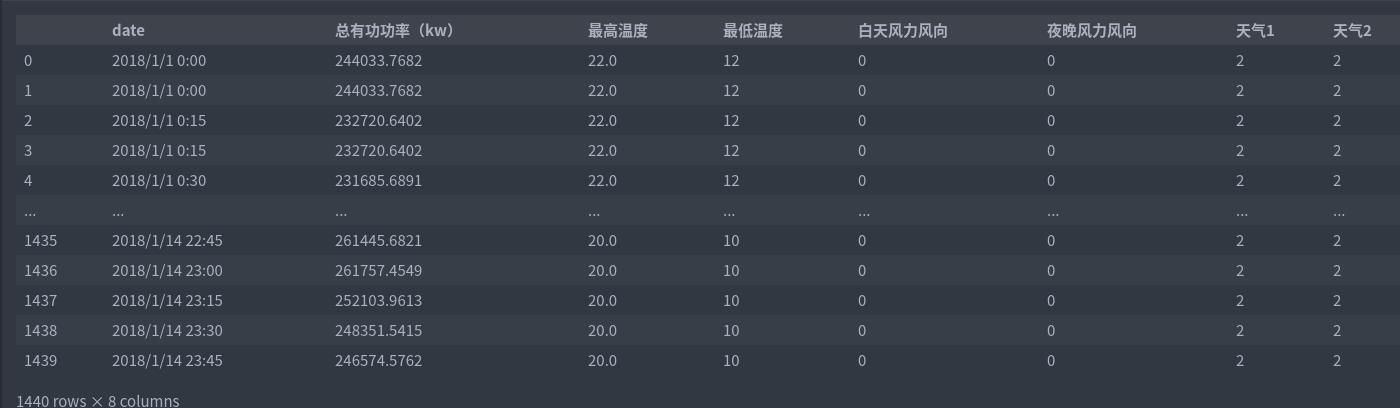
df = pd.read_csv(r"./data/泰迪杯数据2.csv")
df.head()

df  = df.rename(columns='日期1':'date')
df

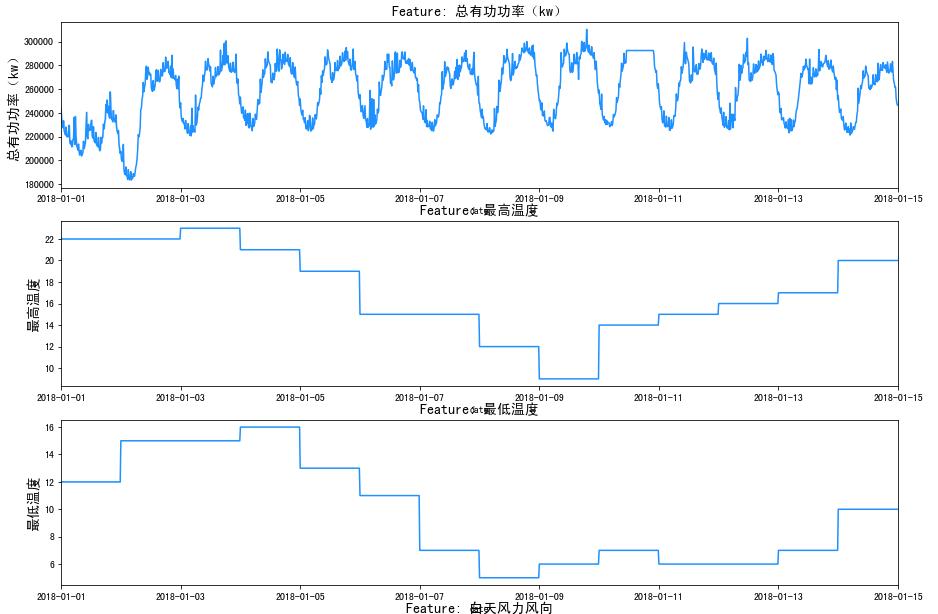
2 查看时序

from datetime import datetime, date 

df['date'] = pd.to_datetime(df['date'])
df.head().style.set_properties(subset=['date'], **'background-color': 'dodgerblue')

# To compelte the data, as naive method, we will use ffill
f, ax = plt.subplots(nrows=7, ncols=1, figsize=(15, 25))


for i, column in enumerate(df.drop('date', axis=1).columns):
  。。。略

df = df.sort_values(by='date')

# Check time intervals
df['delta'] = df['date'] - df['date'].shift(1)

df[['date', 'delta']].head()

df['delta'].sum(), df['delta'].count()

(Timedelta(‘13 days 23:45:00’), 1439)

df = df.drop('delta', axis=1)
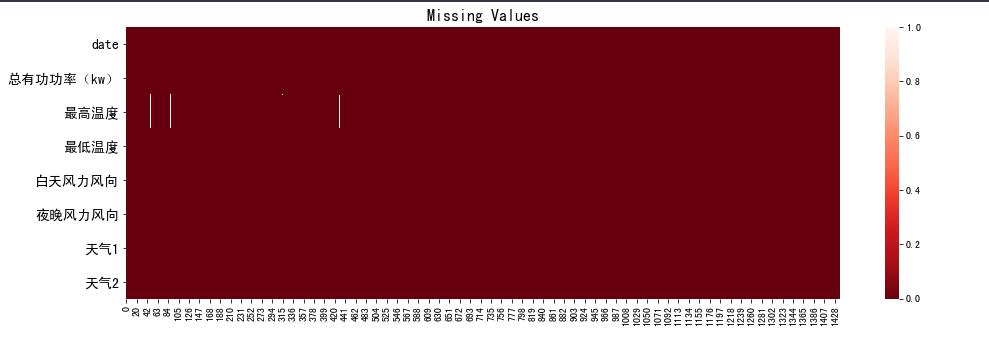
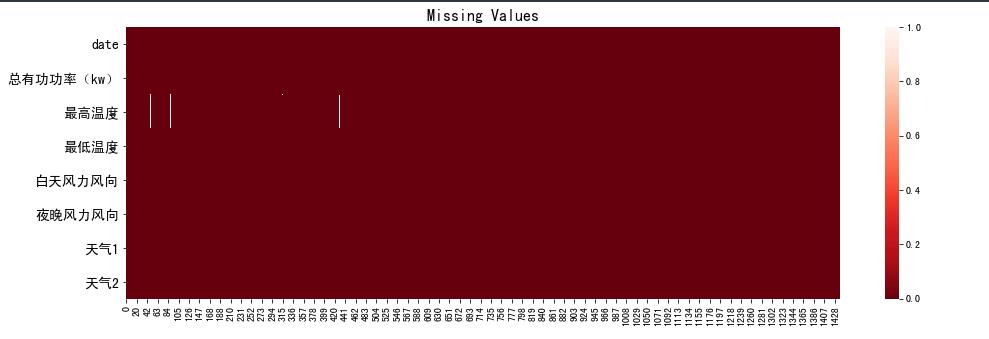
df.isna().sum()

date 0
总有功功率（kw） 51
最高温度 6
最低温度 0
白天风力风向 0
夜晚风力风向 0
天气1 0
天气2 0
dtype: int64

3 异常值缺失值

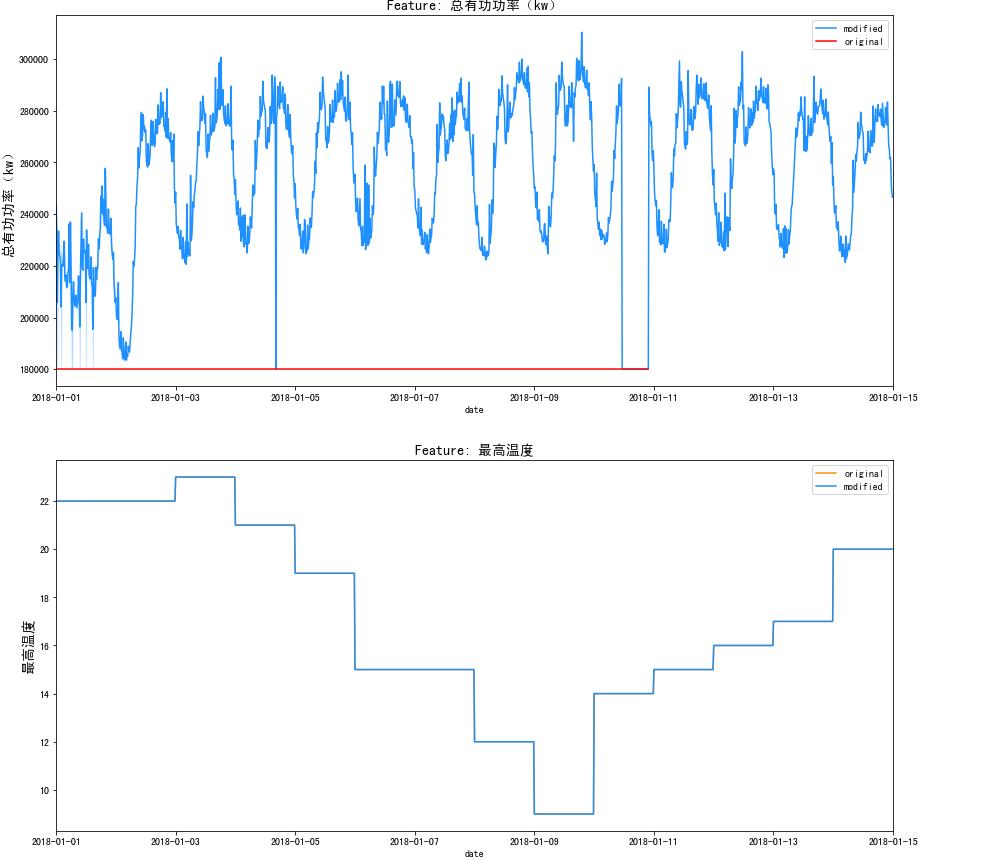
f, ax = plt.subplots(nrows=2, ncols=1, figsize=(15, 15))

。。。略


ax[1].set_xlim([date(2018, 1, 1), date(2018, 1, 15)])

3.1 HeatMap颜色

Accent, Accent_r, Blues, Blues_r, BrBG, BrBG_r, BuGn, BuGn_r,

BuPu, BuPu_r, CMRmap, CMRmap_r, Dark2, Dark2_r, GnBu, GnBu_r,

Greens, Greens_r, Greys, Greys_r, OrRd, OrRd_r,

Oranges, Oranges_r, PRGn, PRGn_r, Paired, Paired_r, Pastel1, Pastel1_r, Pastel2, Pastel2_r,

PiYG, PiYG_r, PuBu, PuBuGn, PuBuGn_r, PuBu_r, PuOr, PuOr_r, PuRd, PuRd_r, Purples, Purples_r,

RdBu, RdBu_r, RdGy, RdGy_r, RdPu, RdPu_r, RdYlBu, RdYlBu_r, RdYlGn, RdYlGn_r, Reds, Reds_r,

Set1, Set1_r, Set2, Set2_r, Set3, Set3_r, Spectral, Spectral_r, Wistia, Wistia_r, YlGn, YlGnBu,

YlGnBu_r, YlGn_r, YlOrBr, YlOrBr_r, YlOrRd, YlOrRd_r, afmhot, afmhot_r, autumn, autumn_r, binary,

binary_r, bone, bone_r, brg, brg_r, bwr, bwr_r, cividis, cividis_r, cool, cool_r, coolwarm,

coolwarm_r, copper, copper_r, cubehelix, cubehelix_r, flag, flag_r, gist_earth, gist_earth_r,

gist_gray, gist_gray_r, gist_heat, gist_heat_r, gist_ncar, gist_ncar_r, gist_rainbow,

gist_rainbow_r, gist_stern, gist_stern_r, gist_yarg, gist_yarg_r, gnuplot, gnuplot2,

gnuplot2_r, gnuplot_r, gray, gray_r, hot, hot_r, hsv, hsv_r, icefire, icefire_r, inferno,

inferno_r, jet, jet_r, magma, magma_r, mako, mako_r, nipy_spectral, nipy_spectral_r,

ocean, ocean_r, pink, pink_r, plasma, plasma_r, prism, prism_r, rainbow, rainbow_r,

rocket, rocket_r, seismic, seismic_r, spring, spring_r, summer, summer_r, tab10, tab10_r,

tab20, tab20_r, tab20b, tab20b_r, tab20c, tab20c_r, terrain, terrain_r, twilight, twilight_r,

twilight_shifted, twilight_shifted_r, viridis, viridis_r, vlag, vlag_r, winter, winter_r

f, ax = plt.subplots(nrows=1, ncols=1, figsize=(16,5))

sns.heatmap(df.T.isna(), cmap='Reds_r')
ax.set_title('Missing Values', fontsize=16)

for tick in ax.yaxis.get_major_ticks():
    tick.label.set_fontsize(14)
plt.show()

3.2 缺失值处理（多种填充方式）

f, ax = plt.subplots(nrows=4, ncols=1, figsize=(15, 12))

sns.lineplot(x=df['date'], y=df['总有功功率（kw）'].fillna(0), ax=ax[0], color='darkorange', label = 'modified')
sns.lineplot(x=df['date'], y=df['总有功功率（kw）'].fillna(np.inf), ax=ax[0], color='dodgerblue', label = 'original')
ax[0].set_title('Fill NaN with 0', fontsize=14)
ax[0].set_ylabel(ylabel='Volume', fontsize=14)

。。。略

for i in range(4):
    ax[i].set_xlim([date(2018, 1, 1), date(2018, 1, 15)])
    
plt.tight_layout()
plt.show()

df['总有功功率（kw）'] = df['总有功功率（kw）'].interpolate()

4 数据平滑与采样

重采样可以提供数据的附加信息。有两种类型的重采样:

上采样是指增加采样频率(例如从几天到几小时)

下采样是指降低采样频率(例如，从几天到几周)

在这个例子中，我们将使用。resample()函数

fig, ax = plt.subplots(ncols=1, nrows=3, sharex=True, figsize=(16,12))

sns.lineplot(df['date'], df['总有功功率（kw）'], color='dodgerblue', ax=ax[0])
ax[0].set_title('总有功功率（kw） Volume', fontsize=14)

。。。略
for i in range(3):
    ax[i].set_xlim([date(2018, 1, 1), date(2018, 1, 14)])

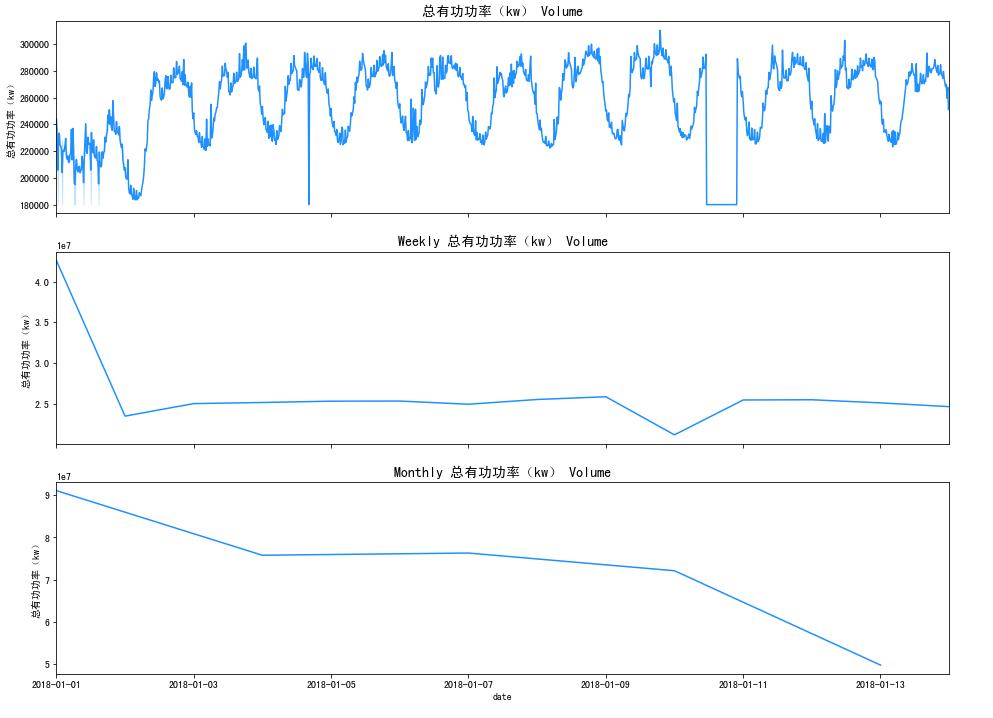
# As we can see, downsample to weekly could smooth the data and hgelp with analysis
downsample = df[['date',
                 '总有功功率（kw）', 
                ]].resample('7D', on='date').mean().reset_index(drop=False)

# df = downsample.copy()
downsample

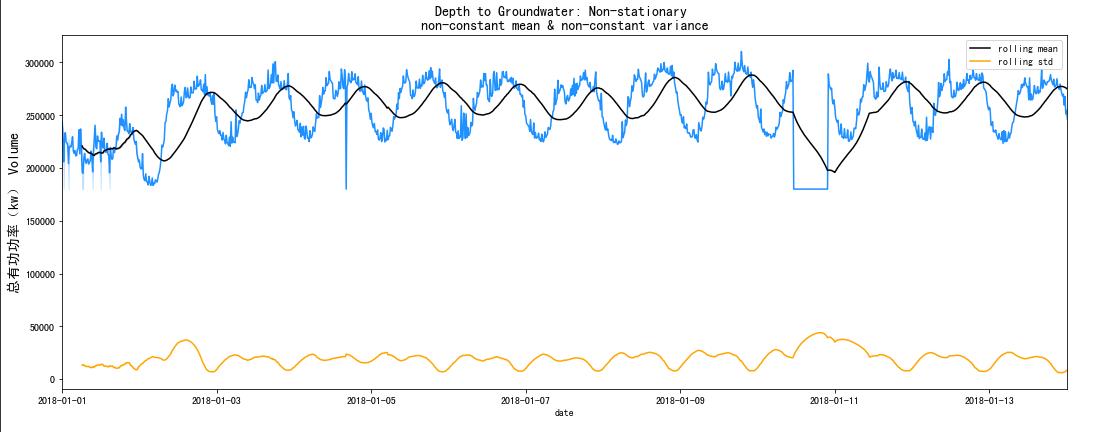
5 平稳性检验

目测:绘制时间序列并检查趋势或季节性

基本统计:分割时间序列并比较每个分区的平均值和方差

统计检验:增强的迪基富勒检验

# A year has 52 weeks (52 weeks * 7 days per week) aporx.
rolling_window = 52
f, ax = plt.subplots(nrows=1, ncols=1, figsize=(15, 6))

。。。略
plt.show()

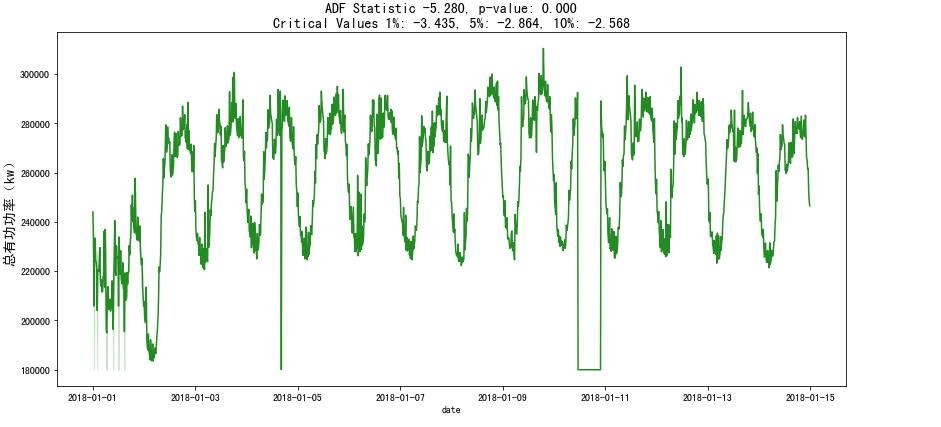
现在，我们将检查每个变量: p值小于0.05 检查ADF统计值与critical_values的比较范围

from statsmodels.tsa.stattools import adfuller

result = adfuller(df['总有功功率（kw）'].values)
result

(-5.279986646245767, 6.0232754503160645e-06, 24, 1415,

‘1%’: -3.434979825137732, ‘5%’: -2.8635847436211317, ‘10%’: -2.5678586114197954, 29608.16365155926)

# Thanks to https://www.kaggle.com/iamleonie for this function!
f, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 6))

def visualize_adfuller_results(series, title, ax):
   。。。略

visualize_adfuller_results(df['总有功功率（kw）'].values, '总有功功率（kw）',ax=ax)
# visualize_adfuller_results(df['temperature'].values, 'Temperature', ax[1, 0])
# visualize_adfuller_results(df['river_hydrometry'].values, 'River_Hydrometry', ax[0, 1])
# visualize_adfuller_results(df['drainage_volume'].values, 'Drainage_Volume', ax[1, 1])
# visualize_adfuller_results(df['depth_to_groundwater'].values, 'Depth_to_Groundwater', ax[2, 0])

# f.delaxes(ax[2, 1])
plt.tight_layout()
plt.show()

如果数据不是静态的，但我们想使用一个模型，如ARIMA(需要这个特征)，数据必须转换。

将序列转换为平稳序列的两种最常见的方法是:

变换:例如对数或平方根，以稳定非恒定方差

差分:从以前的值中减去当前值

6 数据转换

（1）对数

df['总有功功率（kw）_log'] = np.log(abs(df['总有功功率（kw）']))

。。。略
sns.distplot(df['总有功功率（kw）_log'], ax=ax[1])

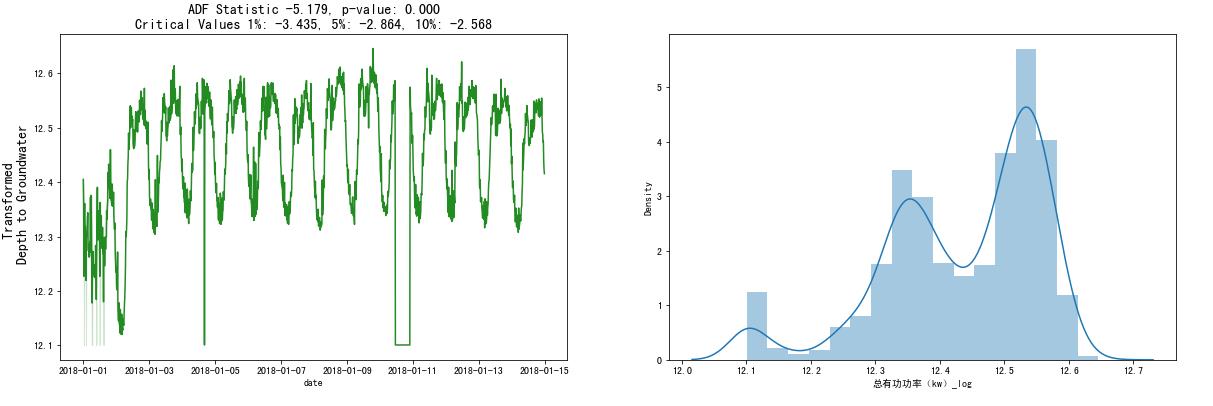
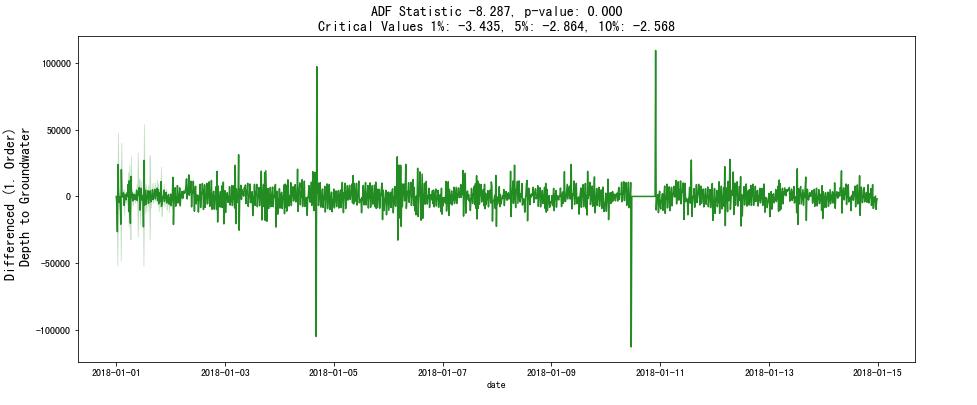
（2）一阶差分

# First Order Differencing
ts_diff = np.diff(df['总有功功率（kw）'])
df['总有功功率（kw）_diff_1'] = np.append([0], ts_diff)

f, ax = plt.subplots(nrows=1, ncols=1, figsize=(15, 6))
visualize_adfuller_results(df['总有功功率（kw）_diff_1'], 'Differenced (1. Order) \\n Depth to Groundwater', ax)

7 特征工程

7.1 时序提取

df['year'] = pd.DatetimeIndex(df['date']).year
df['month'] = pd.DatetimeIndex(df['date']).month
df['day'] = pd.DatetimeIndex(df['date']).day
。。。略

df[['date', 'year', 'month', 'day', 'day_of_year', 'week_of_year', 'quarter', 'season']].head()

7.2 编码循环特征

f, ax = plt.subplots(nrows=1, ncols=1, figsize=(20, 3))

sns.lineplot(x=df['date'], y=df['month'], color='dodgerblue')
ax.set_xlim([date(2018, 1, 1), date(2018, 1, 14)])
plt.show()

month_in_year = 12
df['month_sin'] = np.sin(2*np.pi*df['month']/month_in_year)
df['month_cos'] = np.cos(2*np.pi*df['month']/month_in_year)

f, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 6))

sns.scatterplot(x=df.month_sin, y=df.month_cos, color='dodgerblue')
plt.show()

7.3 时间序列分解

from statsmodels.tsa.seasonal import seasonal_decompose

core_columns =  [
    '总有功功率（kw）']
。。。略

fig, ax = plt.subplots(ncols=2, nrows=4, sharex=True, figsize=(16,8))

for i, column in enumerate(['总有功功率（kw）', '最低温度']):
    
    res = seasonal_decompose(df[column], freq=52, model='additive', extrapolate_trend='freq')

    ax[0,i].set_title('Decomposition of '.format(column), fontsize=16)
    res.observed.plot(ax=ax[0,i], legend=False, color='dodgerblue')
    ax[0,i].set_ylabel('Observed', fontsize=14)
。。。略

plt.show()

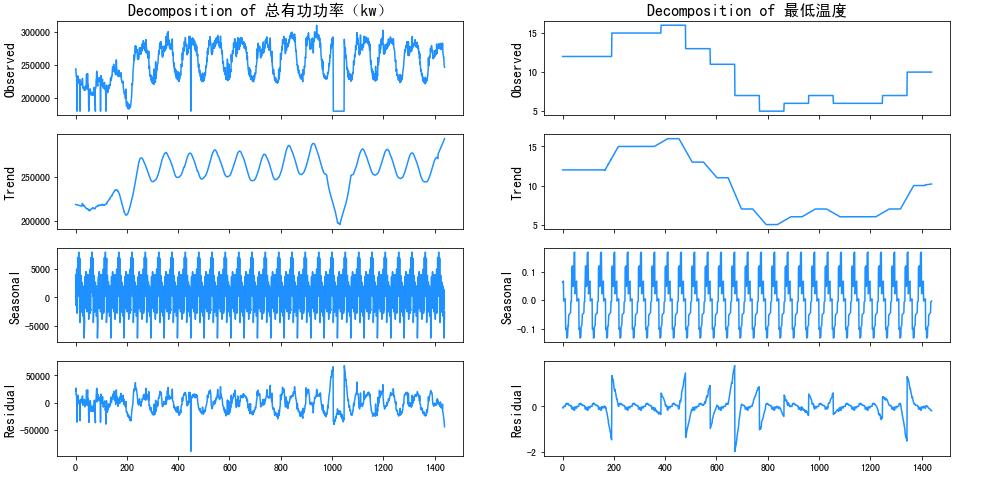
7.4 滞后特征

weeks_in_month = 4

for column in core_columns:
    df[f'column_seasonal_shift_b_2m'] = df[f'column_seasonal'].shift(-2 * weeks_in_month)
    df[f'column_seasonal_shift_b_1m'] = df[f'column_seasonal'].shift(-1 * weeks_in_month)
    df[f'column_seasonal_shift_1m'] = df[f'column_seasonal'].shift(1 * weeks_in_month)
    df[f'column_seasonal_shift_2m'] = df[f'column_seasonal'].shift(2 * weeks_in_month)
    df[f'column_seasonal_shift_3m'] = df[f'column_seasonal'].shift(3 * weeks_in_month)

7.6 探索性数据分析

f, ax = plt.subplots(nrows=1, ncols=1, figsize=(15, 6))
f.suptitle('Seasonal Components of Features', fontsize=16)

for i, column in enumerate(core_columns):
    。。。略
    
plt.tight_layout()
plt.show()

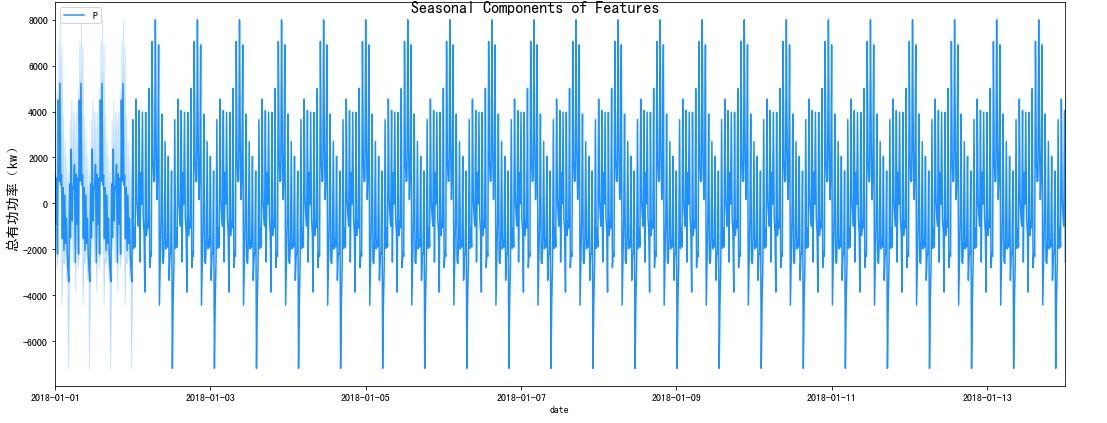
7.7 相关性分析

f, ax = plt.subplots(nrows=1, ncols=1, figsize=(8, 8))

。。。略

plt.tight_layout()
plt.show()

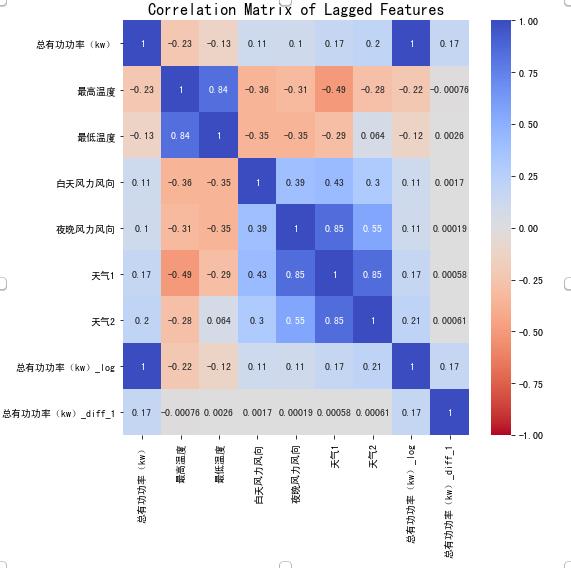
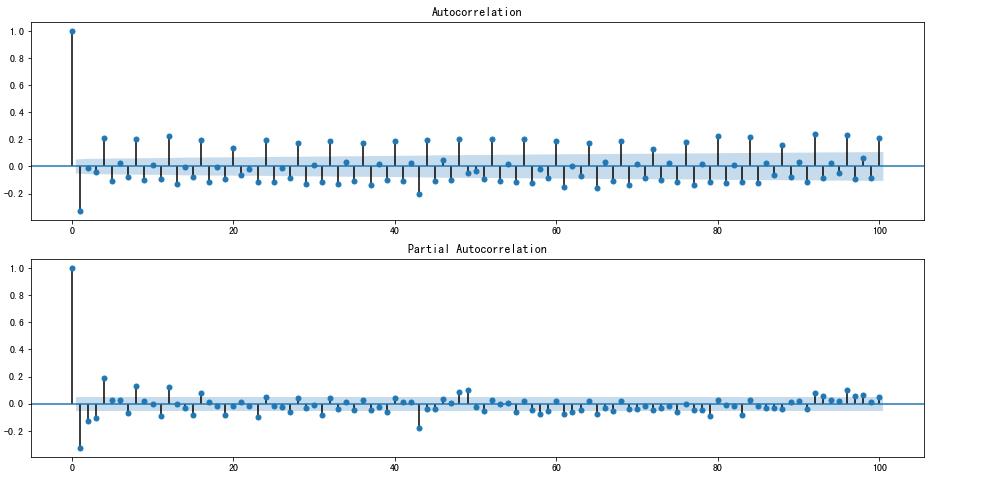
7.8 自相关分析

from pandas.plotting import autocorrelation_plot

autocorrelation_plot(df['总有功功率（kw）_diff_1'])
plt.show()

from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf

f, ax = plt.subplots(nrows=2, ncols=1, figsize=(16, 8))
。。。略

plt.show()

8 建模

8.1 时序中交叉验证

第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 问题二 时间突变分析 Python实现
 第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 ARIMAAutoARIMALSTMProphet多元Prophet 实现
 第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 Baseline
 第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 Baseline
 第十届“泰迪杯”数据挖掘挑战赛B题：电力系统负荷预测分析 ARIMAAutoARIMALSTMProphet多元Prophet 实现
 第十届泰迪杯数据挖掘大赛B题电力系统负荷预测时间突变检测