神经网络中的激活函数

Posted 2023-03-07 1 + 1=王

文章目录

• 为什么要使用激活函数
• 常用的激活函数
• 如何选择激活函数
• ReLU激活函数的优点及局限性
• 为什么Sigmoid和Tanh会导致梯度消失的问题
• 为什么Tanh收敛速度⽐Sigmoid快？

为什么要使用激活函数

在真实情况中，我们往往会遇到线性不可分问题，需要非线性变换对数据的分布进行重新映射。对于深度神经网络，我们在每一层线性变换后叠加一个非线性激活函数， 以避免多层网络等效于单层线性函数，从而获得更强大的学习与拟合能力。

常用的激活函数

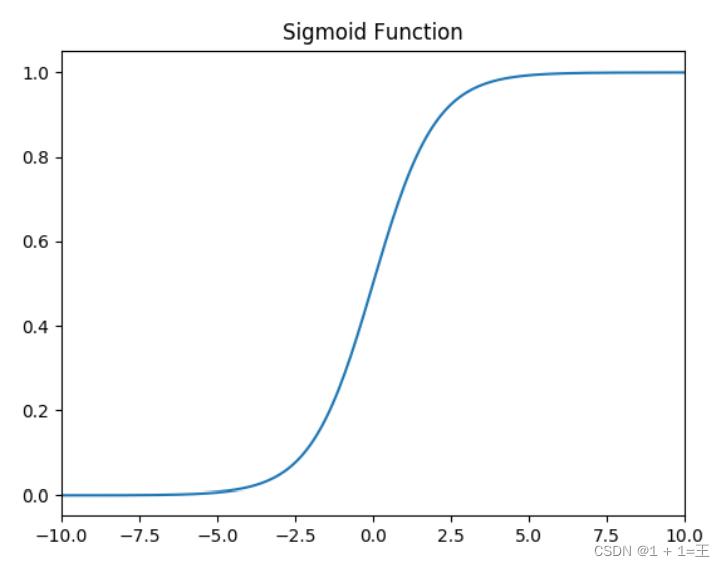
• Sigmoid函数
  
  

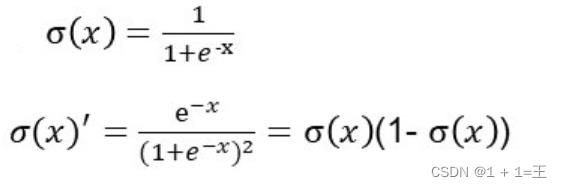
• Tanh函数
  

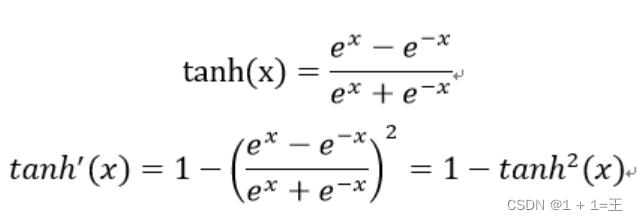
• ReLU函数

f(x) = max(0, x)

如何选择激活函数

1. 如果输出是⼆分类问题，则输出层选择 sigmoid 函数，然后其它的所有单元都选择 Relu 函数。
2. 如果在隐藏层上不确定使⽤哪个激活函数，那么通常会使⽤ Relu 激活函数。
3. sigmoid 激活函数：除了输出层是⼀个⼆分类问题基本不会⽤它。
4. Tanh激活函数几乎适合所有场景。
5. ReLu数是默认函数，如果不确定⽤哪个激活函数，就使⽤ ReLu 或者 Leaky ReLu，再去尝试其他的激活函数。

ReLU激活函数的优点及局限性

• 优点
  （1）从计算角度上，Sigmoid和Tanh都需要计算指数函数，复杂度高，而ReLU只需要一个阈值即可得到激活值。
  （2） ReLU及非饱和性可以有效解决梯度消失的问题，提供相对宽的激活边界。
  （3） ReLU的单侧抑制提供了网络的稀疏表达能力。

• 局限性
  ReLU的局限性在于在其训练过程中会导致神经元死亡的问题。
  由于函数f(x) = max(0, x)导致负梯度在经过该ReLU单元时被置0 ，而且在之后也不被任何数据激活，及流经该神经元的梯度永远为0，不对数据产生响应。在实际训练中，如果学习率设置较大，会导致超过一定比例的神经元不可逆死亡，进而参数无法更新，整个训练过程失败。
  因此，人们设计了ReLU的变种Leaky ReLU:
  
  当x<0时其值不为0，而是一个斜率为a（一般为很小的函数）的线性函数，这样既实现了单侧抑制，又保留了部分负梯度信息以致不完全丢失。

为什么Sigmoid和Tanh会导致梯度消失的问题

• Sigmoid它将输入x映射到区间（0， 1），当x很大时，f(x)趋近于1；当x很小时，f(x)趋近于0。其导数f(x)(1 - f(x))在x很大或很小的时候都趋近于0，造成梯度消失的现象。
• Tanh当x很大时，f(x)趋近于1；当x很小时，f(x)趋近于-1。其导数 1 - (f(z))²，在x很大或很小的时候都趋近于0，同样会出现“梯度消失”。
  实际上，Tanh相当于Sigmoid的平移：tanh(x) = 2sigmoid(2x) - 1.

为什么Tanh收敛速度⽐Sigmoid快？

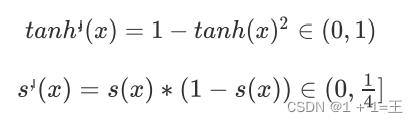
从两者的导数公式可以看到知tanh梯度消失的问题⽐sigmoid轻，所以Tanh收敛速度⽐Sigmoid快。