算法之算法的时间复杂度

Posted 2022-01-28 -YIN

算法之算法的时间复杂度

• • 什么是算法
  • 算法时间复杂度
  • • 程序基本操作执行次数
    • 渐进时间复杂度

时间复杂度是指执行算法所需要的计算工作量，想要了解算法的时间复杂度不妨先看看到底什么是算法。

什么是算法

<1> 算法（Algorithm）：是对特定问题求解方法（步骤）的一种描述，是指令的有限序列，一条指令表示一个或多个操作。

<2>算法的五个特性
  有穷性（Finiteness）
  算法的有穷性是指算法必须能在执行有限个步骤之后结束，且每一步时间都是有穷的。
 确切性(Definiteness)
  算法的每一条指令必须有确切的定义，不存在二义性。
 可行性(Effectiveness)
  算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步骤，即每个计算步骤都可以在有限时间内完成（也称之为有效性）。
 输入(Input)
  一个算法有零个或多个输入，这些输入取于某个特定集合。
 输出(Output)
  一个算法有一个或多个输出，以这些书如同输出有着某些特定关系。

<3>. 算法的设计目标
1 正确性：算法应满足具体问题的需求。
2 可读性：算法应供人阅读交流。可读性好的算法有助于对算法的修改和理解。
3 健壮性：算法应具有容错处理。输入非法数据，能适当做出处理，不产生莫名其妙的输出。
4 高效性（效率与存储量需求）：算法的执行时间高效性与所需存储空间的高效性。
  
< 4>. 算法性能指标：算法的时间复杂度（时间效率）和算法的空间复杂度（空间效率）。

算法时间复杂度

程序基本操作执行次数

//例1
for(int i = 0; i < n; i++)
    printf("运行第%d次\\n", i);
    

如例一这个循环语句，每循环一次执行一次printf()所以设 T(n) 为基本操作次数的函数，n为输入规模。所以该语句 T(n) = 3n。

//例2
int main()

	for(int i = 0; i<n; i++)
	    for(int j = 0; j<i; j++)
	         printf("j = %d \\n", j);
	    
	

而例二T(n) = 1/2(n²) + 1/2(n)。

渐进时间复杂度

定义：对于一个算法，假设其问题的输入大小为n，若存在函数f(n),）就是当n趋于无穷大的时候，T(n)/f(n) 的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。T(n) = O(f(n)),O为算法渐进时间复杂度（asymptotic time complexity），简称时间复杂度。
  
可以理解为：我们通过计算得出一个算法的运行时间 T(n), 与T(n)同数量级的即幂次最高的O(F(n))即为这个算法的时间复杂度。例如：某算法的运行时间T(n) = n+10与n是同阶的（同数量级的），所以称T(n)=O(n)为该算法的时间复杂度。
算法的渐进分析就是要估计：n逐步增大时资源开销T(n)的增长趋势。

算法的时间复杂度是一个函数，它定性描述该算法的运行时间。
一般有以下几种数量级的函数：
O(1) 常数级，O(logn)对数级，O(n)线性级，O(n^c)多项式级，O(Cⁿ)指数级，O(n!)阶乘级

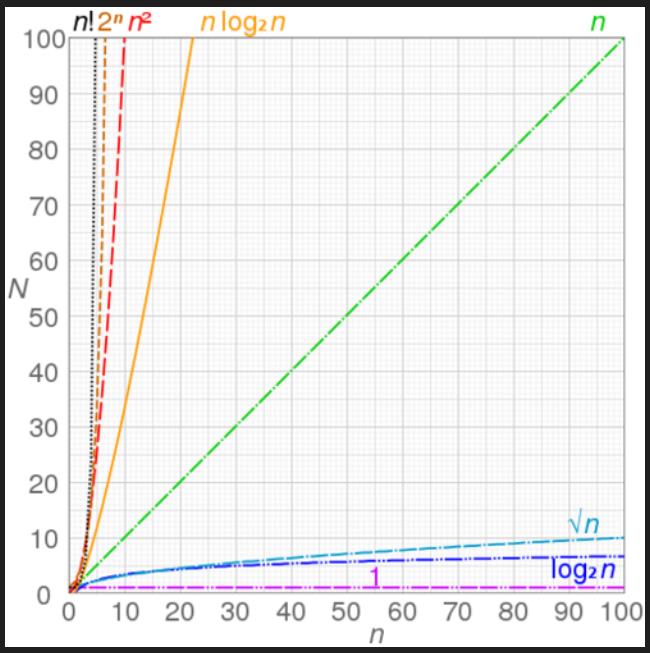
如何推导出时间复杂度呢?有如下几个原则。

●如果运行时间是常数量级，则用常数1表示。
●只保留时间函数中的最高阶项。
●如果最高阶项存在，则省去最高阶项前面的系数。

直白地讲，时间复杂度就是把程序的相对执行时间函数T(n)简化为一个量级，这个数量级可以是1，n， n²， n³…

 对于较复杂的算法,可将它分隔成容易估算的几个部分，然后再利用“O”的求和原则得
到整个算法的时间复杂度。例如，若算法的两个部分的时间复杂度分别为T1(n)=O(f(n))
和T2(n)=O(g(n)),则总的时间复杂度为: T(n) = T1(n)+ T2(n) = O(max(f(n),g(n)))