单应矩阵(Homography)基本概念和代码测试
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了单应矩阵(Homography)基本概念和代码测试相关的知识,希望对你有一定的参考价值。

简 介: 应用棋盘格图片或者相机图片中与标准棋盘格之间的单应矩阵。其中应用到opencv中的findChessboardCorners, findHomographys等函数。 这位利用单应矩阵进行下步的矫正工作提供实验基础。
关键词: 单应矩阵,Homogrpaphy
§00 背景说明
这是在 OpenCV网站 中给出的技术文章,讲述单应矩阵(Homography)的基本概念,并通过测试程序进行介绍。
0.1 介绍
下面的辅导材料利用一些编程代码展示了单应变换(Homograpy)的一些基本概念。关于该理论的详细解释请参见机器视觉课程,或者计算机视觉参考书,比如:
- Multiple View in Computer Vision .
- An tinviation to 3D vision: From images to Geometric Models
- Computer Vision: Algorithms and Applications .
本文中的一些代码可以以下链接找到:
实验中所使用的图片可以在 这个图片链接 下载,但在国内点击无法访问该网站。
§01 基本理论
1.1 什么是单应矩阵?
简单的讲,平面中的单应矩阵涉及到两个平面中的变换(相差一个比例因子)。

其中3×3矩阵
H
H
H就是单应矩阵,由于在估计过程中可以相差一个比例因子,所以单应矩阵具有8个自由变量,通常情况下将该矩阵进行归一化,使得
h
33
=
1
h_33 = 1
h33=1,或者
h
11
2
+
h
12
2
+
h
13
2
+
h
21
2
+
h
22
2
+
h
23
2
+
h
31
2
+
h
32
2
+
h
33
2
=
1
h_11^2 + h_12^2 + h_13^2 + h_21^2 + h_22^2 + h_23^2 + h_31^2 + h_32^2 + h_33^2 = 1
h112+h122+h132+h212+h222+h232+h312+h322+h332=1
下面的例子显示了不同的变换,但最终可以归纳到两个平面之间的转换矩阵。
- 从平面到像平面(图片从像平面获取)

▲ 图1.1.1 从平面转换到像平面
- 两个相机对同一平面取像
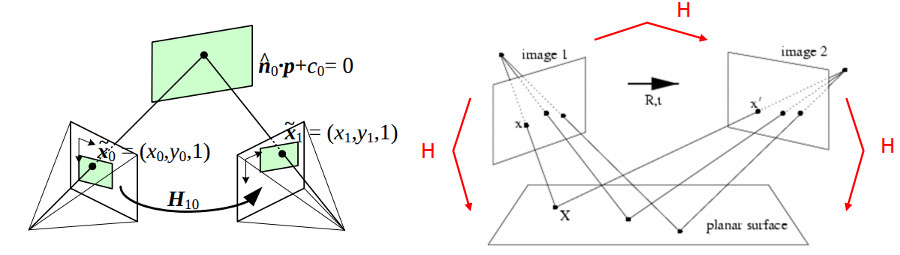
▲ 图1.1.2 两个相机对同一平面取像
- 围绕投影轴旋转相机:
等效考虑一个位于无穷远处的平面上的点。

▲ 图1.1.3 旋转的相机
1.2 如何获得单应矩阵?
如果相应计算两个图片之间的单应矩阵,只有需要确定两个图片中四个以上的对应点的位置。OpenCV通过稳定的算法获得两个图片之间的单应矩阵。可以使用SIFT, 或者SURF算法来寻找两个图片之间对应的像素点。
根据 CV2.findhomography: Things You Should Know 中给出的计算单应矩阵的方法:
假设如下两个点是对应的像素点坐标:
x = ( u v 1 ) , x ′ = ( x y 1 ) x = \\left( \\beginmatrix u\\\\v\\\\1\\\\\\endmatrix \\right),\\,\\,x' = \\left( \\beginmatrix x\\\\y\\\\1\\\\\\endmatrix \\right) x=⎝⎛uv1⎠⎞,x′=⎝⎛xy1⎠⎞
它们之间的单应矩阵为:
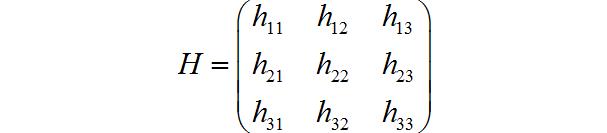
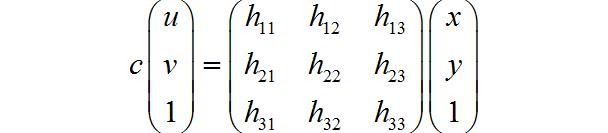
通过消去上述公式中的参数
c
c
c,可以得到如下方程:
A
h
=
0
Ah = 0
Ah=0
其中:
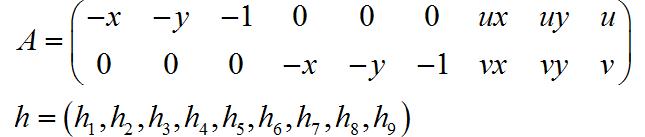
利用cv2中的 findHomography(points1,points2)可以计算两个图片之间的单应矩阵。
1.3 单应矩阵应用场合
-
利用共面点进行相机姿态估计,应用在基于某些标示(Apriltag)下的增强现实。

▲ 图1.2.1 在Apriltag上的增强虚拟现实 -
消除透视效应/视角校正(参见前面第二个例子)

▲ 图1.2.2 透视校正
- 全景图拼接(参见前面第二个、第三个例子)

▲ 图1.2.3 全景图拼接
§02 应用代码
2.1 演示1:从共面点阵进行姿态估计
请注意下面从单应矩阵估计相机姿态是一个应用例子,你需要使用 cv2::solvePnP 来对来自同一平面或者任意物体上的点来估计相机姿态。
单应矩阵可以使用 直接线性变换(DLT)算法来进行估计(见前面理论部分1)。由于对象是在同一平面,所以物体上的点都在同一平面上,在归一化相机成像框架中,描述共面点与像平面上成像位置之间的变换就是单应矩阵。只有当物体是平面,相机内参已知的情况下,相机的姿态才可以从单应矩阵中估计出来。
可以使用棋盘格以及cv2. findChessboardCorners() 得到图片中的角点。
要检测棋盘格角点,首先需要确认棋盘格尺寸(pattenSize),下图是9×6,:
vector<Point2f> corners;
bool found = findChessboardCorners(img, patternSize, corners);

▲ 图2.1.1 棋盘格中的角点
2.1.1 提取棋盘格角点
img = cv2.imread(outfile)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray, (9, 6), None)
if ret:
cv2.drawChessboardCorners(img, (9, 6), corners, ret)
else: print('Error:%s'%ret)
plt.clf()
plt.figure(figsize=(15,15))
plt.axis("off")
plt.imshow(img)
len(corners): 54

▲ 图2.1.2 提取角点 后的图像
2.1.2 计算相机校正参数
obj_p = zeros((9*6, 3), float32)
obj_p[:,:2] = mgrid[0:9, 0:6].T.reshape(-1, 2)
obj_points = []
obj_points.append(obj_p)
img_points = []
img_points.append(corners.reshape(-1, 2))
print(shape(obj_points), shape(img_points))
(1, 54, 以上是关于单应矩阵(Homography)基本概念和代码测试的主要内容,如果未能解决你的问题,请参考以下文章