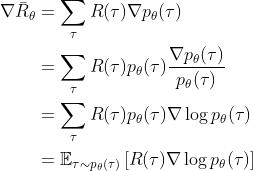RL极简入门:从MDPDP MC TC到Q函数策略学习PPO
Posted v_JULY_v
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了RL极简入门:从MDPDP MC TC到Q函数策略学习PPO相关的知识,希望对你有一定的参考价值。
前言
22年底/23年初ChatGPT大火,在写ChatGPT通俗笔记的过程中,发现ChatGPT背后技术涉及到了RL/RLHF,于是又深入研究RL,研究RL的过程中又发现里面的数学公式相比ML/DL更多,于此激发我一边深入RL,一边系统重修微积分、概率统计,前者成就了本篇RL极简入门,后者成就了另一篇概率统计极简入门(23修订版)
如上篇ChatGPT笔记所说,本文最早是作为ChatGPT笔记的第一部分的,但RL细节众多,如果想完全在上篇笔记里全部介绍清楚,最后篇幅将长之又长同时还影响完读率,为了避免因为篇幅限制而导致RL很多细节阐述的不够细致,故把RL相关的部分从上文中抽取出来独立成本文继续完善(完善记录见本文文末,预计2月底基本成型)。
另,本文有两个特色
- 定位入门。过去一个多月,我翻遍了十来本RL中文书,以及网上各种RL资料,有的真心不错,其余大部分要么就是堆砌概念/公式,要么对已经入门的不错,但对还没入门的初学者极度不友好,很多背景知识甚至公式说明、符号说明没有交待,让初学者经常看得云里雾里
本文会假定大部分读者此前从来没有接触过RL,会尽可能多举例、多配图、多交待,100个台阶,一步一步拾级而上,不出现任何断层 - 推导细致。本文之前,99%的文章都不会把PPO算法从头推到尾,本文会把PPO从零推到尾,按照“RL-策略梯度-重要性采样(重要性权重)-增加基线(避免奖励总为正)-TRPO(加进KL散度约束)-PPO(解决TRPO计算量大的问题)”的顺序逐步介绍每一步推导
且为彻底照顾初学者,本文会解释/说明清楚每一个公式甚至符号,包括推导过程中不省任何一个必要的中间推导步骤,十步推导绝不略成三步
总之,大部分写书、写教材、写文章的人过了那个从不懂到懂的过程,所以懂的人写给不懂的人看,处处都是用已懂的思维去写,而不是用怎么从不懂到懂的思维 去写,未来三年 奋笔疾书,不断给更多初学者普及AI和RL技术
第一部分 从什么是RL、MDP到DP MC TC
1.1 入门强化学习所需掌握的基本概念
1.1.1 什么是强化学习:感知状态-依据策略执行动作-得到奖励
强化学习里面的概念、公式,相比ML/DL特别多,初学者刚学RL时,很容易被接连不断的概念、公式给绕晕,而且经常忘记概念与公式符号表达的一一对应(包括我自己在1.10日之前对好多满是概念/公式的RL书完全看不下去,如今都看得懂了,故如果读文本之前,你正在被RL各种公式困扰,相信看完这篇chatGPT笔记后就完全不一样了)。
为此,我建议学习RL的第一步就是一定要扎实关于RL的一些最基本的概念、公式(不要在扎实基础的阶段图快或图囵吞枣,不然后面得花更多的时间、更大的代价去弥补),且把概念与公式的一一对应关系牢记于心,这很重要。当然,为最大限度的提高本文的可读性,我会尽可能的多举例、多配图。
另,RL之外,像高数/概率统计里的什么叫
- 导数,如下图所示,导数即为

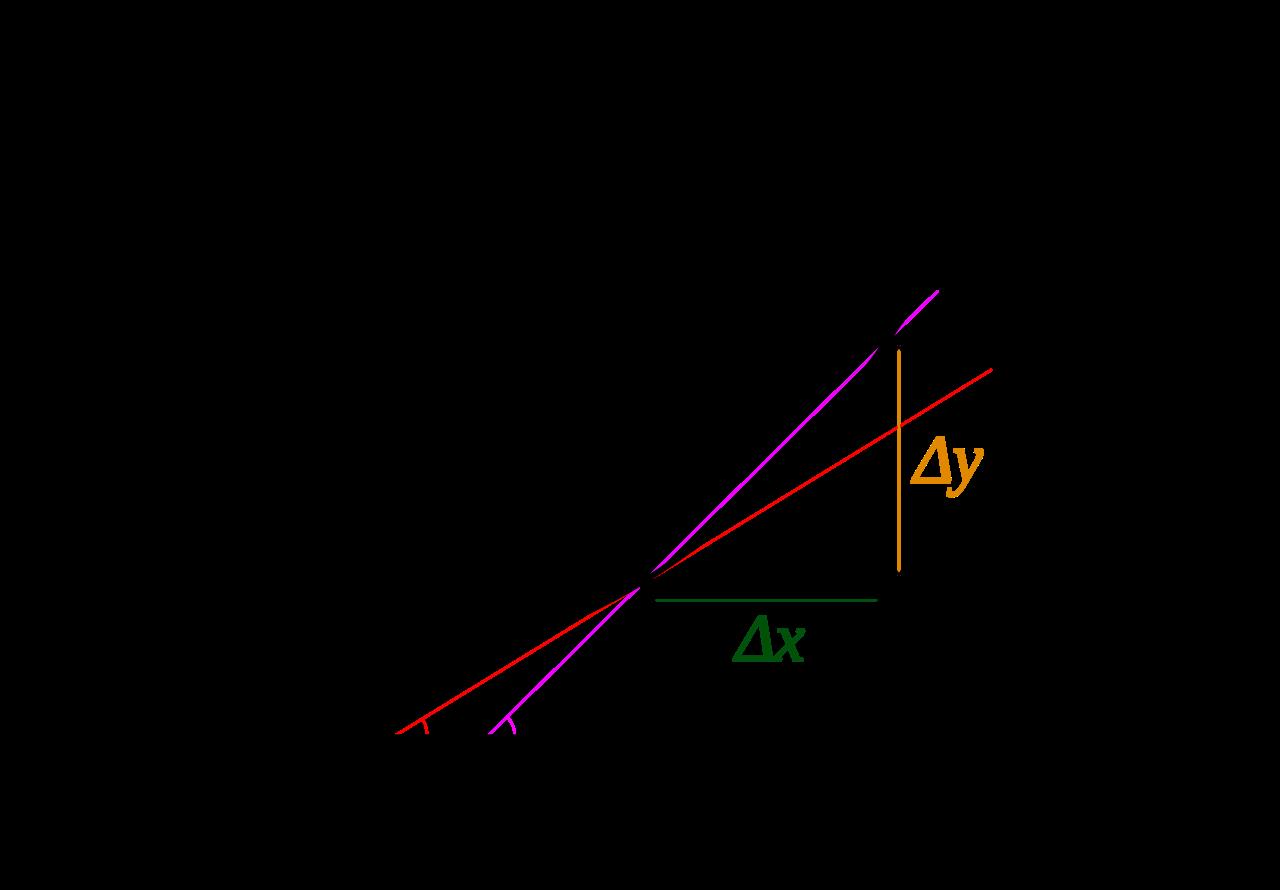
- 期望,如果
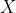 是一个离散的随机变量,输出值为
是一个离散的随机变量,输出值为 ,和输出值相应的概率为
,和输出值相应的概率为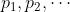 ,且加起来的概率和为1,若级数
,且加起来的概率和为1,若级数 绝对收敛,那么期望值
绝对收敛,那么期望值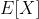 是一个无限数列的和:
是一个无限数列的和:
以及什么叫概率分布、熵/香浓熵(Shannon熵)/交叉熵、相对熵(也称KL散度,即KL divergence)、多元函数、偏导数,以及AI一些最基本的概念比如损失函数、梯度、梯度下降、随机梯度下降(SGD)、学习率等,可以直接Wikipedia上查看相关概念或《概率统计极简入门》等类似笔记,本文则不过多介绍。
毕竟可以为通俗而增加篇幅,但不为了介绍而介绍式的增加篇幅,避免影响完读率,^_^。 话休絮烦,下面进入正题,且先直接给出强化学习的定义和其流程,然后再逐一拆解、说明。
所谓强化学习(Reinforcement Learning,简称RL),是指基于智能体在复杂、不确定的环境中最大化它能获得的奖励,从而达到自主决策的目的。
经典的强化学习模型可以总结为下图的形式(你可以理解为任何强化学习都包含这几个基本部分:智能体、行为、环境、状态、奖励):
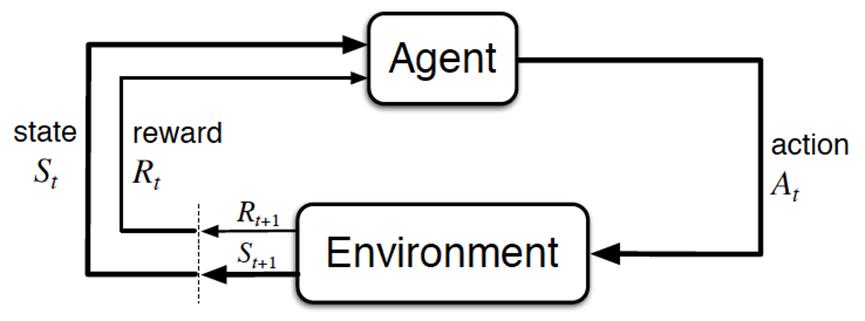
一般的文章在介绍这些概念时很容易一带而过,这里我把每个概念都逐一解释下
- Agent,一般译为智能体,就是我们要训练的模型,类似玩超级玛丽的时候操纵马里奥做出相应的动作,而这个马里奥就是Agent
- action(简记为
 ),玩超级玛丽的时候你会控制马里奥做三个动作,即向左走、向右走和向上跳,而马里奥做的这三个动作就是action
),玩超级玛丽的时候你会控制马里奥做三个动作,即向左走、向右走和向上跳,而马里奥做的这三个动作就是action - Environment,即环境,它是提供reward的某个对象,它可以是AlphaGo中的人类棋手,也可以是自动驾驶中的人类驾驶员,甚至可以是某些游戏AI里的游戏规则
- reward(简记为
 ),这个奖赏可以类比为在明确目标的情况下,接近目标意味着做得好则奖,远离目标意味着做的不好则惩,最终达到收益/奖励最大化,且这个奖励是强化学习的核心
),这个奖赏可以类比为在明确目标的情况下,接近目标意味着做得好则奖,远离目标意味着做的不好则惩,最终达到收益/奖励最大化,且这个奖励是强化学习的核心 - State(简介为
 ),可以理解成环境的状态,简称状态
),可以理解成环境的状态,简称状态
总的而言,Agent通过感知环境Environment从而获取环境的状态state,进而依据策略决策从而执行动作action,最后得到奖励reward(以便下次再到相同状态时能采取更优的动作),然后再继续按此流程“感知状态-依据策略执行动作-得到奖励”循环进行。
可能你还有点懵懵懂懂,没关系,毕竟还有不少背景知识还没有交待,比如RL其实是一个马尔可夫决策过程(Markov decision process,MDP),而为说清楚MDP,得先从随机过程、马尔可夫过程(Markov process,简称MP)开始讲起,故为考虑逻辑清晰,我们还是把整个继承/脉络梳理下。
1.1.2 MDP的前置知识:随机过程、马尔可夫过程、马尔可夫奖励
如HMM学习最佳范例中所说,有一类现象是确定性的现象,比如红绿灯系统,红灯之后一定是红黄、接着绿灯、黄灯,最后又红灯,每一个状态之间的变化是确定的
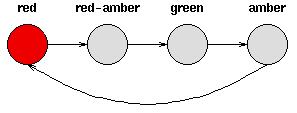
但还有一类现象则不是确定的,比如今天是晴天,谁也没法百分百确定明天一定是晴天还是雨天、阴天
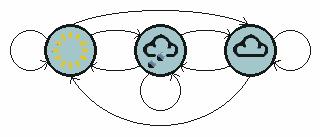
对于这种假设具有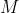 个状态的模型
个状态的模型
- 共有
 个状态转移,因为任何一个状态都有可能是所有状态的下一个转移状态
个状态转移,因为任何一个状态都有可能是所有状态的下一个转移状态 - 每一个状态转移都有一个概率值,称为状态转移概率,相当于从一个状态转移到另一个状态的概率
- 所有的
 个概率可以用一个状态转移矩阵表示
个概率可以用一个状态转移矩阵表示
下面的状态转移矩阵显示的是天气例子中可能的状态转移概率:

也就是说,如果昨天是晴天,那么今天是晴天的概率为0.5,是多云的概率为0.375、是雨天的概率为0.125,且这三种天气状态的概率之和必为1。
接下来,我们参考《动手学强化学习》一书抽象建模下。正如概率论的研究对象是静态的随机现象,而随机过程的研究对象是随时间演变的随机现象(比如天气随时间的变化):
- 随机现象在某时刻t的取值是一个向量随机变量,用
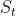 表示
表示
比如上述天气转移矩阵便如下图所示

- 在某时刻t的状态
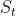 通常取决于t时刻之前的状态,我们将已知历史信息
通常取决于t时刻之前的状态,我们将已知历史信息 时下一个时刻的状态
时下一个时刻的状态 的概率表示成
的概率表示成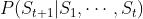
如此,便可以定义一个所有状态对之间的转移概率矩阵

- 当且仅当某时刻的状态只取决于上一时刻的状态时,一个随机过程被称为具有马尔可夫性质,即
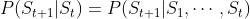 ,当然了,虽说当前状态只看上一个状态,但上一个状态其实包含了更上一个状态的信息,所以不能说当下与历史是无关的
,当然了,虽说当前状态只看上一个状态,但上一个状态其实包含了更上一个状态的信息,所以不能说当下与历史是无关的 - 而具有马尔可夫性质的随机过程便是马尔可夫过程
在马尔可夫过程的基础上加入奖励函数 和折扣因子
和折扣因子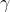 ,就可以得到马尔可夫奖励过程(Markov reward process,MRP)。其中
,就可以得到马尔可夫奖励过程(Markov reward process,MRP)。其中
- 奖励函数,某个状态
 的奖励
的奖励 ,是指转移到该状态
,是指转移到该状态 时可以获得奖励的期望,有
时可以获得奖励的期望,有
PS,有的书上奖励函数和下面回报公式中的的下标
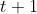 写为
写为 ,其实严格来说,先有
,其实严格来说,先有 时刻的状态/动作之后才有
时刻的状态/动作之后才有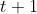 时刻的奖励,但应用中两种下标法又都存在,读者注意辨别
时刻的奖励,但应用中两种下标法又都存在,读者注意辨别 - 此外,实际中,因为一个状态可以得到的奖励是持久的,所有奖励的衰减之和称为回报,可用
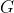 表示未来所有奖励的加权和(考虑到一般越往后某个状态给的回报率越低,也即奖励因子或折扣因子越小,用
表示未来所有奖励的加权和(考虑到一般越往后某个状态给的回报率越低,也即奖励因子或折扣因子越小,用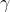 表示),从而有
表示),从而有 
举个例子,一个少年在面对“上大学、去打工、在家啃老”这三种状态,哪一种更能实现人生的价值呢?
相信很多人为长远发展都会选择上大学,因为身边有太多人因为上了大学,而好事连连,比如读研读博留学深造、进入大厂、娶个漂亮老婆、生个聪明孩子
当然了,上大学好处肯定多多,但上大学这个状态对上面4件好事所给予的贡献必然是逐级降低,毕竟越往后,越会有更多或更重要的因素成就更后面的好事,总不能所有好事都百分百归功于最开头选择了“上大学”这个状态/决策嘛
而一个状态的期望回报就称之为这个状态的价值,所有状态的价值则组成了所谓的价值函数,用公式表达为 ,展开一下可得
,展开一下可得

在上式最后一个等式中,前半部分 ,后半部分
,后半部分 可以根据从状态
可以根据从状态 出发的转移概率得到『至于上述推导的最后一步,即为何
出发的转移概率得到『至于上述推导的最后一步,即为何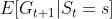 等于
等于 ,待补充』
,待补充』
从而,前后两个部分综合可得
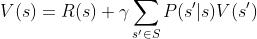
而这就是所谓的贝尔曼方程(bellman equation)。其表达的含义如果简言之的话,则是评估某状态的价值就在于该状态所最终带来的期望回报,具体而言,则是当前状态的奖励,加上该状态所引起的且在折扣因子的作用下后续不同概率所对应各种状态的期望回报。
理论是比较拗口的,为形象起见,举个最简单的“吃饭-抽烟/剔牙”例子
比如你吃完饭后你自己的心情愉悦值即奖励+5,然后下一个状态,有
- 0.6的概率是抽烟(抽烟带来的心情愉悦值即奖励+7,要不说 饭后一支烟 赛过活神仙呢)
- 0.4的概率是剔牙(剔牙带来的奖励值+3)
假设折扣因子
(上文说过了,就是一个状态对后续状态的贡献程度)为0.5,且假定
- 吃饭的状态定义为
,则
- 抽烟的状态定义为
,则
,且由于抽烟之后无后续状态,所以
也是7
- 剔牙的状态定义为
,则
,且由于剔牙之后无后续状态,所以
也是3
从而有:
当从
时,
当从时,
由于状态
和状态
没有后续状态,所以
和
对应的状态值函数分别为
再根据贝尔曼方程
,可得状态
的状态价值函数为
当然,你也可以如此计算(可以很明显的看出,计算量不如上述过程简洁,所以一般优先按上述方式计算)
上述例子的状态比较少所以计算量不大,但当状态一多,则贝尔曼方程的计算量还是比较大的,而求解较大规模的马尔可夫奖励过程中的价值函数时,可以用的方法包括:
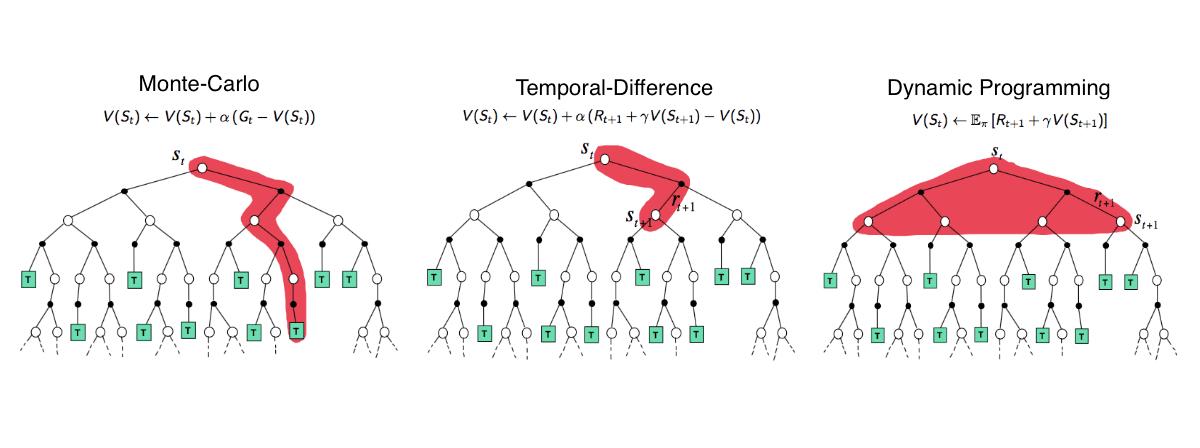
- 动态规划(对的,就是我们数据结构和算法里那个dynamic programming,简称DP),其核心思想在于复杂问题的最优解划分为多个小问题的最优解的求解问题,就像递归一样,且子问题的最优解会被储存起来重复利用
此外,DP和下面两种方法的不同在于,DP需要提前知晓环境和奖励等因素 - 蒙特卡洛(monte carlo,简称MC)方法,也称为统计模拟方法,就是通过大量的随机样本来估算或近似真实值,比如近似圆周率的值、近似微积分、近似期望、近似随机梯度
此外,MC算法是等到一个episode结束得到return以后再借此更新
- 时序差分(temporal difference,简称TD)方法,俗称无模型的RL算法,即不需要事先知道环境的奖励函数和状态转移函数(事实上,很多现实环境中 其MDP的状态转移概率无从得知,也就无法直接使用DP),而Sarsa、Q-learning就是基于时序差分的两大经典算法(细致情况在本文第二部分里介绍)
总的来说,TD每过一个time step就利用奖励和值函数
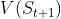 更新一次,当然,这里所说的one-step TD 方法,也可以两步一更新,三步一更新….(不需像MC等到N步以后再更新)
更新一次,当然,这里所说的one-step TD 方法,也可以两步一更新,三步一更新….(不需像MC等到N步以后再更新)
举个例子简单对比下MC与TD,其实就像不同学生做题,有的学生做完全部题才问老师所有题做的对不对 然后下一套试卷更新做题策略,有的学生则做完一题就问老师该题做的对不对 然后下一题即更新做题策略
1.1.3 马尔可夫决策过程(MDP):马尔可夫奖励(MRP) + 智能体动作因素
根据上文我们已经得知,在随机过程的基础上
- 增加马尔可夫性质,即可得马尔可夫过程
- 而再增加奖励,则得到了马尔可夫奖励过程(MRP)
- 如果我们再次增加一个来自外界的刺激比如智能体的动作,就得到了马尔可夫决策过程(MDP)
通俗讲,MRP与MDP的区别就类似随波逐流与水手划船的区别
据强化学习2一书的第47页所说
在马尔可夫决策过程中,
(
是状态的集合)和
(
是奖励的集合)的每个可能的值出现的概率只取决于前一个状态
和前一个动作
(
是动作的集合),并且与更早之前的状态和动作完全无关
下一步的状态 (可能是
(可能是 ),取决于当前的状态
),取决于当前的状态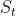 (可能是
(可能是 )以及当前采取的动作
)以及当前采取的动作
 ),它由状态转移概率矩阵和奖励函数两个部分组成
),它由状态转移概率矩阵和奖励函数两个部分组成
- 状态转移概率矩阵

- 奖励函数即

至于过程中采取什么样的动作就涉及到策略policy,策略函数可以表述为 函数(当然,这里的
函数(当然,这里的 跟圆周率没半毛钱关系)
跟圆周率没半毛钱关系)
- 从而可得
 ,意味着输入状态
,意味着输入状态 ,策略函数
,策略函数 输出动作
输出动作
- 此外,还会有这样的表述:
 ,相当于在输入状态
,相当于在输入状态 确定的情况下,输出的动作
确定的情况下,输出的动作 只和参数
只和参数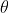 有关,这个
有关,这个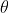 就是策略函数
就是策略函数 的参数
的参数 - 再比如这种
 ,相当于输入一个状态
,相当于输入一个状态 下,智能体采取某个动作
下,智能体采取某个动作 的概率
的概率
通过上文,我们已经知道不同状态出现的概率不一样(比如今天是晴天,那明天是晴天,还是雨天、阴天不一定),同一状态下执行不同动作的概率也不一样(比如即便在天气预报预测明天大概率是天晴的情况下,你大概率不会带伞,但依然不排除你可能会防止突然下雨而带伞)
而有了动作这个因素之后,我们重新梳理下价值函数
- 首先,通过“状态价值函数”对当前状态进行评估
相当于从状态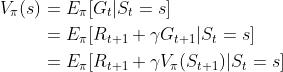
 出发遵循策略
出发遵循策略 能获得的期望回报
能获得的期望回报 - 其次,通过“动作价值函数”对动作的评估
相当于对当前状态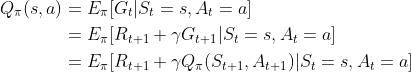
 依据策略
依据策略 执行动作
执行动作 得到的期望回报,这就是大名鼎鼎的
得到的期望回报,这就是大名鼎鼎的 函数,得到
函数,得到 函数后,进入某个状态要采取的最优动作便可以通过
函数后,进入某个状态要采取的最优动作便可以通过 函数得到
函数得到
当有了策略、价值函数和模型3个组成部分后,就形成了一个马尔可夫决策过程(Markov decision process)。如下图所示,这个决策过程可视化了状态之间的转移以及采取的动作。
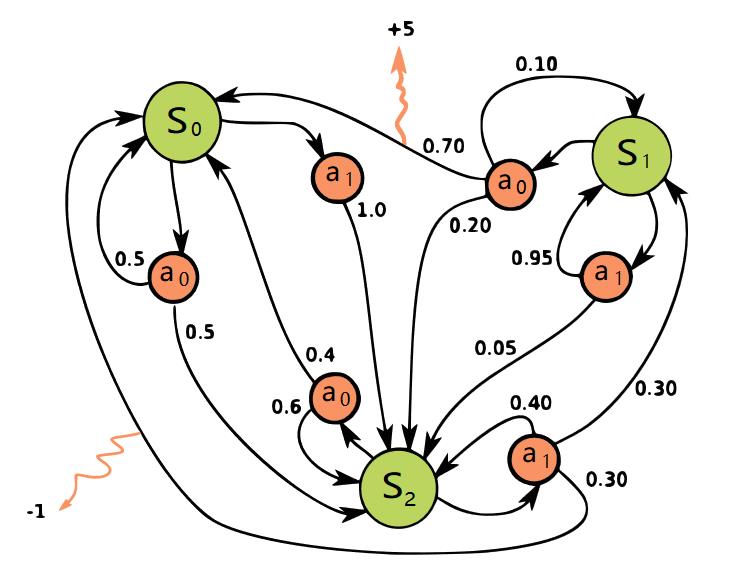
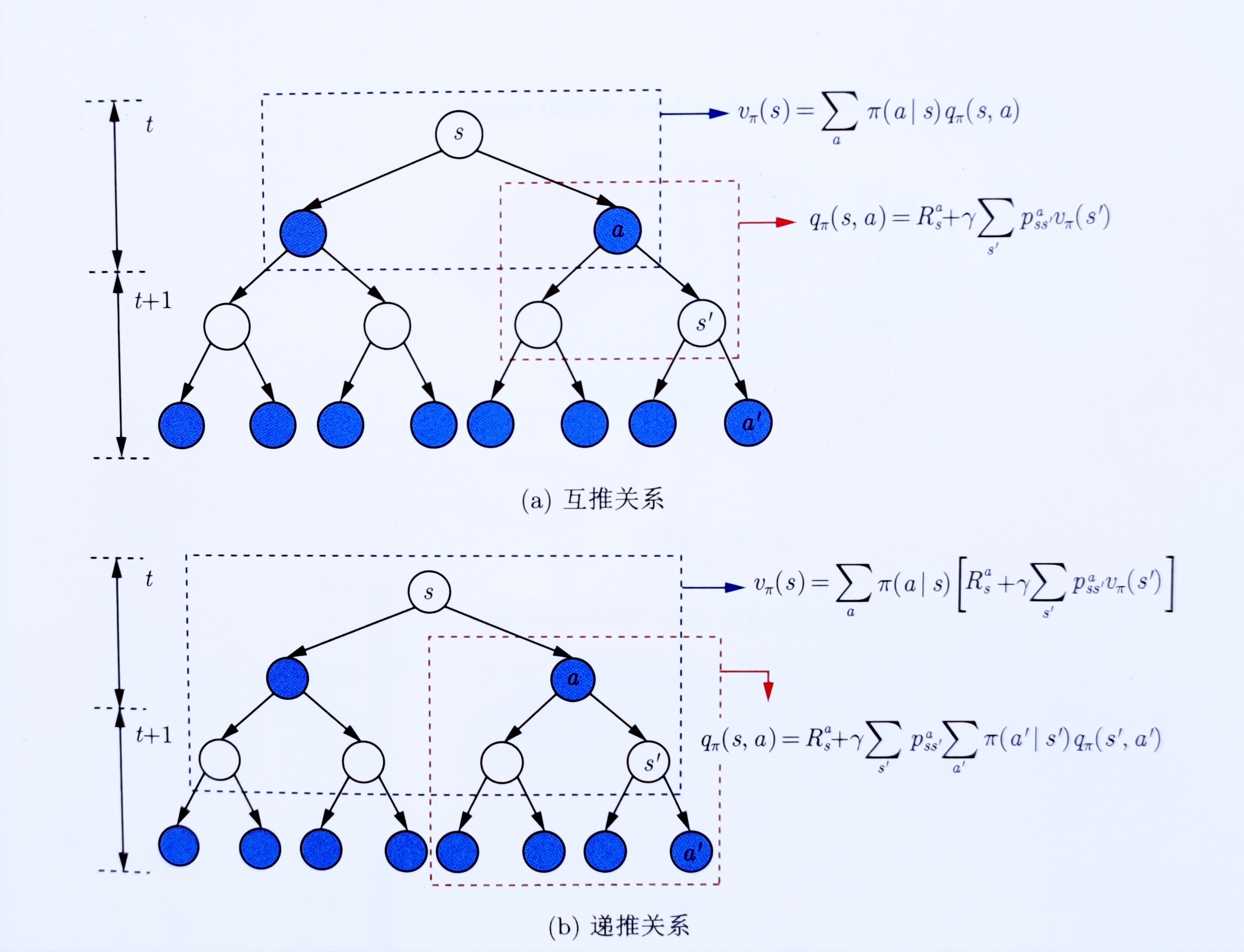
且通过状态转移概率分布,我们可以揭示状态价值函数和动作价值函数之间的联系了
- 在使用策略
 时,状态
时,状态 的价值等于在该状态下基于策略
的价值等于在该状态下基于策略 采取所有动作的概率与相应的价值相乘再求和的结果
采取所有动作的概率与相应的价值相乘再求和的结果 
我猜可能有读者会问怎么来的,简略推导如下『至于如果不清楚从第一个等式到第二个等式怎么来的,待后续详述』
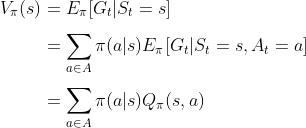
-
而使用策略
 时,在状态
时,在状态 下采取动作
下采取动作 的价值等于当前奖励
的价值等于当前奖励 ,加上经过衰减的所有可能的下一个状态的状态转移概率与相应的价值的乘积
,加上经过衰减的所有可能的下一个状态的状态转移概率与相应的价值的乘积针对这个公式 大部分资料都会一带而过,但不排除会有不少读者问怎么来的,考虑到对于数学公式咱们不能想当然靠直觉的自认为,所以还是得一五一十的推导下
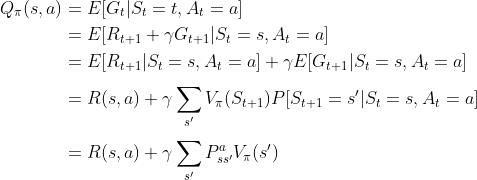
其中,倒数第二步依据的是
 ,最后一步依据的状态转移概率矩阵的定义
,最后一步依据的状态转移概率矩阵的定义
接下来,把上面 和
和
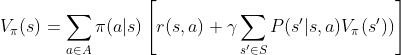
上述过程可用下图形象化表示(配图来自文献51)
计算示例和更多细节待补充..
1.1.4 RL与监督学习的区别和RL方法的分类
此外,RL和监督学习(supervised learning)的区别:
- 监督学习有标签告诉算法什么样的输入对应着什么样的输出(譬如分类、回归等问题)
所以对于监督学习,目标是找到一个最优的模型函数,使其在训练数据集上最小化一个给定的损失函数,相当于最小化预测误差
最优模型 = arg minE (特征,标签)-数据分布 [损失函数(标签,模型(特征)]
RL没有标签告诉它在某种情况下应该做出什么样的行为,只有一个做出一系列行为后最终反馈回来的reward,然后判断当前选择的行为是好是坏
相当于RL的目标是最大化智能体策略在和动态环境交互过程中的价值,而策略的价值可以等价转换成奖励函数在策略的占用度量期望,即最大化累计下来的奖励期望
最优策略 = arg maxE (状态,动作)-策略的占用度量 [奖励函数(状态,动作)]
注,所谓占用度量是为了衡量一个智能体决策与动态环境的交互过程中,采样到一个具体的动作状态对(state-action pair)的概率分布 - 监督学习如果做了比较坏的选择则会立刻反馈给算法
RL的结果反馈有延时,有时候可能需要走了很多步以后才知道之前某步的选择是好还是坏 - 监督学习中输入是独立分布的,即各项数据之间没有关联
RL面对的输入总是在变化,每当算法做出一个行为,它就影响了下一次决策的输入
进一步,RL为得到最优策略从而获取最大化奖励,有
- 基于值函数的方法,通过求解一个状态或者状态下某个动作的估值为手段,从而寻找最佳的价值函数,找到价值函数后,再提取最佳策略
比如Q-learning、DQN等,适合离散的环境下,比如围棋和某些游戏领域 - 基于策略的方法,一般先进行策略评估,即对当前已经搜索到的策略函数进行估值,得到估值后,进行策略改进,不断重复这两步直至策略收敛
比如策略梯度法(policy gradient,简称PG),适合连续动作的场景,比如机器人控制领域
以及Actor-Criti(一般被翻译为演员-评论家算法),Actor学习参数化的策略即策略函数,Criti学习值函数用来评估状态-动作对,不过,Actor-Criti本质上是属于基于策略的算法,毕竟算法的目标是优化一个带参数的策略,只是会额外学习价值函数,从而帮助策略函数更好的学习
此外,还有对策略梯度算法的改进,比如TRPO算法、PPO算法,当然PPO算法也可称之为是一种Actor-Critic架构,本文会重点阐述
第二部分 Q函数
// 待更
第三部分 从策略梯度到重要性采样、TRPO、PPO算法
3.1 策略梯度与其两个问题:采样效率低下与步长难以确定
本节推导的核心内容参考自Easy RL教程等资料(但修正了原教程上部分不太准确的描述,且为让初学者更好懂,补充了大量的解释说明和心得理解,倪老师则帮拆解了部分公式)。
另,都说多一个公式则少一个读者,本文要打破这点,虽然本节推导很多,但每一步推导都有介绍到,不会省略任何一步推导,故不用担心看不懂(对本文任何内容有任何问题,都欢迎随时留言评论)。
3.1.1 什么是策略梯度和梯度计算/更新的流程
策略梯度的核心算法思想是:
- 参数为
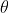 的策略
的策略接受状态
 ,输出动作概率分布,在动作概率分布中采样动作,执行动作(形成运动轨迹
,输出动作概率分布,在动作概率分布中采样动作,执行动作(形成运动轨迹 ),得到奖励
),得到奖励 ,跳到下一个状态
,跳到下一个状态 - 在这样的步骤下,可以使用策略
 收集一批样本,然后使用梯度下降算法学习这些样本,不过当策略
收集一批样本,然后使用梯度下降算法学习这些样本,不过当策略 的参数更新后,这些样本不能继续被使用,还要重新使用策略
的参数更新后,这些样本不能继续被使用,还要重新使用策略 与环境互动收集数据
与环境互动收集数据
比如REINFORCE算法便是常见的策略梯度算法,类似下图所示(下图以及本节大部分配图/公式均来自easy RL教程)

接下来,详细阐述。首先,我们已经知道了策略函数可以如此表示:
其中, 可以理解为一个我们所熟知的神经网络
可以理解为一个我们所熟知的神经网络
- 当你对神经网络有所了解的话,你一定知道通过梯度下降求解损失函数的极小值(忘了的,可以复习下:首先通过正向传播产生拟合值,与标签值做“差”计算,产生误差值,然后对误差值求和产生损失函数,最后对损失函数用梯度下降法求极小值,而优化的对象就是神经网络的参数
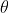 )
) - 类比到
 这个问题上,现在是正向传播产生动作,然后动作在环境中产生奖励值,通过奖励值求和产生评价函数,此时可以针对评价函数做梯度上升(gradient ascent),毕竟能求极小值,便能求极大值,正如误差能最小化,奖励/得分就能最大化
这个问题上,现在是正向传播产生动作,然后动作在环境中产生奖励值,通过奖励值求和产生评价函数,此时可以针对评价函数做梯度上升(gradient ascent),毕竟能求极小值,便能求极大值,正如误差能最小化,奖励/得分就能最大化
如何评价策略的好坏呢?
假设机器人在策略
 表示,从而
表示,从而 表示为一个状态
表示为一个状态 、动作
、动作 、奖励值
、奖励值 不断迁移的过程)
不断迁移的过程)

可能有读者注意到了,既然奖励是延后的,
/
后的奖励怎么用
而非
呢,事实上,sutton RL书上用
表示整条轨迹,其实这样更规范,但考虑到不影响大局和下文的推导,本笔记则暂且不细究了
给定智能体或演员的策略参数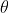 ,可以计算某一条轨迹
,可以计算某一条轨迹 发生的概率为『轨迹
发生的概率为『轨迹 来源于在特定的环境状态下采取特定动作的序列,而特定的状态、特定的动作又分别采样自智能体的动作概率分布
来源于在特定的环境状态下采取特定动作的序列,而特定的状态、特定的动作又分别采样自智能体的动作概率分布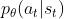 、状态的转换概率分布
、状态的转换概率分布 』
』
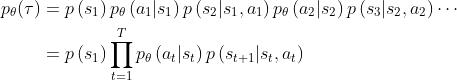
其中,有的资料也会把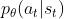 写成为
写成为 ,但由于毕竟是概率,所以更多资料还是写为
,但由于毕竟是概率,所以更多资料还是写为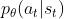
那该策略的评价函数便可以设为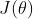 (以
(以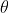 为参数的策略
为参数的策略
 )
)

多说一句,这个策略评价函数为方便理解也可以称之为策略价值函数,就像上文的状态价值函数、动作价值函数,说白了,评估策略(包括状态、动作)的价值,就是看其因此得到的期望奖励。故从某种意义上讲,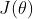 就是
就是
由于每一个轨迹  都有其对应的发生概率,对所有
都有其对应的发生概率,对所有 及其出现的概率进行加权并求和出期望值,可得:
及其出现的概率进行加权并求和出期望值,可得:

上述整个过程如下图所示

通过上文已经知道,想让奖励越大越好,可以使用梯度上升来最大化期望奖励。而要进行梯度上升,先要计算期望奖励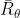 的梯度。
的梯度。
考虑对 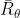 做梯度运算(再次提醒,忘了什么是梯度的,可以通过梯度的Wikipedia,或这个页面:直观形象地理解方向导数与梯度复习下)
做梯度运算(再次提醒,忘了什么是梯度的,可以通过梯度的Wikipedia,或这个页面:直观形象地理解方向导数与梯度复习下)
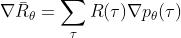
其中,只有 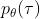 与
与 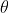 有关。再考虑到
有关。再考虑到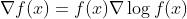 ,可得
,可得

从而进一步转化,可得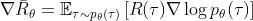 ,表示期望的梯度等于对数概率梯度的期望乘以原始函数。
,表示期望的梯度等于对数概率梯度的期望乘以原始函数。
Em,怎么来的?别急,具体推导是
上述推导 总共4个等式3个步骤,其中,第一步 先分母分子都乘以一个
,第二步 把
代入计算,第三步 根据期望的定义
做个简单转换,此处的
就是

然不巧的是,期望值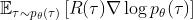 无法计算,按照蒙特卡洛方法的原则,可以用采样的方式采样
无法计算,按照蒙特卡洛方法的原则,可以用采样的方式采样 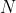 个轨迹
个轨迹 并计算每一个的值,再把每一个的值加起来,如此得到梯度,即(
并计算每一个的值,再把每一个的值加起来,如此得到梯度,即( 上标
上标 代表第
代表第 条轨迹,而
条轨迹,而

 条轨迹里时刻
条轨迹里时刻 的动作、状态)
的动作、状态)