数字信号处理实验集合
Posted Wang_rush
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字信号处理实验集合相关的知识,希望对你有一定的参考价值。
实验一 信号、系统及系统响应
一、实验目的
1、 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解。
2、 熟悉时域离散系统的时域特性。
3、 利用卷积方法观察分析系统的时域特性。
4、 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。
二、实验代码
%dsp11
clear all;
close all;
figure(1)
a1 = FF(444.128,222,222,1000);
n = 0:49;
[b1,K,D] = dtft(a1,n,50);
subplot(3,2,1);%3行2列 1 位置
stem([0:49],a1,'.')%[]:n的范围 a1:纵坐标 画 离散图
xlabel('n')
ylabel('xa(n)');
title('fs=1000');
subplot(3,2,2)
plot(K*D,abs(b1))%: 连续图
xlabel('w')
ylabel('|X(jw)|');
title('fs=1000');
a2 = FF(444.128,222,222,300);
n = 0:49;
[b2,K,D] = dtft(a2,n,50);
subplot(3,2,3);%3行2列 1 位置
stem([0:49],a1,'.')%[]:n的范围 a1:纵坐标 画 离散图
xlabel('n')
ylabel('xa(n)');
title('fs=300');
subplot(3,2,4)
plot(K*D,abs(b2))%: 连续图
xlabel('w')
ylabel('|X(jw)|');
title('fs=300');
a3 = FF(444.128,222,222,200);
n = 0:49;
[b3,K,D] = dtft(a3,n,50);
subplot(3,2,5);%3行2列 1 位置
stem([0:49],a1,'.')%[]:n的范围 a1:纵坐标 画 离散图
xlabel('n')
ylabel('xa(n)');
title('fs=200');
subplot(3,2,6)
plot(K*D,abs(b3))%: 连续图
xlabel('w')
ylabel('|X(jw)|');
title('fs=200');
%dsp12
clear all;
close all;
figure(2)
[Xb,n1]=impseq(0,0,0);
[Ha,n2]=stepseq(0,0,9);
Hb=impseq(0,0,3)+2.5*impseq(1,0,3)+2.5*impseq(2,0,3)+impseq(3,0,3);
subplot(3,2,1);
stem(n1,Xb,'.');
xlabel('n');
ylabel('xb(n)');
N=64;
[A1,k1,D1]=dtft(Xb,n1,N);
subplot(3,2,2),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Xb(jw)|');
subplot(3,2,3);
stem([0:3],Hb,'.');
xlabel('n');
ylabel('hb(n)');
N=64;
[A1,k1,D1]=dtft(Hb,0:3,N);
subplot(3,2,4),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Hb(jw)|');
Xb=double(Xb);
Hb=double(Hb);
y=conv(Hb,Xb);
subplot(3,2,5);
stem([0:3],y,'.');
xlabel('w');
ylabel('yb(n)');
N=64;
[A1,k1,D1]=dtft(y,0:3,N);
subplot(3,2,6),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Y1(jw)|');
figure(3)
Ha=double(Ha);
y=conv(Ha,Ha);
subplot(2,2,1);
stem(n2,Ha,'.');
xlabel('n');
ylabel('Ha(n)');
N=64;
[A1,k1,D1]=dtft(Ha,n2,N);
subplot(2,2,2),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Ha(jw)|');
subplot(2,2,3);
stem([0:18],y,'.');
xlabel('n');
ylabel('y(n)');
N=64;
[A1,k1,D1]=dtft(y,0:18,N);
subplot(2,2,4),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Y2(jw)|');
figure(4)
[c,n4]=stepseq(0,0,4);
Ha=double(Ha);
y=conv(Ha,c);
subplot(2,2,1);
stem(n4,c,'.');
xlabel('n');
ylabel('Ha(n)');
N=64;
[A1,k1,D1]=dtft(c,n4,N);
subplot(2,2,2),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Xc(jw)|');
subplot(2,2,3);
stem([0:13],y,'.');
xlabel('n');
ylabel('y(n)');
N=64;
[A1,k1,D1]=dtft(y,0:13,N);
subplot(2,2,4),plot(k1*D1),abs(A1);
xlabel('w');
ylabel('|Y(jw)|');
%dsp13
clear all;
close all;
figure(5)
Xa = FF(4, 0.4, 2.073, 1);
Xb = impseq(0, 0, 1);
Hb = impseq(0, 0, 3) + 2.5 * impseq(1, 0, 3) + 2.5 * impseq(2, 0, 3) + impseq(3, 0, 3);
b1 = abs(fft(Xa));
subplot(3, 2, 1);
stem([0:49], Xa, '.');
xlabel('n');
ylabel('xa(n)');
title('fs = 1');
N = 512;
[A1, k1, D1] = dft2(Xa, N);
subplot(3, 2, 2), plot(k1 * D1, abs(A1));
xlabel('w');
ylabel('|Xa(jw)|');
subplot(3, 2, 3);
stem([0:3], Hb, '.');
xlabel('n');
ylabel('Hb(n)');
N = 512;
[B1, k1, D1] = dft2(Hb, N);
subplot(3, 2, 4), plot(k1 * D1, abs(B1));
xlabel('w');
ylabel('|Hb(jw)|');
Hb = double(Hb);
Xa = double(Xa);
y = conv(Hb, Xa);
%Y = abs(fft(y, 64));
subplot(3, 2, 5);
stem([0:52], y, '.');
xlabel('n');
ylabel('y(n)');
N = 512;
[Y1, k1, D1] = dft2(y, N);
subplot(3, 2, 6), plot(k1 * D1, abs(Y1));
xlabel('w');
ylabel('|Y(jw)|');
figure(6)
XH = A1 .* B1;
yi = ifft(XH, 512);
subplot(2, 1, 1);
stem([0:52], y, '.');
xlabel('n');
ylabel('y(n)');
subplot(2, 1, 2);
stem([0:52], real(yi(1:53)), '.');
xlabel('n');
ylabel('yi(n)');
%impseq
function [x, n] = impseq(n0, n1, n2)
n = [n1:n2];
x = [(n - n0) == 0];
%stepseq
function [x,n] = stepseq(n0,n1,n2)
n = [n1:n2];
x = [(n-n0) >= 0];
%FF
function c = FF(A,a,w,fs)
n = 0: 49;
c = A*exp((-a)*n/fs).*sin(w*n/fs).*stepseq(0,0,49);
%dtft
function [X,K,D] = dtft(x,n,N)%K:离散频谱的点的序号 D :离散频谱点的间隔 X:离散频谱
K = floor((-N/2+0.5):(N/2-0.5));
D = 2*pi/N;
X= x*exp(-j*D*n'*K);%n’转之
实验运行结果截图
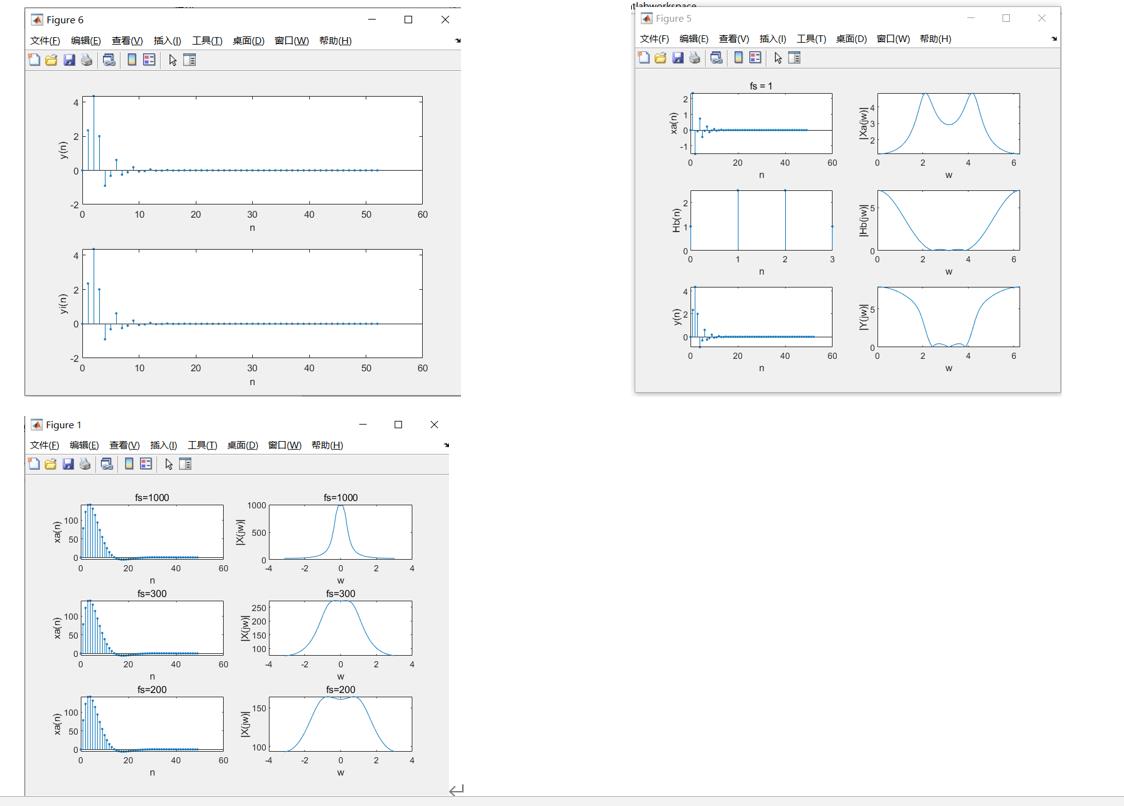
实验二 用FFT作谱分析
一、实验目的
1、 进一步加深DFT算法原理和基本性质的理解(因为FFT只是DFT的一种快速算法,所以FFT的运算结果必然满足DFT的基本性质)。
2、 熟悉FFT算法原理和FFT子程序的应用。
3、 学习用FFT对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
二、实验代码
%dsp2
clear all;
close all;
x1=[1,1,1,1];
x2=[1,2,3,4,4,3,2,1];
x3=[4,3,2,1,1,2,3,4];
x6=xinhao6(16,32);
N1=8;
n=0:N1-1;
x4=cos(以上是关于数字信号处理实验集合的主要内容,如果未能解决你的问题,请参考以下文章