线性代数：矩阵的逆

Posted 2023-02-25 herr_edoc

关于矩阵的逆有很多性质和定理，例如，可逆矩阵一定是方阵、满秩矩阵、非奇异矩阵，可逆矩阵的行列式的值不为零等等。在证明一个矩阵是不可逆矩阵时，Strang教授讲了一种几何的思路：

矩阵不可逆的证明

根据可逆矩阵的定义，如果方阵$\mathbf{A}\ast \mathbf{B}=\mathbf{I}$，则$\mathbf{A}$和$\mathbf{B}$互称逆矩阵。下面是一个二维不可逆矩阵的例子，有矩阵$\mathbf{A}=\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]$，如果$\mathbf{A}$可逆，则有$\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]\ast \mathbf{B}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$，对矩阵$\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]$中的两个列向量作某种线性组合会得到列向量$\left[\begin{array}{c}1\\ 0\end{array}\right]$。从图上可以很明显看出来，不管是什么线性组合都无法得到列向量$\left[\begin{array}{c}1\\ 0\end{array}\right]$，所以，矩阵$\mathbf{A}$不是可逆矩阵。

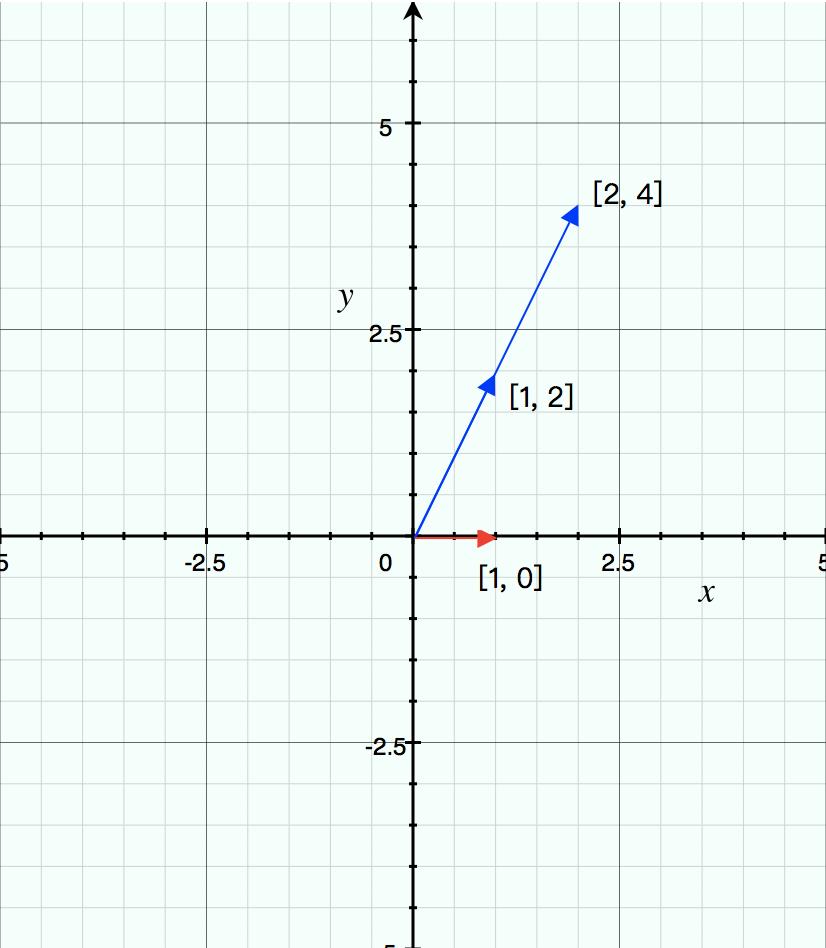
Strang教授把大部分抽象的矩阵运算用几何的思维呈现，非常有利于理解矩阵。

求逆

我们可以用高斯消元法（Gauss Elimination）求解方程组的解，在求矩阵的逆时则可以用高斯-若尔当消元法（Gauss-Jordan Elimination）。
方程组可以用$\mathbf{A}\ast \mathbf{x}=\mathbf{b}$来表示，通过对增广矩阵$\left[\begin{array}{c}\mathbf{A}\text{|}\mathbf{b}\end{array}\right]$进行初等变换，然后再用“回代”法即可求得方程组的解。在求矩阵的逆时（$\mathbf{A}\ast \mathbf{B}=\mathbf{I}$），可以把矩阵$\mathbf{B}$看成多个列向量（$\mathbf{x}$）的组合，那么求解矩阵$\mathbf{A}$的逆就可以看成是同时求解多个方程组，即通过初等变换将增广矩阵$\left[\begin{array}{c}\mathbf{A}\text{|}\mathbf{I}\end{array}\right]$变换成$\left[\begin{array}{c}\mathbf{I}\text{|}\mathbf{B}\end{array}\right]$，得到的矩阵$\mathbf{B}$即为$\mathbf{A}$的逆矩阵。