golang Go：Newton的平方根方法

Posted 2021-05-24

/*
A Tour of Go: page 44
http://tour.golang.org/#44

Exercise: Loops and Functions

As a simple way to play with functions and loops, implement the square root function using Newton's method.

In this case, Newton's method is to approximate Sqrt(x) by picking a starting point z and then repeating: z - (z*z - x) / (2 * z)


To begin with, just repeat that calculation 10 times and see how close you get to the answer for various values (1, 2, 3, ...).

Next, change the loop condition to stop once the value has stopped changing (or only changes by a very small delta). See if that's more or fewer iterations. How close are you to the math.Sqrt?

Hint: to declare and initialize a floating point value, give it floating point syntax or use a conversion:

	z := float64(1)
	z := 1.0
*/

package main

import (
	"fmt"
	"math"
)

const DELTA = 0.0000001
const INITIAL_Z = 100.0

func Sqrt(x float64) (z float64) {
    z = INITIAL_Z
    
    step := func() float64 {
    	return z - (z*z - x) / (2 * z)
    }
    
    for zz := step(); math.Abs(zz - z) > DELTA
    {
    	z = zz
	zz = step()
    }
    return
}

func main() {
	fmt.Println(Sqrt(500))
	fmt.Println(math.Sqrt(500))
}

使用牛顿-拉弗森法定义平方根函数（Newton-Raphson method Square Root Python）

牛顿法（Newton’s method）又称为牛顿-拉弗森法（Newton-Raphson method），是一种近似求解实数方程式的方法。（注：Joseph Raphson在1690年出版的《一般方程分析》中提出了后来被称为“牛顿-拉弗森法”的数学方法，牛顿于1671年写成的著作《流数法》中亦包括了这个方法，但该书在1736年才出版。）

 

之前的一篇博客中提到的二分法可以求解方根，而使用牛顿迭代法可以更快地解出方根。现在，人们使用的计算器里面大多数都是运用的牛顿迭代法。

 

 

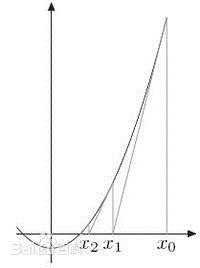
假设n=x²，现在需要求n的方根，n=x²亦即x²-n=0，把它转换成方程式f(x)=x²-n，如上图所示。

选取作为求解方根的初始近似值，过点作切线T，T的方程为，求出T与x轴交点的横坐标，称x₁为n方根的一次近似值。

过点再作切线，并求得该切线与x轴交点的横坐标，称为n方根的二次近似值。

以此类推，得到牛顿法的迭代公式： （注：f‘(x_n)是导数，这里也就是切线的斜率，数值是2*x_n）。

猜测值在经过多次迭代后会越来越接近曲线的根，用数学术语来说就是，这个方程式在的时候收敛，故能求得近似n方根的值。

 

总的图示如下： 

 

 

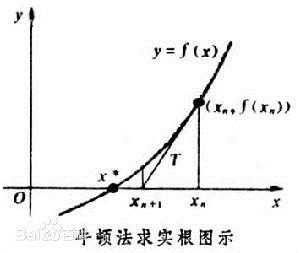
代码如下：

def sqrt_NR(n):
    ‘‘‘为了方便起见，先假设n为正数‘‘‘
    guess=n/2  # 设置初始猜测值为n的一半
    diff=guess**2-n  # f(Xn)
    count=1  # 设置猜测次数起始值为1
    while abs(diff)>0.001 and count<100: # 当猜测值的平方和n本身的差值无限接近误差值时，循环才会停止；同时设置猜测次数不超过100次
        guess=guess-diff/(2*guess)  # 根据牛顿法的迭代公式Xn+1=Xn-f(Xn)/f‘(Xn)，将上一次的猜测值减去f(Xn)/导数的值赋予新的猜测值
        diff=guess**2-n  # 更新f(Xn)
        count+=1  # 猜测次数每次增加1
    return guess

 

调用此函数试一下：

print(sqrt_NR(8))

 

运行结果如下：

2.8284313725490198

 

二分法和牛顿法对比：

把这两个函数的eplison都设置为0.01，增加显示count

运行：

print(“二分法： ", sqrt_bi(8))
print("牛顿法： ", sqrt_NR(8))

 结果如下：

二分法：    (2.828369140625, 15)

牛顿法：    (2.8284313725490198, 4)

 

是不是牛顿法比二分法快多了？

 

参考：麻省理工学院公开课：计算机科学及编程导论  （第6课）