数据结构与算法递归全流程详细剖析 | 详解图的深度优先遍历

Posted 2023-02-23 大数据小禅

🚀 作者 ：“大数据小禅”

🚀文章简介：本篇文章属于数据结构与算法系列文章，这篇文章会对算法中的递归进行一个详细的介绍，不仅是概念，而是从运行过程中的每一步进行详细分析。并使用递归的方式来完成数据结构图的深度优先遍历

🚀个人主页： 大数据小禅

图的遍历与递归

• • • 1. 递归初体验
    • • 1.1 使用递归实现阶乘操作
    • 2. 递归调用详解
    • • 2.1 普通的函数递归调用过程
      • 2.2 递归函数的调用过程
    • 3. 图的深度优先遍历DFS
    • • 3.1 图的表示
      • 3.2 图的深度优先遍历
      • 3.3 详解深度优先种的递归遍历
      • 3.4 递归过程执行流程详解

1. 递归初体验

---

• 什么是递归
  • 递归就是一个程序或者是函数在调用自身的一种方法。
  • 这一种方法通常是把一个复杂的问题经过层层的转化为跟原问题相似但规模较小的问题来求解。
  • 递归策略只需要使用少量的程序就可以把解题过程需要多次的重复计算描述出来，大大的减少了代码量。
  • 一般来说递归需要边界条件，递归前进段和递归返回段，当边界条件不满足的时候，递归前进，当边界条件满足的时候就递归返回。
• 递归必须具备条件
  • 自己调用自己
  • 有终止条件

1.1 使用递归实现阶乘操作

        public static void main(String[] args) 
            int result = factorial(5);
            System.out.println("5的阶乘结果是："+result);

        
        // 求n的阶乘

        public static int factorial(int n) 
            if (n <=1) 
                return 1;
            
            return n * factorial(n - 1);
        
输出：
5的阶乘结果是：120

2. 递归调用详解

2.1 普通的函数递归调用过程

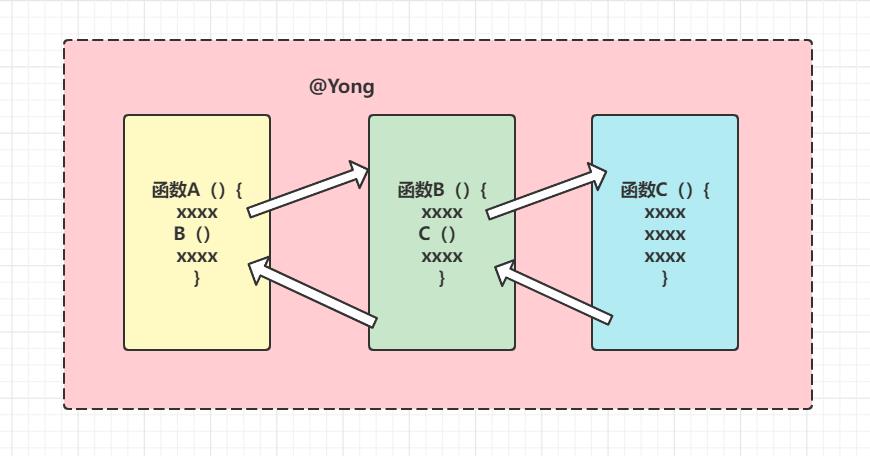
• 步骤1：函数A执行，调用函数B，这个时候A函数暂时挂起，函数B调用函数C，B暂时挂起
• 步骤2：函数C执行完之后，就回到B函数调用C函数的地方，去执行C函数调用后B函数还没执行完的的其他逻辑:。
• 步骤3：整个执行完之后B函数也执行完了，再返回到A函数调用B函数的地方，继续执行B函数下面的所有逻辑
  

2.2 递归函数的调用过程

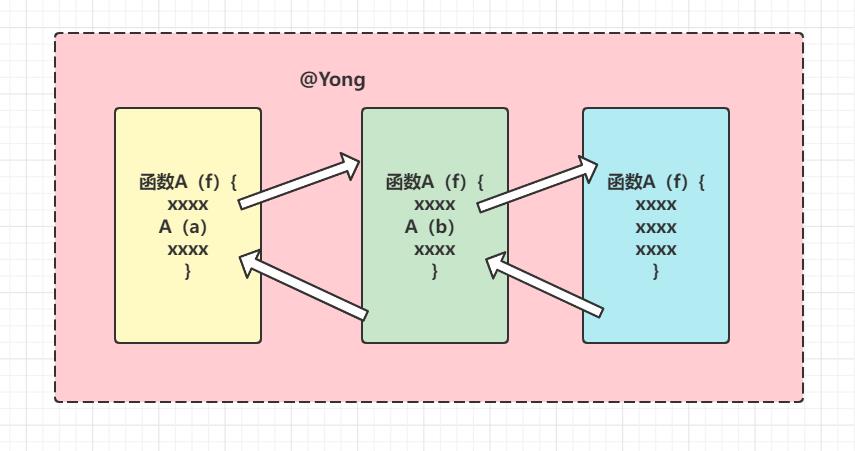
• 跟普通函数的调用没什么区别，就是每一次调用的是自己，调用自己后挂起，去执行调用的本身的函数。
• 传入的参数会变化，执行到了终止的条件之后一样往回执行之前接下去没有执行完的代码。
  

3. 图的深度优先遍历DFS

---

• 图是一种数据结构 每一种数据结构都必须有"遍历"的方式

• 很多算法 本质就是“遍历” ** 对于图论，真正理解"遍历"可以解决80%**的面试问题

• 通常不会用图这种数据结构来存储数据，或者进行搜索查找的任务。更多的是存储一种拓扑关系，之后通过图论算法来寻找这种拓扑关系中隐藏的性质。比如看两个节点是否相连，最短路径，或者一个图的最小生成树

• 对树的遍历一般不需要整棵树的元素遍历 但是图的话一般是寻找图中某种拓扑结构的性质，想要得到一般需要把整个图遍历一遍，遍历过程中可能还需要不断记录一些信息，最终得到结果。

3.1 图的表示

图的基本概念与图的基本表示
图的表示可以看我的前一篇文章 这里采用邻接表的方式来表示一个图无向无权图。

3.2 图的深度优先遍历

1 深度优先遍历，从给定的起始节点出发，起始节点一般有多个相邻节点。深度优先遍历的策略就是先访问起始节点的第一个邻接节点，
然后再以这个被访问的邻接结点作为新的起始节点，再访问它的第一个邻接结点。
指导遍历完成

2 深度优先遍历可通过递归的方式来完成，下面分析实现的核心代码与过程

3.3 详解深度优先种的递归遍历

核心部分代码：

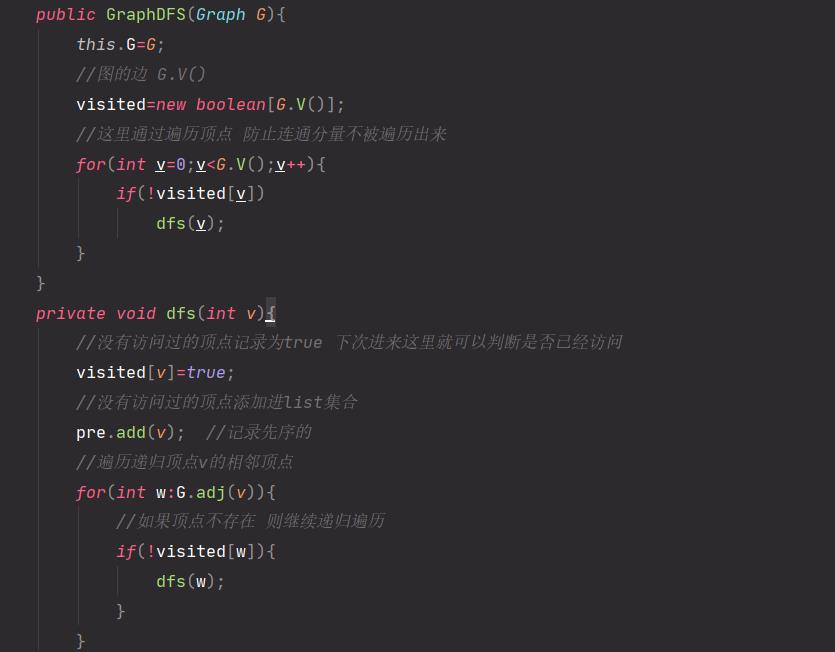
3.4 递归过程执行流程详解

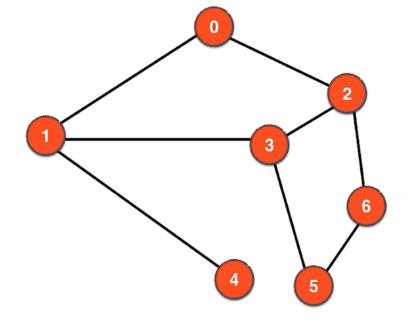
1. int v=0开始，执行dfs(0)，当前数组空，数组下标为0的地方标记为true,0添加进List。
2. 访问0的相邻节点，1跟2，发现1不存在数组中，调用dfs(1)，这个时候dfs(0)挂起先执行dfs(1)
3. 数组下标为1的地方设置为true，把1添加进List,遍历节点1的相邻节点 0,3,4。这个时候0已经在数组中存在，跳过继续看3，发现3不在数组中，则把dfs(1)挂起，调用dfs(3).
4. 把3添加进List中，3下标设置为true，继续走下面的逻辑。依次类推指导调用到dfs(5)。此时的调用路径是dfs(0)->dfs(1)->dfs(3)->dfs(2)->dfs(6)->dfs(5)。
5. 此时的List中遍历结果为 0 1 3 2 6 5。调用到dfs(5)的时候发现5的所有相邻顶点都访问过了。
6. 表示对于dfs(5)的调用for循环已经结束了，下面没有其他逻辑了。这个时候就要返回上一次递归调用的过程dfs(6)了。dfs(0)->dfs(1)->dfs(3)->dfs(2)->dfs(6)
7. 回到dfs(6)，把dfs(6)没执行完的逻辑继续执行。上次对dfs(6)执行到了遇到了5这个节点的时候就进行递归调用了，而5这个顶点已经结束调用，对于6这个顶点也是遍历完了。退回dfs(0)->dfs(1)->dfs(3)->dfs(2)，依次类推，直到退回到dfs(3)这个时候，上次这个函数执行到了遍历递归节点2的时候就去递归调用了，这个时候dfs(2)已经调用完了，现在可以继续往下遍历，还有节点5.
8. 这个时候dfs(5)，5的相关顶点也已经是true了也不需要递归调用了，继续往回退dfs(0)->dfs(1)。
9. 上次调用dfs(1)的时候执行到了顶点3，现在继续往下执行，调用了dfs(4)，这个时候顶点4还是没有被调用过的，记录为true，加入到List。 0 1 3 2 6 5 4。dfs(0)->dfs(1)->dfs(4).
10. 调用完dfs(4),其相邻的顶点也已经被遍历完了，这个时候继续往回退，直到dfs(0)执行完相应顶点逻辑。到这里就遍历完成。

遍历结果

[0, 1, 3, 2, 6, 5, 4]