通俗语言描述人工神经网络，反向传播算法，卷积神经网络

Posted 2023-02-22 TaylorHere

通俗语言描述人工神经网络，反向传播算法，卷积神经网络－－人工神经网络

关键词：Artificial Neural Networks，ANN、Neural Networks ，NN、BackPropagation，BP、Convolutional Neural Network，CNN

什么是人工神经网络

人工神经网络是计算机科学领域的一个研究方向，主要是通过模仿生物神经网络的工作原理来做一些复杂的分类运算，总体来说神经网络只是一种计算方法，它可以并行、容错、可以硬件实现以及自我学习特性，是神经网络的几个基本优点，也是神经网络计算方法与传统方法的区别所在。

神经网络的结构

一个神经网络由很多神经元组成，典型的神经网络和神经元如下图：
人工神经网络：

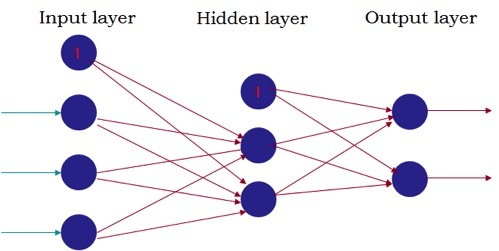
人工神经网络神经元：

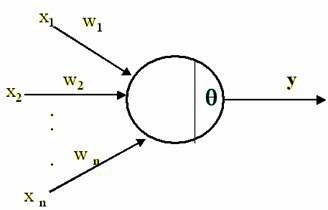
神经元

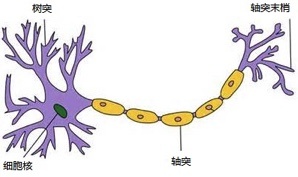
通过上图我们会发现神经网络是人工神经元组成的网络，并且每个人工神经元和真实的神经元极为相似，那么人造神经元是怎么模拟神经元工作的呢？

神经元的工作方式

一个神经元主要由树突＋细胞核＋轴突组成，一个神经元树突用来和其他神经元的轴突末梢相连接，神经元会传递电信号，而不同的链接的电信号传递的时间、强弱等都会有差别。

人造神经元的工作方式

一个人造神经元主要由输入路径＋激活函数＋输出路径组成，一个人造神经元的输入和其他人造神经元的输出相连接，人造神经元传递的是数值，而每条输入路径的长度或者说权重不同以模拟神经元的电信号传递的差别。
在上图中，x1、x2…xn是输入路径y是输出路径
输入经过激活函数后变为输出y传递出去
那么什么是激活函数呢？

什么是激活函数

激活函数是一种非线性函数，常用的激活函数是sigmoid

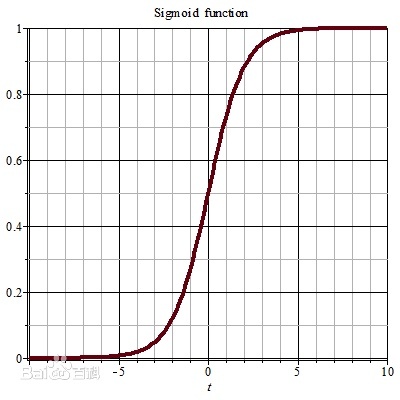
这是一种“S”型（sigmoid）函数,它的值域为(0,1)，曲线的顶部无限逼近1，底部无限逼近0，所以它可以表述输入x可能是某一类型的概率是多少，sigmoid函数的公式定义如下：

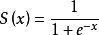
假设s(x)=1的意义是输入x是A类，那么假设输入x＝2.20,那么s(x)≈0.8,的意义就是x为A类的概率为0.8.
也就是说这个函数具有把事物分成两类的能力，而这就是一个被激活的神经元应该做的事：把信号（或叫数据）分类
事实上最简单的直线也能把数据分类，如下：

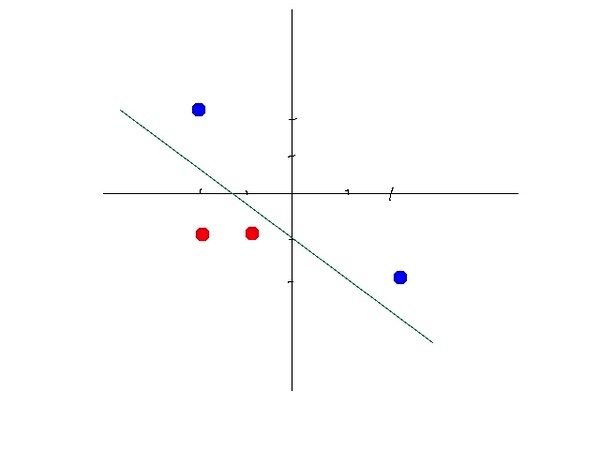
但是直线的分类能力太差，比如以下数据：

一条线可是不能分干净的。
这时就需要一个非线性的函数来做分类，这个函数就是sigmoid函数。
所以总的来说：激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。
事实上激活函数还要tanh、relu函数等，他们都有非线性，容易求导数，光滑等特征。

神经网络的结构

一个标准的神经网络如下：

这个神经网络一共有三层，分别为输入层，隐藏层和输出层。
在输入层里，最左边三条青色的线是输入数据，最上方的那个神经元叫做bias－unit，偏执神经元，数据经过第一层后，经过权重和激活函数的运算转化为第二层的输入（并且神经元变少了），经过隐藏层后，最终输出层产生两个输出（比如可能是：0或1。
一个神经网络一定有一个输入层，和一个输出层，中间可以有不同数量的隐藏层。

神经网络的工作方式

我们用这个数据做为演示：

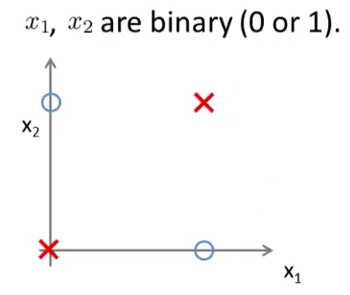
这个数据其实是表达了以下概念：
y＝x1 XNOR x2
即NOT(XOR)
在看怎么解决反异或之前，我们看看怎么解决AND的问题。

AND问题

神经网络图看下：

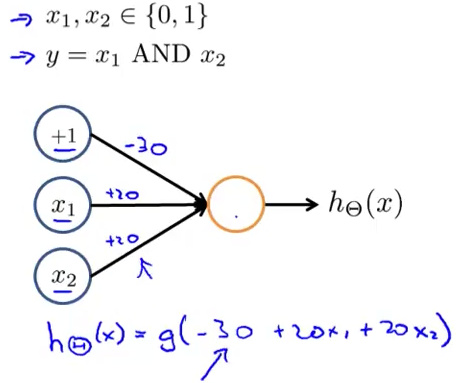
事实上这是只有一个神经元的神经网络，它的输入为x1和x2，外加一个偏执单元。
x1和x2的输入权重都为+20，偏执单元的权重为-30，激活单元按以下公式计算
h(x)=g(20x1+20x2-30)
也就是把输入乘上权重，然后作为激活函数的参数，进行计算
我们来看看这个神经网络的计算结果

为什么g(-30)≈0呢？
我们再看看sigmoid函数：

事实上在x接近－5的时候，函数值以及非常接近0了，所以当函数值远大于－5的时候函数值一定是非常接近0的。
同理我们可以设计一个可以计算OR算法的神经网络：

同样一个结构我们修改了偏执单元和输入单元的权重
接着我们设计一个NOT神经网络：

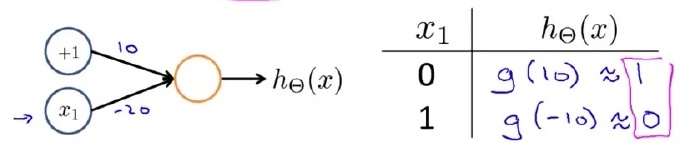
结合以上知识我们可以轻松设计一下三个神经网络：

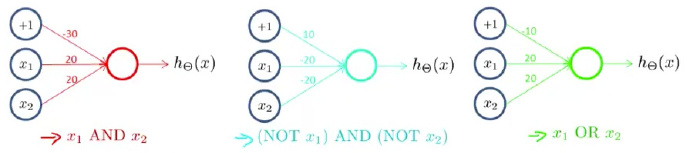
如果我们把这三个神经网络结合起来呢？

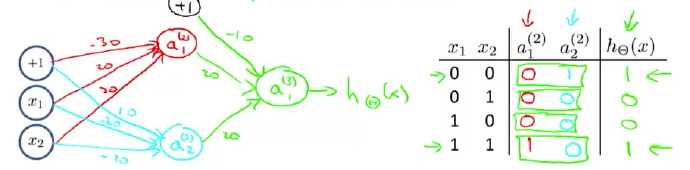
没错，这就是“非异或”神经网络的实现。

正向传播

正向传播，又叫前向传播，上文演示的计算方式就是正向传播。
在我们用公式演算前，先看看怎样用符号表示神经网络：

我们用a来表示一个神经元的上标j表达a所在的层，i表示a在某一层中的序号
我们用大写的theta来表示权重矩阵，上标j表示从j层到j＋1层所有的权重构成的矩阵

正向传播演算

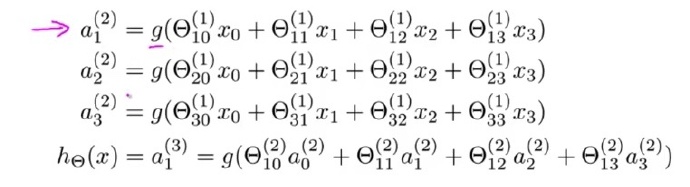
用简单的语言来表达就是：
上一层的输入乘上上一层到这一层的权重等于本层的神经元的输入
事实上我认为在一个神经网络中最重要的就是调整这些参数，那么有没有办法让参数的调整自动化呢？

什么是反向传播

反向传播就是有效的自动选择参赛的方式,我们来先来看看在机器学习中，自动参数选择机制是怎样运作的。
机器学习的目的是计算一个函数：

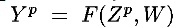
在这个公式中，Zp一个p维的输入模式，W代表系统中可调整的参数集，Yp可以代表Zp的分类标签，也可以代表每个属于某个类别的概率
loss函数（现在也叫cost函数）：

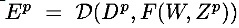
这个函数测量了Dp与Yp之间的误差。
我们只需要求min(Ep),也就是最小化误差便能得到最优的W。
而求最小化Ep的方法被称作梯度下降算法，一张图形容这个算法：

图中的像山一样的色彩区域描绘的是某个问题的所有W。
为了定位到山的最低点，我们随机从一个地方出发，然后小小朋友一样一步一步走下山，最终我们就会走到最低点（或者会是局部最低点）。
对于神经网络这个方法，我们依然使用了Cost函数和梯度下降来求最适合的W（也就是神经网络的权重集），但是为了实现这个计算我们便需要从最后一个神经元一路向前反溯才能实现这个算法，所以这个方法被称作反向传播神经网络，具体的实现如下：

神经网络的Cost Function

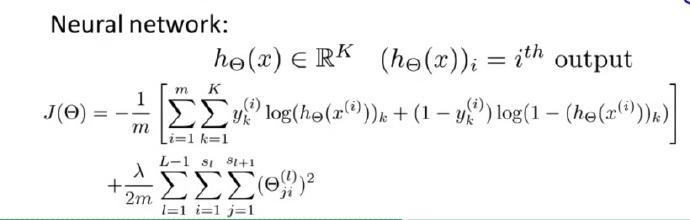
非常复杂的一个函数
对于这个公式的理解，稍后给出。
我们再来看一下前向传播的过程：

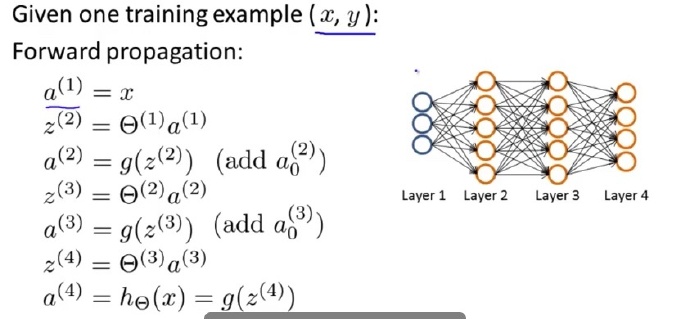
在反向传播里面，我们需要找到每个单元的误差，我们定义每个单元的误差为下：

每个误差的定义如下：

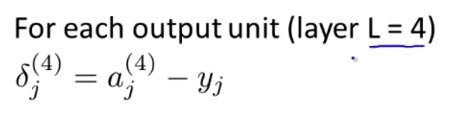
我们计算了最后一层的误差后，再往前反溯推倒其他层的误差

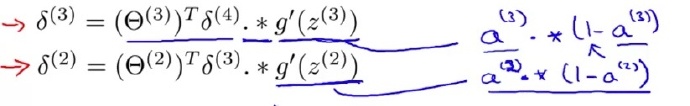
神经网络为什么会有效

卷积神经网络

(4.4,未完待续)