向题看齐408之数据结构DS概念记忆总结

Posted 2023-02-13 生命是有光的

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了向题看齐408之数据结构DS概念记忆总结相关的知识，希望对你有一定的参考价值。

408之数据结构DS概念记忆总结

1、线性表
2、栈和队列
3、串
4、树
4.1、树的性质
4.2、二叉树的性质
4.3、满二叉树的性质
4.4、线索二叉树的性质
4.5、二叉排序树的性质
4.6、平衡二叉树的性质
4.7、哈夫曼树的性质
4.8、树与森林的转换

5、图
5.1、顶点的度
5.2、连通与强连通
5.3、图的存储
5.4、图的遍历
5.5、最小生成树的构造
5.6、最短路径

6、查找
6.1、折半查找
6.3、红黑树
6.4、B树与B+树

7、排序
7.1、插入排序
7.1.1、直接插入排序
7.1.2、折半插入排序
7.1.3、希尔排序

7.2、交换排序
7.2.1、冒泡排序
7.2.2、快速排序

7.3、选择排序
7.3.1、简单选择排序
7.3.2、堆排序

7.4、归并排序
7.5、基数排序

1、线性表

算法原地工作的含义是：算法需要的辅助空间是常量，即O(1)
(在相同规模n下)，复杂度为O(n)的算法在时间上总是优于复杂度为O(n²)的算法。

$O(1)<O(log_2n)<O(n)<O(nlog_2n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$

时间复杂度：O(F(n))意味着算法在最坏情况下，问题规模为n的前提下，所花费的时间≤C×F(n)，其中C是常数。
- 某算法的时间复杂度为O(n²)，问题规模也是n，因为问题规模是在描述时间复杂度之前就已经规定好了。
- 某算法的时间复杂度为O(n²)，其实就是说算法的执行时间≤Cn²，也就是执行时间与n²成正比。
编译和解释可统称为翻译
- 编译：将高级语言编写的源程序全部语句一次全部翻译成机器语言程序，而后再执行机器语言程序（只需翻译一次，会产生中间文件）
- 解释：将源程序的一条语句翻译成对应于机器语言的语句，并立即执行。紧接着再翻译下一句（每次执行都要翻译，不会产生中间文件）
- 语言级别越高，执行效率越低。

算法的时间复杂度取决于：问题的规模和数据的状态(例如正序、逆序的数据元素)
- 加法规则：多项相加，只保留最高阶的项，且系数变为1 O(m)+O(n)=O(maxm,n)
- 乘法规则：多项相乘，都保留 O(m)×O(n)=O(mn)
线性表：相同数据类型、有限数据元素、序列
- 线性表可以为空
- 线性表中的元素可以是无序的
顺序表三大操作

操作	平均比较次数（平均移动元素）	时间复杂度
插入操作	n/2	O(n)
删除操作	(n-1)/2	O(n)
查找操作(按值查找)	(n+1)/2	O(n)

顺序表的元素地址必须是连续的，单链表的结点内存储单元地址必须是连续的。
- 单链表各个不同结点的存储空间可以不连续，但是结点内的存储单元地址必须连续(也就是data和next指针占有的空间必须是连续的)。
- 顺序表既可以顺序存取，也可以随机存取。链表只能进行顺序存取。
  - 随机存取：想取哪个就取哪个，通过数组下标进行访问
  - 顺序存取：从第一个开始访问，依次向后访问
- 链表插入和删除操作，只需要修改链表中结点指针的值，不需要移动元素就可以高效地实现插入和删除操作。链表采用链接方式存储线性表，适用于存储空间需求不确定的情形，不必事先估计存储空间。
- 顺序表就是数组，实现随机存取，并且在最后位置插入、删除方便。
  - n个元素的顺序表中，第i个结点是a[i-1]，最后一个结点是a[n-1]，之所以说在最后位置插入、删除方便，是因为最后一个结点的后面我们仍然可以直接访问到。
  - a【0】是首地址Loc(L)，则第n个元素地址 = 首地址Loc(L) + (n-1)×数据元素大小
- 链表和顺序表所需要的空间都与线性表长度成正比。
- 若要交换元素的值，例如交换第3个和第4个元素的值。在顺序表中，直接对3、4号元素的值进行更改，但是在链表中需要顺序访问1、2号元素的指针，才能找到3号数据的位置，进而再对3、4号元素的值进行修改。
- 若要顺序输出线性表的中的值，那么顺序表和链表都是顺序读取，时间复杂度都是O(n)
- 链式存储用指针表示逻辑结构，所以链式存储结构比顺序存储结构能更方便地表示各种逻辑结构，而顺序存储只能用物理上的邻接关系来表示逻辑结构。

// 双循环链表p后面跟一个就是指针，p后面跟两个就是结点的指针

// s的右指针指向p
s->rlink = p;
// s的左指针指向p的左指针指向(也就是两个指针指向相同)
s->llink = p->llink;
// s的左结点的右指针指向s
p->llink->rlink = s;


// p的下一个结点的前向指针指向p的前向指针的指向(也就是两个指针指向相同)
p->next->prev = p->prev;

做题画图必背🔥

顺序表：注意下标和位置的关系，例如有些题说在第i个位置插入元素，则i的范围为： 1≤i≤n+1，从第一个位置到第n+1个位置，n+1也就相当于在表尾追加。

不带头结点的单链表：

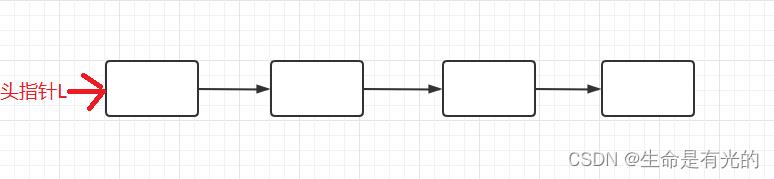
带头结点的单链表：

仅有尾指针的单链表：

带头结点的循环单链表：

带尾指针的循环单链表：

带头结点的双链表：

带头结点的循环双链表：

链表插入、删除的本质就是找前驱、后继，插入到哪个位置就找那个位置的前驱和后继，删除哪个位置就找那个位置的前驱和后继。
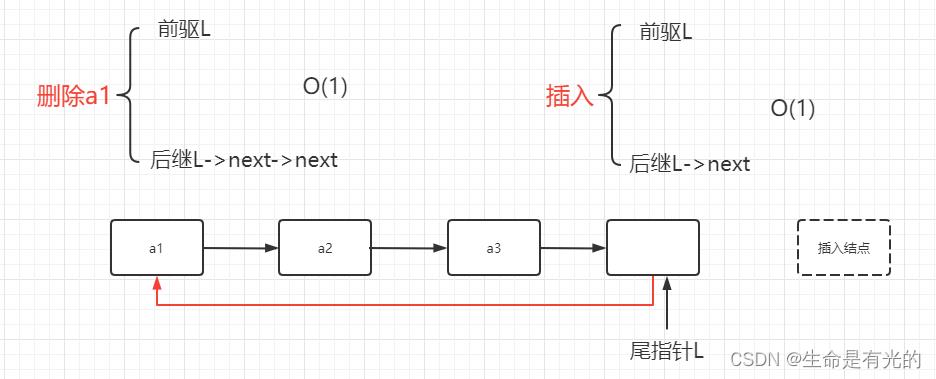
- 对于双向循环链表：前驱p->prev，后继p->next 都好找，所以必然插入、删除的时间复杂度为O(1)
- 在顺序表中删除第i个元素，或者在第i个元素之后插入新元素，时间复杂度都是O(n)
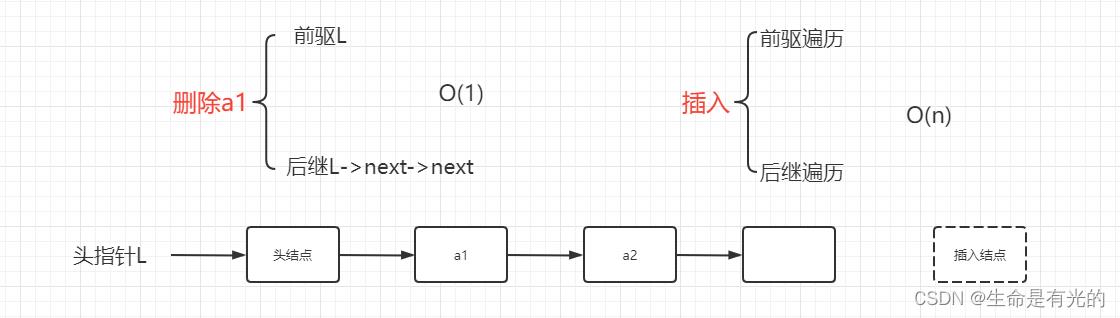
- 在链表中插入删除元素时间复杂度都是O(1)：❗注意❗，我们有时候在题中看到使用链表插入删除的时间复杂度为O(n)，这其实包含两个操作：查找这个结点：O(n)，删除这个结点：O(1)。所以我们常说链式存储方式能更快的实现插入和删除操作。
- 例如：在已知头指针的单链表中，要在尾部插入一个新结点和删除第一个元素，其时间复杂度为O(1)+O(n)
  
  删除第一个元素，就找第一个元素的前驱和后继。插入一个新结点，就找新结点位置的前驱和后继。

例如：在已知头指针的双链表中，要在尾部插入一个新结点和删除第一个元素，其时间复杂度为O(1)+O(n)

例如：在已知头指针的循环单链表中，要在尾部插入一个新结点和删除第一个元素，时间复杂度为O(1)+O(n)

例如：在已知尾指针的循环单链表中，要在尾部插入一个新结点和删除第一个元素，时间复杂度为O(1)

顺序表按值查找O(n)，按位查找O(1)，链表无论是按值还是按位查找都是O(n)
- 按值查找二者都是顺序查找，此时顺序表没有优势，二者查找效率相同。
- 按位查找顺序表是随机访问，效率更快，而链表只能顺序访问。
可以用 抽象数据类型ADT 来定义一个完整的数据结构。
- 抽象数据类型ADT包括 数据对象(数据)、数据关系、基本操作集
线性结构(一对一)：线性表、栈、队列、双队列、数组、串，非线性结构(非一对一)：二维数组、多维数组、广义表、树、图，顺序存储结构不仅可以存储线性结构，也可以存储非线性结构，例如树、图等。
有序表：关键字有序的线性表，仅描述元素间的逻辑关系，不在乎存储结构，因为只需要描述有顺序的逻辑即可。
- 所以属于逻辑结构的就是：有序表
- 有的题问哪个属于逻辑结构，也就是仅指定逻辑结构而不指定存储结构，只需要看题中是不是指定了存储结构。例如顺序表指定顺序存储，则描述了存储结构；哈希表指定散列存储，则描述了存储结构；单链表指定链式存储，则描述了存储结构；有序表顺序存储和链式存储均可，则未指定存储结构，属于逻辑结构
- 有的题问哪个属于存储结构，也就是仅指定存储结构而不指定逻辑结构，只需要题中是不是指定了存储结构。例如链表指定链式存储，则属于存储结构，哈希表指定散列存储，则属于存储结构。
存储数据时，不仅要存储各数据元素的值，而且要存储数据元素之间的关系。
计算时间复杂度问题：若内层外层没有关系，可以先算外层再算内层，然后相乘。若内层外层有关系，则通过外层来计算内层执行次数，最终将执行次数相加。
头指针为L，带头结点的单链表为空：L->next=null ，不带头结点的单链表为空：L=null
- 带头结点的双循环链表为空：L->prior ==L && L->next ==L ，头指针的前驱和后继都指向自身
在插入、删除操作中，双链表可以更容易找到前驱和后继，虽然花费的时间少了，但是因为修改了更多的指针指向，所以相比起单链表，操作更复杂了。相当于用更多的操作换取更少的时间。
静态链表
- 静态链表需要分配比较大的连续空间
- 静态链表在插入、删除元素时不需要移动元素，只需要修改指针

若题目中说"链表不带头结点，但是却有表头指针"，这个时候表头指针指向的是就是第一个数据元素。也就是：
1. 链表带头结点，同时有表头指针，此时表头指针指向的就是头结点。插入删除只能在头结点右边进行。
2. 链表不带头结点，但是有表头指针，此时表头指针指向的是第一个数据元素，插入删除在第一个数据元素左右两边均可执行。

头指针必有，有头结点就指向头结点；没头结点就指向第一个数据元素

2、栈和队列

栈只能在栈顶进行插入删除，具有先进后出
队列只能在队尾插入，在队头删除，具有先进先出
综合1和2，所以说栈和队列都是限制存取点的线性结构。
栈和队列都具有相同的逻辑结构，逻辑结构就是线性和非线性结构，二者都是线性结构。存储结构分为顺序存储和链式存储结构，二者均可实现顺序存储和链式存储。
顺序栈在插入、删除操作上比链栈复杂度更低，因为栈只能在栈顶进行插入、删除，而顺序表在表尾插入、删除的时间复杂度都是O(1)。栈的存取时间复杂度都是O(1)。链栈有一个比较明显的优势，那就是通常不会出现栈满的情况。

分析题画图必备🔥

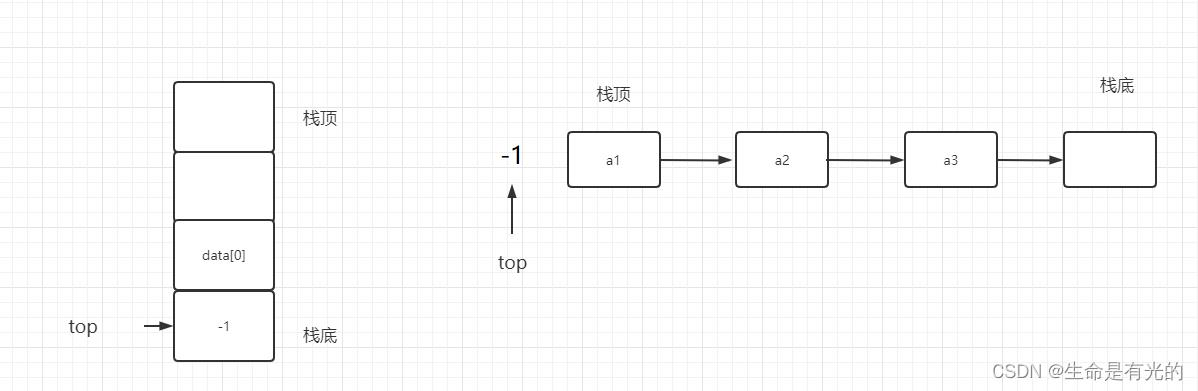
栈顶指针分为两种：一种是栈顶指针指向栈顶元素，另一种是栈顶指针指向栈顶元素的下一个位置

栈顶指针指向栈顶元素(也就是初值指向-1)。
- 这种情况下初始化：top=-1
- 这种情况下判断是否为空栈：判断top指针是否是-1
- 这钟情况下入栈：先让top++，然后将元素放入top所指向的 a1 处
- 这种情况下出栈：先让元素出栈，然后top- -
- 这种情况下栈满：top=MaxSize-1

栈顶指针指向栈顶元素的下一个位置
- 这种情况下初始化：top=0
- 这种情况下判断是否为空栈：判断top指针是否是0
- 这钟情况下入栈：先将元素a1放入top所指向的位置，然后 top++
- 这种情况下出栈：先让top- -，然后将元素出栈
- 这种情况下栈满：top=MaxSize

上述情况也适合不带头结点的链栈，对于带头结点的链栈：top指针指向的就是头结点

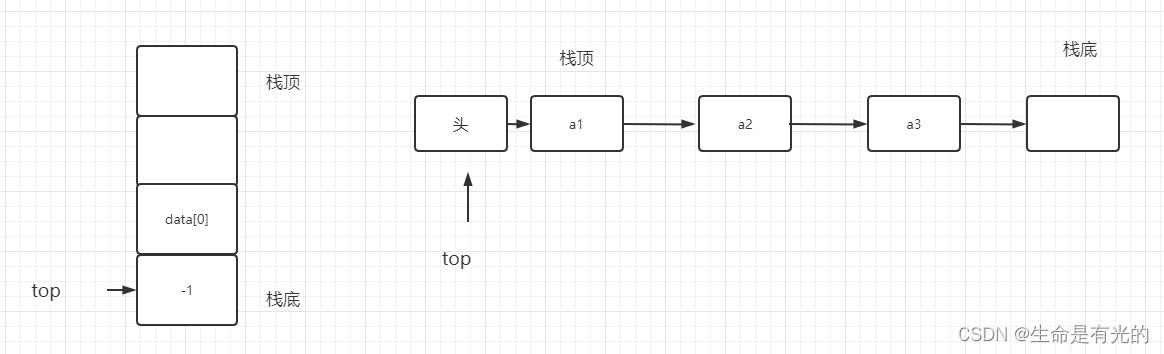
不带头结点的链栈，top指针指向第一个数据元素，带头结点的链栈，top指针指向头结点

共享栈的好处是：节省存储空间，降低发生上溢的可能
- 栈的空间是 0~预设空间上限，所以只可能发生上溢。
- 当第一个栈顶指针top1初值是-1，第二个栈顶指针top2初值为n。栈满的条件为top2-top1=1

当第一个栈顶指针top1初值是0，第二个栈顶指针top2初值为n-1。栈满的条件为top1-top2=1

队列有两种：一种是队尾指针 rear 指向队尾元素的下一个位置(循环队列)，一种是队尾指针指向队尾元素
1. 队头指针 front 指向队头元素，队尾指针 rear 指向队尾元素的后一个位置(下图红色单元不存储元素)
  - 初始化队列：队头、队尾指针指向0 rear = = front = = 0
  - 判断队列是否为空：队头、队尾指针是否指向0
  - 入队：将元素放入队尾指针所指向的位置，然后再将队尾指针rear向后移动一位(入队队尾指针rear++)，入队操作：(rear+1) % MaxSize 。【这里的MaxSize就是队列的最大容量，例如队列是数组A[0，n]，那么容量就为n+1】。所以队尾指针 rear 其实是从队头指向队尾，再从队尾指向队头，这样循环移动
  - 出队：front指针依次向后移动，当front指针和rear指针指向相同，则队列为空(出队队头指针front++)，出队操作：(front+1) ％ MaxSize
  - 队满的条件：队尾指针+1=队头指针 (Q.rear+1) % MAXSIZE == Q.front
  - 队空的条件：队尾指针和队头指针指向相同均指向0 Q.rear == Q.front ==0
  - 队列元素的个数：(队尾指针+最大队元素-队头指针)对最大队元素取余 (rear+MaxSize-front) % MaxSize
1. 队尾指针指向队尾元素
  - 初始化队列：队头指针指向0，队尾指针指向n-1的位置 rear = n-1， front = 0
  - 判断队列是否为空：队尾指针的下一个位置是不是队头指针 (rear+1) % MaxSize = front
  - 入队：队尾指针rear++，然后放入元素。入队操作：(rear+1) % MaxSize 。
  - 出队：front指针依次向后移动，当front指针和rear指针指向相同，则队列为空(出队队头指针front++)，出队操作：(front+1) ％ MaxSize
  - 队满的条件：队尾指针+2=队头指针 (Q.rear+2) % MAXSIZE == Q.front
  - 队空的条件：队尾指针的下一个位置指向队头 (rear+1) % MaxSize = front
上述两种情况都是牺牲一个存储单元，牺牲的都是队尾的最后一个单元。

也有些题牺牲队头的第一个单元，例如循环队列，front指向队头元素的前一个位置1，rear指向队尾元素，这种情况下牺牲的就是第一个单元。【王道队列选择第6题】
当然对于上述循环队列判断队满，有三种方式可以判断
1. 方案一：浪费一个存储单元
  - 队满的条件：队尾指针+1=队头指针 (Q.rear+1) % MAXSIZE == Q.front
  - 队空的条件：对尾指针和队头指针指向相同 Q.rear == Q.front
  - 队列元素的个数：(队尾指针+最大队元素-队头指针)对最大队元素取余 (rear+MaxSize-front) % MaxSize
2. 方案二：不浪费一个存储单元，用一个 size
  - 队空的条件：size值为0，因为size表示队内元素个数 Q.size == 0
  - 队满的条件：size值等于最大队元素 Q.size == MaxSize
3. 方案三：不浪费存储单元，用一个 tag 标记
  - tag=0时，若因删除导致Q.rear==Q.front,则为队空
  - tag=1时，若因插入导致Q.rear==Q.front,则为队满

栈的应用
- 中缀转后缀手算：根据左优先确定中缀表达式的运算符的先后顺序，按照 [左操作数右操作数运算符] 的方式组合成一个新的操作数【真题没考过】

中缀转后缀机算：从左到右扫描🔥【真题考过】
1. 遇到操作数。直接加入后缀表达式
2. 遇到界限符。遇到左括号 ( 直接入栈；遇到右括号 ) 则依次弹出栈内运算符并加入后缀表达式，直到弹出左括号( 为止。注意：左括号( 不加入后缀表达式。
3. 遇到运算符。依次弹出栈p中**优先级(乘除优先级高于加减)**高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到 ( 或栈空则停止。之后再把当前运算符入栈。

中缀转前缀手算：根据右优先确定中缀表达式的运算符的先后顺序，按照 [左操作数右操作数运算符] 的方式组合成一个新的操作数【真题没考过】
后缀转中缀：从左往右扫描，每遇到一个运算符，就让运算符插入前面最近的两个操作数之间，然后操作数两边带上括号【真题没考过】

后缀表达式手算：给你一个后缀表达式，计算它的值。从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数。【真题没考过】
后缀表达式机算【真题考过】
1. 从左往右扫描下一个元素
2. 若扫描到操作数则压入栈
3. 若扫描到运算符，则弹出两个栈顶元素，执行运算符运算，运算结果压回栈顶。
中缀表达式机算：初始化两个栈，操作数栈和运算符栈。🔥
1. 若扫描到操作数，则压入操作数栈
2. 若扫描到运算符或界限符，则按照 “中缀转后缀” 相同的逻辑压入运算符栈(期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈)

栈的应用：

递归
- 函数执行顺序为 main()函数->A函数->B函数，则从栈底到栈顶依次为 main()->A->B
- 函数调用时，将调用返回地址、实参、局部变量都会存在栈中
进制转换
迷宫求解
括号匹配

队列的应用：

缓冲区：打印机缓冲区等
- 但是有一个缓冲区不是队列：输入缓冲区。(输入账号密码那个框，是后进先出)
页面置换算法

3、串

串的存储方式有两种，顺序存储和链式存储，顺序存储由分为定长存储和堆分配存储(可以改变大小)。
串的模式匹配：在主串中找到与模式串相同的子串，并返回其所在位置。
朴素模式匹配算法(简单模式匹配算法)思想：将主串中的模式串长度相同的子串搞出来，挨个与模式串对比，当子串与模式串某个对应字符不匹配时，就立即放弃当前子串，转而检索下一个子串
若模式串长度为 m，主串长度为 n，则直到匹配成功/匹配失败最多需要 (n-m+1)*m 次比较
- 最坏时间复杂度：O(nm)
- 最坏情况：每个子串的前 m-1 个字符都和模式串匹配，只有第 m 个字符不匹配
- 比较好的情况：每个字符的第一个字符就与模式串不匹配，长度为 n 的主串中有 n-m+1 个长度为 m 的子串，每个子串只需要对比一个字符，所以匹配失败的最好时间复杂度为：O(n-m+1)= O(n-m) ≈ O(n)

朴素模式匹配算法的缺点：当某些子串与模式串能部分匹配时，主串的扫描指针i经常回溯，导致时间开销增加。最坏的时间复杂度O(nm)

KMP算法：当子串和模式串不匹配时，主串指针i不回溯，模式串指针 j=next[j] ，算法的平均时间复杂度：O(n+m)

KMP算法：

对于串'abaabc' ，若 next数组第一位是-1，则序号从0开始，next数组 = 最长前后缀相等长度

序号	0	1	2	3	4	5
模式串	a	b	a	a	b	c
next数组	-1

对于串'abaabc' ，若 next数组第一位是0，则序号从1开始，next数组 = 最长前后缀相等长度 + 1

序号	1	2	3	4	5	6
模式串	a	b	a	a	b	c
next数组	0

搞懂next数组存在的意义，当匹配失败时，模式串的指针指向next数组处。

例如主串T='abaabaabcabaabc'，模式串为 'abaabc' ，采用KMP算法进行模式匹配

序号	0	1	2	3	4	5
模式串	a	b	a	a	b	c
next数组	-1	0	0	1	1	2

设序号从0开始，指针i指向主串，指针j指向模式串，当第一次匹配失败时，i=j=5，下一次匹配时主串的指针i不动，j跳转指向next[j]=next[5]=2处，也就是j=2。说明接下来模式串从abaabc 从第3个a开始和主串匹配
第一次匹配比较6次，第二次匹配只需比较4次，总共比较10次就可以匹配成功

4、树

度为2的树和二叉树的区别：

度为2的树和二叉树的每个结点都最多只能有两个孩子。
度为2的树至少有一个结点的度是2，但是二叉树允许所有结点的度都小于2。
度为2的树一定是非空树，至少有2+1=3个结点。二叉树可以为空树。

二叉树是有序树，即使树中结点只有一棵子树，也要区分它是左子树还是右子树。

度为2的有序树就是二叉树。（×）在二叉树中，若某个结点只有一个孩子，则这个孩子的左右次序是确定的，而在度为2的有序树中，若某个结点只有一个孩子，则这个孩子就无序区分左右次序。

树的结点数为n，边数是n-1，再添一条边一定会形成一个环。
n 个结点的二叉树，有 n + 1 个空链域。我们可以利用这些空链域来记录前驱、后继的信息。
- 理解一：n个结点，共有2n个指针，有n-1条边(用掉n-1条指针)，则还剩空指针 2n-(n-1)=n+1
- 理解二：线索只能由 n₀、n₁构成，n₀提供两条线索，n₁提供一条线索，2n₀+n₁ = n₀+(n₂+1)+n₁=n+1
对于任何一棵二叉树，高度可能为 ⌈ log₂ (n+1)⌉ ~ n 或 ⌊log₂ n⌋ + 1 ~ n
- 完全二叉树的高度最小为 ⌈ log₂ (n+1)⌉ 或 ⌊log₂ n⌋ + 1
- 高度最高就是每层一个结点，共n层
若二叉树采用二叉链表结构，则链表中只有孩子结点的地址，而无双亲结点的地址，而遍历过程中又需要结点的双亲结点的地址，为此，遍历操作设置一个栈来达到这个目的。如果不设置栈，则需要采用三叉链表结构，因此三叉链表中除了孩子结点的地址以外，还保存了结点的双亲结点的地址。
前序序列和后序序列不能唯一的确定一棵二叉树，但是可以确定二叉树中结点的祖先关系。当两个结点的前序序列为XY，后续序列为YX时，则X为Y的祖先。
- 例如前序序列为 a e b d c，后序序列为 b c d e a ，可知 a 为根结点，e 为 a 的孩子结点。
- 此外，由 a 的孩子结点的前序序列 e b d c，后序序列 b c d e，可知 e 是 b c d 的祖先

4.1、树的性质

树的性质：

结点数 = 总度数(总边数)+1
度为 m 的树第 i 层至多有 m^i-1 个结点
$假设每层都是满的 \\\\ 第一层m^0 \\\\ 第二层m^1 \\\\ 第三层m^2 \\\\ .... \\\\ 第i层m^i-1$
高度为 h 的 m 叉树至多有 (m^h -1)/(m-1) 个结点
$\\\\ m^0+m^1+m^2+...+m^h-1 = \\fracm^h-1m-1$
具有n个结点的m叉树的最小高度为
$\\\\ \\fracm^h-1m-1 = n \\\\ h=[log_m(n(m-1)+1)] \\\\ 之所以向上取整的原因是即使最后一层有一个结点也得算一个高度$

向题看齐408之计算机组成原理概念记忆总结

向题看齐408之计算机组成原理概念记忆总结

向题看齐408之计算机组成原理概念记忆总结

向题看齐408之操作系统OS概念记忆总结

向题看齐408之操作系统OS概念记忆总结