算法初步--递归思想(java实现)
Posted Heisenberg_Posion
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法初步--递归思想(java实现)相关的知识,希望对你有一定的参考价值。
文章目录
递归是我们学习算法最开始接触的一种思想,并且这种思想对我们学习其他算法也有很大的帮助,像快速排序,归并排序都用到了递归的思想
递归设计经验,找重复的部分,找重复中的变化量,设计出口,不然会一直循环
以求n的阶乘为例子,来感受下递归是怎样的
要求n的阶乘可以转成求n*(n-1)的阶乘,这样一个子问题,再细分,这就是找重复的部分,然后变化量是n,设计出口让循环结束,这里是当n=1时函数返回。
public static int calculateN(int n)
if (n==1)
return 1;
return n*calculateN(n-1);
简单的递归练习
package com.zjl.recursion;
/**
* @author 朱佳林
* @version 1.0
* @englishName jack
*/
public class CalculateN
public static void main(String[] args)
// System.out.println(calculateN(3));
// printItOJ(5,10);
// int[]arrayTest=1,2,3,4,5,6,7,8,9,10;
// System.out.println(sumArray(arrayTest,0));
System.out.println(reverse("iMissYou"));
//计算n的阶乘
public static int calculateN(int n)
if (n==1)
return 1;
return n*calculateN(n-1);
//打印i ~ j
public static void printItOJ(int i,int j)
if (i>j)
return;
System.out.println(i);
printItOJ(i+1,j);
//数组求和
public static int sumArray(int[] array,int index)
if (index==array.length-1)
return array[index];
return array[index]+sumArray(array,index+1);
//翻转字符串
//最后一个字符+翻转前面的字符串得到的字符
public static String reverse(String temp)
if (temp.length()==1)
return temp;
return temp.charAt(temp.length()-1)+reverse(temp.substring(0,temp.length()-1));
斐波拉契数列,求第n项的数。
斐波拉契是转换为了多个分支
public class Fibonacci
public static void main(String[] args)
int result=calculateFibonacci(5);
System.out.println(result);
public static int calculateFibonacci(int n)
if (n==1||n==2)
return 1;
return calculateFibonacci(n-1)+calculateFibonacci(n-2);
最大公约数
数学问题一般是找递推公式,像上面的斐波拉契数列f(n)=f(n-1)+f(n-2)
最大公约数的递推公式是gcd(m,n)=gcd(n,m%n);
这个递推公式的理解,默认前者更小,如果更大也没关系,取余之后也会被换过来
m,n == kn+b ,这个b就是取余后的结果,假如p是 n和kn+b的最大公约数,那么p能整除n,并且b也要整除p,举个例子2和2*3+5,如果5不能整除最大公约数2,那么最大公约数就不可能是2,那么5也就是b一定要整除最大公约数
那么就可以得到上面的递推公式gcd(m,n)=gcd(n,m%n),取余的结果就是那个b
public class GCD
public static void main(String[] args)
System.out.println(gcd(28,6));
public static int gcd(int m,int n)
if (m%n==0)
return n;
return gcd(n,m%n);
通过递归形式进行插入排序
以递归形式作插入排序,也是分为子问题,先假设已对前面k-1个数进行排序,再将最后一个数插入到合适位置
public static void recursionInsertSort(int[] array,int k)
if (k==0)
return;
//对数组的k-1个数进行排序,再将最后一个数插入到它该存在的位置
recursionInsertSort(array,k-1);
int x=array[k];
int index=k-1;
while (index>-1&&x<array[index])
array[index+1]=array[index];
index--;
array[index+1]=x;
经典递归问题–汉诺塔
关于汉诺塔问题,可以参考我另外一篇博客,自认为是讲的比较清楚的,只不过是用c++实现的,不过没什么关系,能看懂核心代码就行。
不会还有人看了我的教程不会汉诺塔问题的解法吧!_Hensenberg的博客-CSDN博客_河内塔问题解决策略
public class HanoT
public static void main(String[] args)
int result=hanoT(4,'a','b','c');
System.out.println(result);
public static int hanoT(int n,char a,char b,char c)
if (n==0)
return 0;
if (n==1)
return 1;
return hanoT(n-1,a,c,b)+1+hanoT(n-1,b,a,c);
二分查找的递归解法
递归与斐波拉契不同的是它有两条路,它只会选择一条路递归下去
public class BinarySearch
public static void main(String[] args)
int[]arr=1,4,8,26,56;
System.out.println(binarySearch1(arr,0,4,8));
public static int binarySearch1(int[]array,int low,int high,int key)
if (low>high)
return -1;
int mid=low+(high-low)>>1;
int midVal=array[mid];
if (key<midVal)
return binarySearch1(array,low,mid-1,key);
else if (key>midVal)
return binarySearch1(array,mid+1,high,key);
return mid;
二分查找的时间复杂度是o(lgn) ,顺序查找是o(n)
递归形式的算法分析
子问题的规模下降
子问题的答案约处理的时间
以计算阶乘举例
T(n)=T(n-1)+O(1);
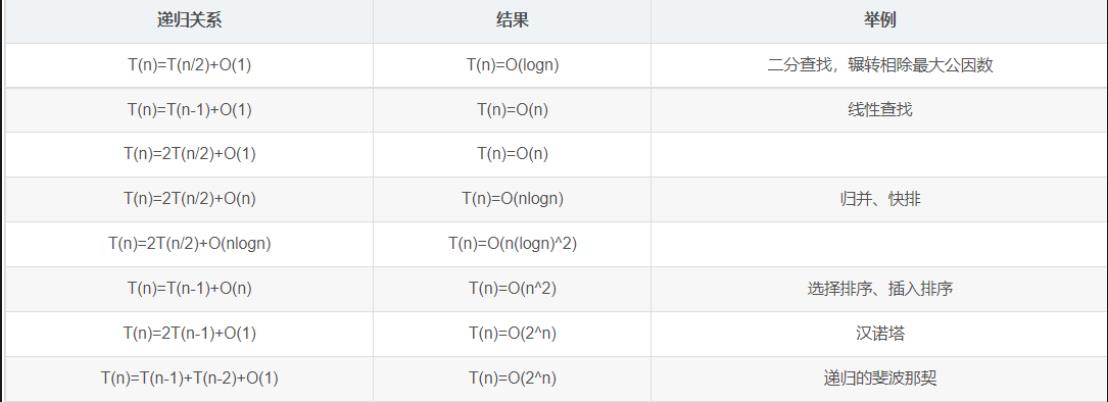
对递归做一个总结,像阶乘就是普通的递归,斐波拉契和二分查找是一个数学式子的递归,汉诺塔是带有选择的递归,二分查找是从两条路中选择一条路递归下去
小白登台阶
package com.zjl.recursion;
/**
* @author 朱佳林
* @version 1.0
* @englishName jack
*/
public class UpStairs
public static void main(String[] args)
System.out.println(upStairs(30));
public static int upStairs(int n)
if (n==1)
return 1;
if (n==2)
return 2;
if (n==3)
return 4;
return upStairs(n-1)+upStairs(n-2)+upStairs(n-3);
public static int upStairs2(int n)
if (n==1)
return 1;
if (n==2)
return 2;
return upStairs(n-1)+upStairs(n-2);
在有空字符串的数组中查找字符串
就是二分查找的变形,这题主要是能够知道如何对空字符串进行处理,用while循环使中间字符串不为空,并且得是mid++,而不能–,举例 0 1,得到mid=0,只能+1,而不能-1
public class FindString
public static void main(String[] args)
String[] tes="abc","","back","","second","zone","zu";
System.out.println(findString(tes,"abc"));
public static int findString(String[] strings,String string)
int begin=0;
int end=strings.length-1;
while (begin<end)
int mid=begin+(end-begin)>>1;
while (strings[mid].equals(""))
mid++;
if (string.compareTo(strings[mid])<0)
end=mid-1;
else if (string.compareTo(strings[mid])>0)
begin=mid+1;
else return mid;
return -1;
最长连续递增子序列(部分有序)
(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)。
这个比较简单,看一下就会了
package com.zjl.recursion;
import java.util.Arrays;
/**
* @author 朱佳林
* @version 1.0
* @englishName jack
*/
public class LongestOrder
public static void main(String[] args)
int []tes =1,9,2,5,7,3,4,6,8,0;
System.out.println(findLongest(tes));
System.out.println(Arrays.toString(longestOrder(tes)));
public static int[] longestOrder(int[] array)
int maxLength=1;
int begin=0;
int end=0;
int tempLength=1;
int j=0;
for (int i = 0; i < array.length; i++)
tempLength=1;
for (j = i; j <array.length-1 ; j++)
if (array[j+1]>=array[j])
tempLength++;
else break;
if (tempLength>maxLength)
maxLength=tempLength;
begin=i;
end=j;
return Arrays.copyOfRange(array,begin,end+1);
public static int findLongest(int []array)
int count=1;
int maxLength=1;
for (int i = 0; i < array.length - 1; i++)
if (array[i+1]>=array[i])
count++;
else
maxLength=Math.max(count,maxLength);
count=1;
return maxLength;
以上是关于算法初步--递归思想(java实现)的主要内容,如果未能解决你的问题,请参考以下文章