吴恩达_MIT_MachineLearning公开课ch05

Posted 2023-02-05 用七年单身换个PolyU.CSPhD

回顾神经网络

ch04我们实现了属于自己的神经网络。
一个完整的神经网络需要一个模型表示，比如网络层数及每一层的神经元个数。除此之外我们要保证网络的流动性，即实现前向传播和反向传播。
前向传播是比较简单的，即进行矩阵运算以及sigmoid激活函数处理。
反向传播需要用到链式求导法则，同时要求中间“误差”δ，需要自己好好理解。

将数据进行切分

我们按照惯例会把手上的数据按照6:2:2的比例划分成—训练集、可行集、测试集，英文分别为train、cross validation、test。

why？其实回想一下我们之前做手写数字分类的作业，我们训练时将5000条数据扔进去拟合出theta，最后predict的时候同样是这5000条数据。
(当然，我们的神经网络训出来的泛化性应该是很不错的！只是针对这种做法批判)
这就存在了很大的问题，train和test用的同一组，那我们根本不知道其在新数据上的表现。说白了如果计算机傻一点像一本字典一样把一张图对应一个标签全部存下来，那最后的预测率就是恐怖的100%了，但放到新数据上可能低得离谱。

我们在训练数据时还有一个较重要的参数是learning_rate，我们会在作业中学会画出validation_error关于learning_rate的折线从而找到最小的error决定采用某个lr。

所以对于这三个集合我们的理解如下：
训练集仍然是用于训练拟合出theta的，然后我们带着这个theta调试不同的learning_rate找到令validation_error最小的rate，自此我们得到了theta和最优lr，代入计算test_error作为模型最后的正确率的体现！

Bias & Variance

本章就是围绕bias和variance展开的。
在我们的概念里这两个单词的含义应该是“偏置”、“方差”，但在机器学习中他们分别代表了“欠拟合”、“过拟合”。

Andrew在视频里着重教我们分析自己的模型存在以上的哪一种问题。
无疑机器学习是需要大量训练数据的，但如果你的模型表达本身就存在较大的问题，那么海量的数据也无法帮到你，最后的损失值依旧会非常高！
我们主要分析以下几种办法对于模型泛化性提升的帮助：
得到更多的训练数据、
添加更多的特征、
筛选特征，缩减一些特征、
将已有特征做一个多项式处理，扩维、
降低学习率、
提高学习率。

依次写出上面的方法是针对哪类问题的解决策略：
过拟合(对已有数据集拟合太出色导致泛化性不好，要更多地数据！)、
欠拟合(这个应该不难理解，其实和特征做多项式处理是同源的！)、
过拟合(显然的，上者的反面)、
欠拟合(就好比我们的作业中一开始用线性拟合效果是不好的，欠拟合的，所以我们扩维到8次方！)、
欠拟合(因为learning_rate太高，导致我们的正则项损失很大，夸张一点最后可能一些高次项[甚至一次项]都会被惩罚得很厉害，导致theta趋近于0，除了bias的那个theta，那么最后会画出来一条平的线，欠拟合会很厉害，所以要降低lr！)、
过拟合(上者的反面)。

如果我讲得不是很清楚建议直接去看Andrew的视频。
机器学习–吴恩达，p61-p64。

作业

其实作业里的函数都是之前用过的。
costFunction，Gradient，mapFeatures等等都是早已实现过的，应该是不难理解。
可能唯一没做过的就是Normalization了。

作业的第二大部分要求你特征映射到8次方进行拟合，画出learning_curve，根据图中valid_error和train_error的关系来判定自己的模型出了什么问题。

对于learning_curve的简要分析：
如下所示是一张自己搞出来的图，其横坐标是数据量，纵坐标是总误差。也就是说我们每次仅从train_set中提取m条数据进行拟合，得到结果后求总误差。

欠拟合时无论train_error和valid_error都是比较大的，但前者有上升趋势同时后者有下降趋势。最后随着数据量不断增加，两者趋于稳定。

下图是我跑出来的过拟合学习曲线：

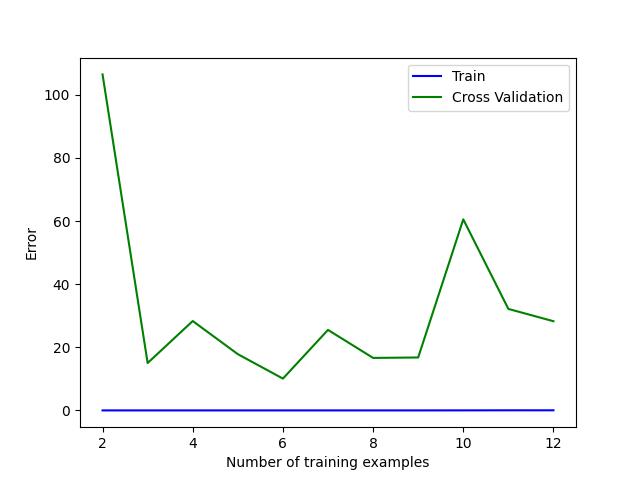
一个较为典型的特征就是train_error基本趋于0，很好理解，因为模型将给出的训练数据用高次项拟合得非常出色导致在训练集上基本无误差，但在valid_error上就会和train_error存在一个较大的gap。因为模型太复杂，泛化性也是不强的。

作业的后面还会让你调整learning_rate画出不同曲线等，自己去跑就行。

在主函数中一段一段打开完成某一个特定任务，同时注意visualize函数中的plt.show后面的注释，有时候需要打开否则因为坐标原因图形畸变比较厉害！

import matplotlib.pyplot as plt
import numpy as np
from scipy.io import loadmat
import scipy.optimize as opt
import matplotlib.pyplot as plt


def visualization():
    Data = loadmat("./ex5data1.mat")
    X, y, Xtest, ytest, Xval, yval = Data['X'], Data['y'], Data['Xtest'], Data['ytest'], Data['Xval'], Data['yval']
    # after debugging, you may find the Dictionary(Data) contains mainly the above data
    # if you have watched the video, you should know we separate the whole data into three parts:
    # train, cross validation, test    for different use
    # X & y are training data      Xval & yval are cross validation data
    # the corresponding size is (12, 1)train ----  (21, 1)validation ---- (21, 1)test
    plt.scatter(X, y, marker='x', c='red')
    plt.xlabel('Change in water level (x)')
    plt.ylabel('Water flowing out of the dam (y)')
    # plt.show()   # if you are doing the last 2 tasks, please delete the signal '#' before "plt.show()"
    return X, y, Xtest, ytest, Xval, yval


def costFunction(theta, X, y, lr):
    bias = np.ones((X.shape[0], 1))
    x = np.hstack((bias, X))  # size is (12, 2)
    # the shape of theta is (2, )
    cost = np.mean(np.power(np.dot(x, theta.reshape(-1, 1)) - y, 2)) / 2
    reg_cost = np.sum(np.multiply(theta[1:], theta[1:])) * lr / (2 * X.shape[0])
    cost += reg_cost
    # the initial cost is 303.993, which is same as Andrew Ng had given! It's verified!
    return cost


def calGradient(theta, X, y, lr):
    bias = np.ones((X.shape[0], 1))
    x = np.hstack((bias, X))
    grad = np.zeros(theta.shape)
    loss = np.dot(x, theta.reshape(-1, 1)) - y
    for i in range(x.shape[1]):
        grad[i] = np.mean(loss * x[:, i].reshape(-1, 1))
    grad[1:] += lr * theta[1:] / X.shape[0]
    # after debugging, you will find it's true
    # because the initial gradient is [-15.30, 598.250]
    return grad


def fminc_linear(theta, X, y, lr):
    result = opt.minimize(fun=costFunction, x0=theta, method='BFGS', args=(X, y, lr), jac=calGradient)
    theta = result['x']
    # print(result)
    return theta


def drawResult_linear(theta, X, y):
    x_labels = [np.min(X), np.max(X)]
    xx = np.array([[1, x_labels[0]], [1, x_labels[1]]])
    yy = np.dot(xx, theta.reshape(-1, 1))
    y_lables = [yy[0, 0], yy[1, 0]]
    plt.plot(x_labels, y_lables, c='blue')
    plt.xlabel('Change in water level (x)')
    plt.ylabel('Water flowing out of the dam (y)')
    plt.show()


def drawResult(theta, X, y):
    X = np.sort(X, axis=0)
    x_labels = np.linspace(-50, 50, 100)
    XX = np.array(x_labels).reshape(-1, 1)
    XX = polyFeatures(XX, 8)
    XX = featureNormalization(XX)
    bias = np.ones((XX.shape[0], 1))
    temp = np.hstack((bias, XX))
    YY = np.dot(temp, theta.reshape(-1, 1))
    plt.plot(x_labels, YY, linestyle='--')
    plt.xlabel('Change in water level (x)')
    plt.ylabel('Water flowing out of the dam (y)')
    plt.show()


def jErrorCost(theta, X, y):
    # this cost is without reg_cost
    bias = np.ones((X.shape[0], 1))
    x = np.hstack((bias, X))
    cost = np.mean(np.power(np.dot(x, theta.reshape(-1, 1)) - y, 2)) / 2
    return cost


def separateTrainingSet_linear(X, y, Xval, yval, lr):
    loss_train = []
    loss_val = []
    for i in range(X.shape[0]):
        X_train = X[0:i + 1, :]
        y_train = y[0:i + 1, :]
        theta = np.ones(X.shape[1] + 1)
        theta = fminc_linear(theta, X_train, y_train, lr)
        loss_train.append(jErrorCost(theta, X_train, y_train))
        loss_val.append(jErrorCost(theta, Xval, yval))
    drawLearningCurves(loss_train, loss_val, 0)


def separateTrainingSet_poly(X, y, Xval, yval, lr):
    loss_train = []
    loss_val = []
    Xvalid = polyFeatures(Xval, 8)
    Xvalid = featureNormalization(Xvalid)
    for i in range(1, X.shape[0]):
        X_train = X[0:i + 1, :]
        y_train = y[0:i + 1, :]
        X_train = polyFeatures(X_train, 8)
        X_train = featureNormalization(X_train)
        theta = np.ones(X_train.shape[1] + 1)
        theta = fminc_linear(theta, X_train, y_train, lr)
        loss_train.append(jErrorCost(theta, X_train, y_train))
        loss_val.append(jErrorCost(theta, Xvalid, yval))
    drawLearningCurves(loss_train, loss_val, 1)


def polyFeatures(X, degree):
    temp = X.copy()
    for i in range(2, degree + 1):
        X = np.hstack((X, np.power(temp, i)))
    return X


def drawLearningCurves(loss_train, loss_val, start):
    x_labels = [i + 1 + start for i in range(len(loss_train))]
    plt.plot(x_labels, loss_train, c='blue', label='Train')
    plt.plot(x_labels, loss_val, c='green', label='Cross Validation')
    plt.legend()
    plt.xlabel("Number of training examples")
    plt.ylabel("Error")
    plt.show()


def featureNormalization(X_train):
    X_mean = np.mean(X_train, axis=0)
    X_std = np.std(X_train, axis=0)
    for i in range(X_train.shape[1]):
        X_train[:, i] = (X_train[:, i] - X_mean[i]) / X_std[i]
    return X_train


def validationCurve(X, y, Xval, yval):
    lr_list = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
    loss_list_val = []
    loss_list_tra = []
    Xvalid = polyFeatures(Xval, 8)
    Xvalid = featureNormalization(Xvalid)
    X_train = polyFeatures(X, 8)
    X_train_norm = featureNormalization(X_train)
    for lr in lr_list:
        theta = np.ones(X_train.shape[1] + 1)
        theta = fminc_linear(theta, X_train_norm, y, lr)
        loss_list_tra.append(costFunction(theta, X_train, y, lr))
        loss_list_val.append(costFunction(theta, Xvalid, yval, lr))
    plt.plot(lr_list, loss_list_tra, c='blue', label='Train')
    plt.plot(lr_list, loss_list_val, c='green', label='Cross Validation')
    plt.xlabel('lamda')
    plt.ylabel('Error')
    plt.legend()
    plt.show()


if __name__ == "__main__":
    X, y, Xtest, ytest, Xval, yval = visualization()

    """
    # because they're all verified, so there is no need to run them
    theta1 = np.ones(X.shape[1] + 1)
    costFunction(theta1, X, y, 1.0)
    calGradient(theta1, X, y, 1.0)
    """

    """
    theta1 = np.ones(X.shape[1] + 1)
    theta = fminc_linear(theta1, X, y, 1.0)
    drawResult_linear(theta, X, y)
    # linear function is not suitable to the data
    """

    """
    # the following code is to draw the learning curve of the linear model which is too simple
    separateTrainingSet_linear(X, y, Xval, yval, 1.0)
    """

    """
    # the following code firstly extend the features and then normalize the features
    # at last we use the trained parameters theta to draw the result
    X_train = polyFeatures(X, 8)
    X_train_norm = featureNormalization(X_train)
    theta = np.ones(X_train.shape[1] + 1)
    theta = fminc_linear(theta, X_train_norm, y, 0)
    drawResult(theta, X, y)
    """

    """
    # show learning curve 
    separateTrainingSet_poly(X, y, Xval, yval, 0)
    """

    """
    # try lamda = 1
    X_train = polyFeatures(X, 8)
    X_train_norm = featureNormalization(X_train)
    theta = np.ones(X_train.shape[1] + 1)
    theta = fminc_linear(theta, X_train_norm, y, 1.0)
    drawResult(theta, X, y)

    separateTrainingSet_poly(X, y, Xval, yval, 1.0)
    """

    """
    # try lamda = 100
    X_train = polyFeatures(X, 8)
    X_train_norm = featureNormalization(X_train)
    theta = np.ones(X_train.shape[1] + 1)
    theta = fminc_linear(theta, X_train_norm, y, 100.0)
    drawResult(theta, X, y)

    separateTrainingSet_poly(X, y, Xval, yval, 100.0)
    """

    """
    # the following code helps you automatically select the best lamda
    validationCurve(X, y, Xval, yval)
    # after looking, I find that setting learning rate to 0.3 is appropriate 
    """

    """
    # the following code is to calculate the error of test set
    X_train = polyFeatures(X, 8)
    X_train_norm = featureNormalization(X_train)
    theta = np.ones(X_train.shape[1] + 1)
    theta = fminc_linear(theta, X_train_norm, y, 0.3)
    Xtest = polyFeatures(Xtest, 8)
    Xtest = featureNormalization(Xtest)
    test_error = costFunction(theta, Xtest, ytest, 0.3)
    print("error on test set is: %f" % test_error)
    """
    exit(0)

比如这里展示一张validationCurve函数绘制出的图像：
根据此图，我们把鼠标移到绿线的最低点时你会发现learning_rate取0.3是较好的。

小结

总体来说这章不困难，作业里的代码也基本就是复用前些章节的所以较简单。
主要是学会如何诊断你的模型，如何学会观察learning_curve，最后如何解决模型现存的一些问题。

但是，但是！我的结果图和Andrew作业里给出的不是特别一致，我看网上好像也千奇百怪，版本繁多，但总体趋势感觉没有很多问题，并不是很乐意在这方面debug太久，就这样了！