CMOS开关_参数提取

Posted 2023-02-05 硬件老钢丝

参考文章一：硅基射频开关集成电路设计 许清河

SOI 开关晶体管等效模型

对论文中的内容进行粘贴学习，并未进行验证。

  SOI 晶体管模型采用了BSIM 内核，BSIM 全称为伯克利短沟道IGFET 模型，它是伯克利加州大学开发的基于物理的，准确的，可扩展的，稳健的和可预测的晶体管SPICE 模型。广泛应用于电路仿真和CMOS 技术开发。基于BSIM 内核的晶体管模型具备强大的仿真能力，其覆盖了从小信号到大信号，从直流到交流各种复杂仿真环境。

  虽然BSIM 模型易用，但它是由一组组复杂的公式以及相关的上百个参数组合而来，对射频工程师关心的晶体管内部寄生状况无法直观展现，当然这也因为晶体管高阶模型无法用简单的寄生元件替代描述。由于开关晶体管没有工作在放大区域，其特征表现与无源器件更为接近，因此可以对PDK 提供的晶体管模型用RC集总元件网络进行等效。这样等效的好处是可以直观地了解晶体管导通电阻、关闭电容与晶体管栅宽的关系，方便后续开关电路分析设计。

1、晶体管导通等效模型

  开关晶体管导通状态时，最简单的等效模型是等效成一个电阻。由于寄生电容容值较小，低频时容抗较大，简易模型忽略了各端口间的寄生电容。为了解各寄生元件相对量的大小以获得更为完整的模型。有必要对PDK 提供的晶体管模型进行寄生参数提取。

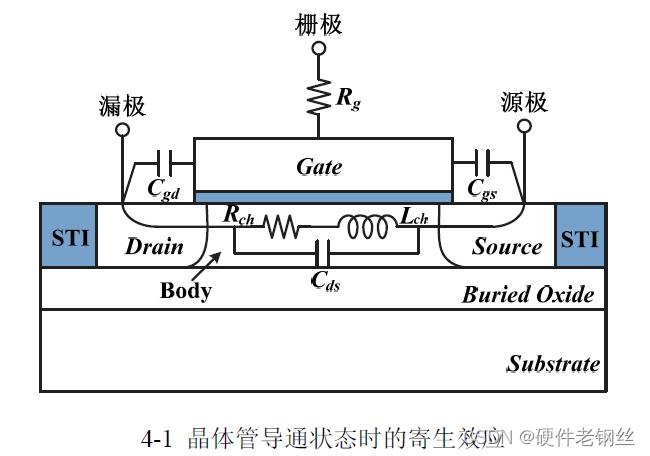
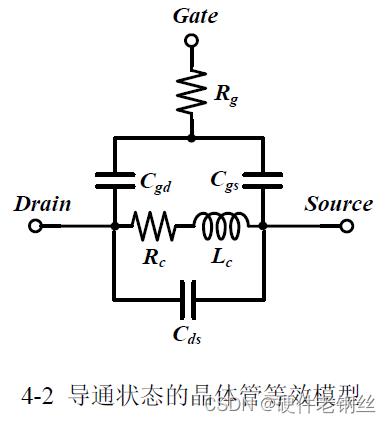
  导通状态的晶体管寄生效应如图4-1 所示，Rg 为栅极多晶硅寄生电阻，Cgd、Cgs 分别为栅漏、栅源寄生电容，Rc、Lc 分别为沟道导通电阻、电感，Cds 为漏源区寄生电容。等效模型见图4-2，值得注意的是由于PDK 提供的是裸管模型，不包含漏源金属连线及更上层金属的寄生参数，因此该等效模型忽略了漏极与源级的寄生电阻Rd 与Rs。

  确定模型的寄生元件以后，选取晶体管进行仿真，并提取寄生参数。这里选择的是SOI PDK 提供的厚栅管，单指栅宽为Wf = 10 μm，指数nf = 2，栅长L = 0.32μm。寄生参数提取需要对晶体管进行两步仿真。第一步仿真用于提取元件Rc、Lc、Cgd、Cgs 与Cds 的值，仿真原理图如图4-3（a）所示，仿真等效集总模型网络见图4-3（b）。



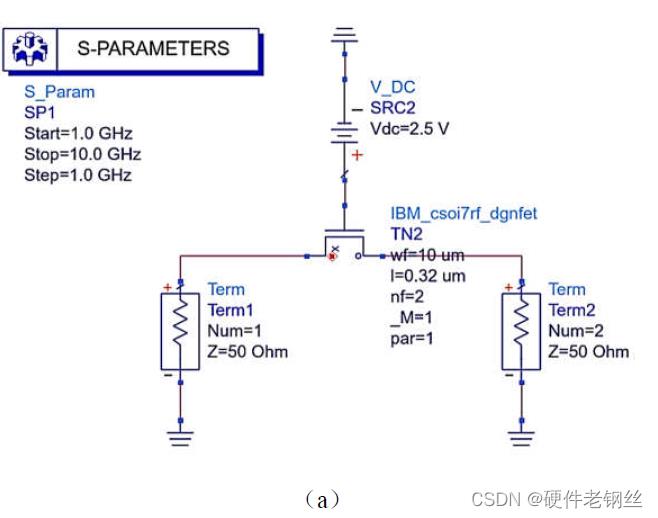
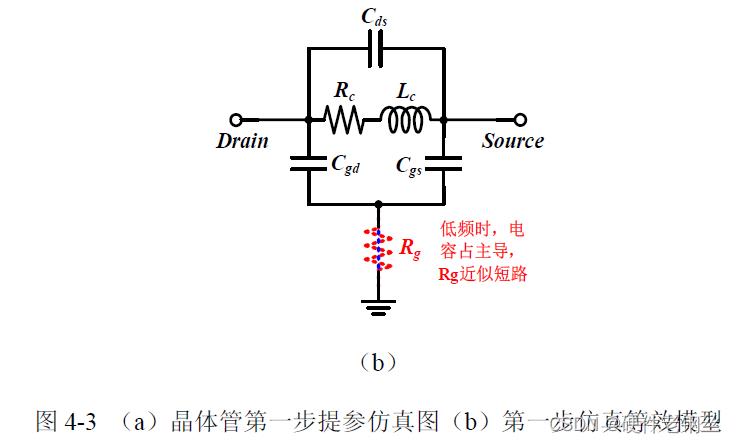
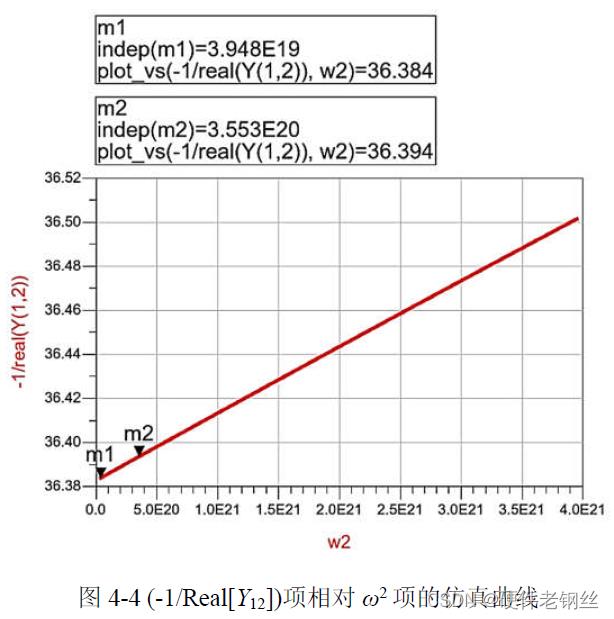
  低频时，因为模型并联支路电容占主导，栅极电阻近似短路，所以由图4-3（b）网络可以写出式（4-1），得出-1/Real[Y12]项与ω2 项成线性关系，斜率为Lc2/Rc，截距为Rc。通过仿真晶体管参数-1/Real[Y12]相对于ω2 的曲线（见图4-4），选取低频时的两个数据点m1 与m2，由式（4-2）计算曲线斜率a1，式（4-3）计算曲线截距b1 得Rc = b1 = 36.383 Ω，将Rc 值代入式（4-4）可得Lc = 33.43 pH。


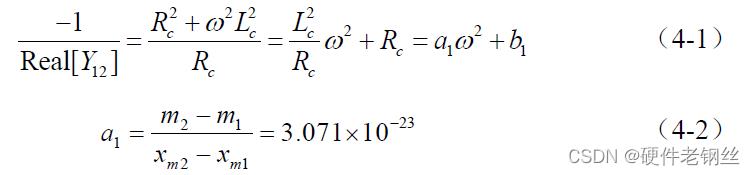
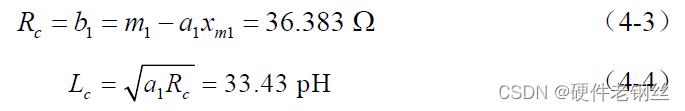
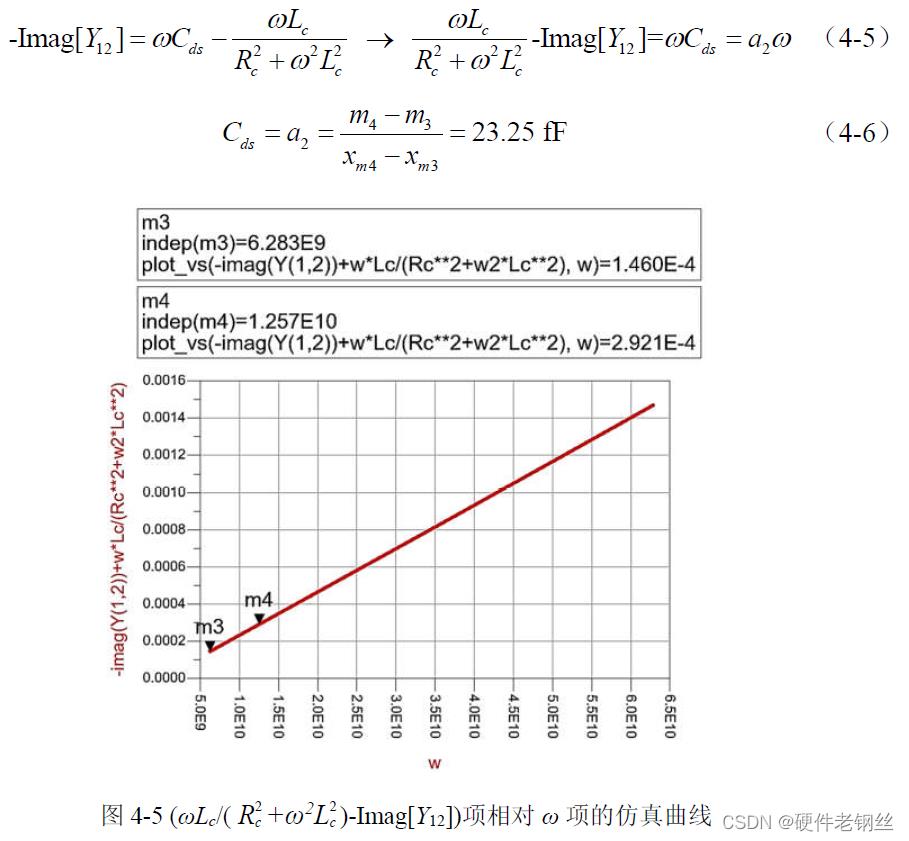
  电容Cds 的提取方法可以根据式（4-5），代入已提取的Rc 值与Lc 值仿真晶体管参数(4-5)相对于ω 的曲线（如图4-5 所示），在低频时从曲线中选取两个数据点m3 与m4，由式（4-6）计算曲线斜率a2，得Cds = 23.25 fF。

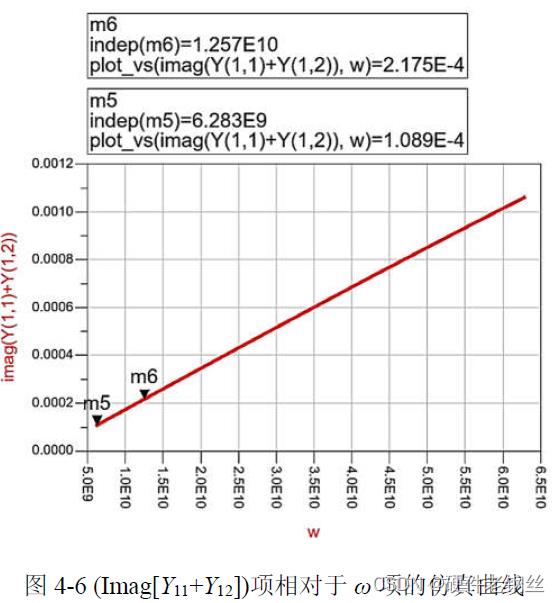
  Cgd 的参数提取方法如式（4-7）所示，通过仿真项Imag[Y11+Y12]相对于ω 的曲线（见图（4-6）），在低频时选取曲线的两个点m5 与m6，根据式（4-8）可得Cgd = 17.3 fF，又漏极与源极电压同为0V，晶体管为对称结构，因此Cgs = Cgd =17.3 fF

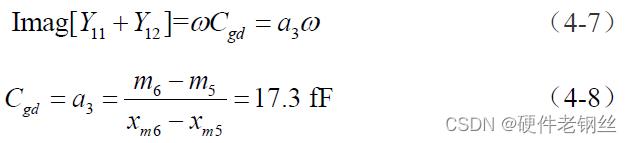
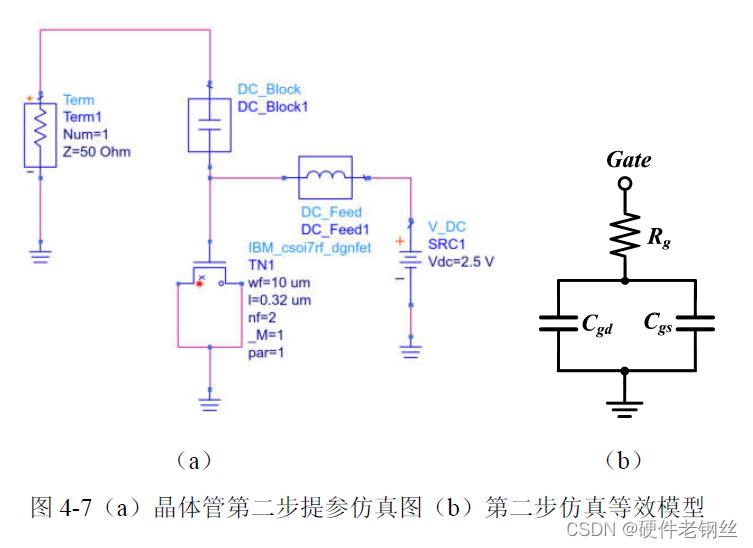
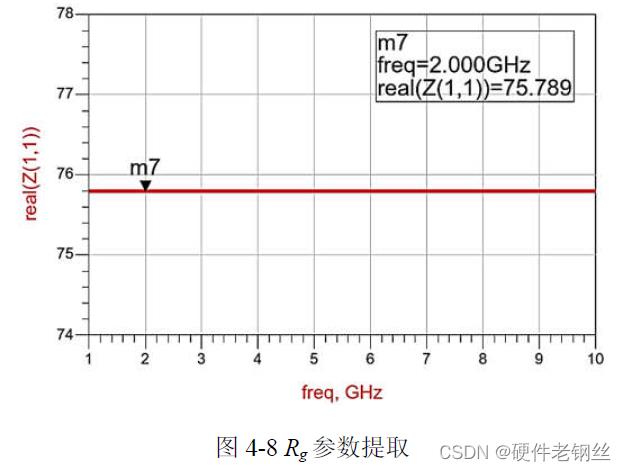
  以上为第一步仿真得到的寄生参数元件值，而提取栅极电阻Rg 则需要进行第二步仿真，仿真图如图4-7（a）所示，小信号模型见图4-7（b）。对该电路的晶体管Z 参数进行仿真取实部即可得到Rg，仿真结果见图4-8，Rg = 75.789 Ω。


  至此，晶体管工作在导通状态的所有寄生元件提取完毕。

2 晶体管关闭等效模型

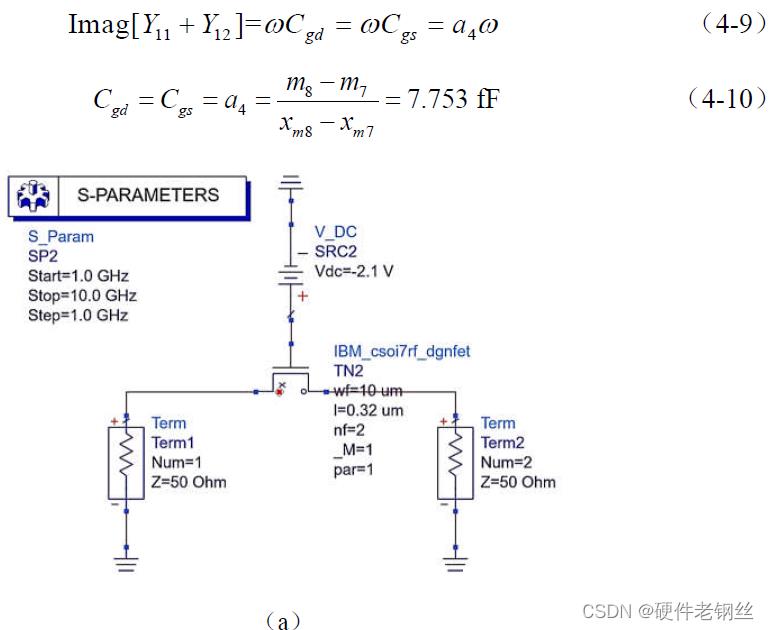
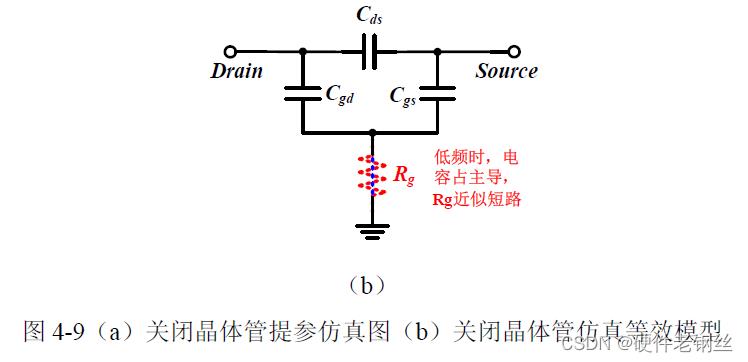
  由于栅极电阻值不会因电压偏置改变而改变，可以沿用节4.1 计算的Rg 值，因此晶体管关闭模型仅需一步仿真即可提取所有寄生参数。参数提取仿真图如图4-9（a）所示，开关选取的控制电压为-2.1 V，兼顾了实际负压提供条件。等效小信号模型见图4-9（b），与导通模型不同的是晶体管沟道尚未形成，导通电阻Rc 近似无穷大，寄生电容占主导作用。由关闭晶体管等效模型图，可以写出式（4-9），并作曲线图（4-10），由式（4-10）得电容Cgd = Cgs = 7.753 fF（模型对称）。



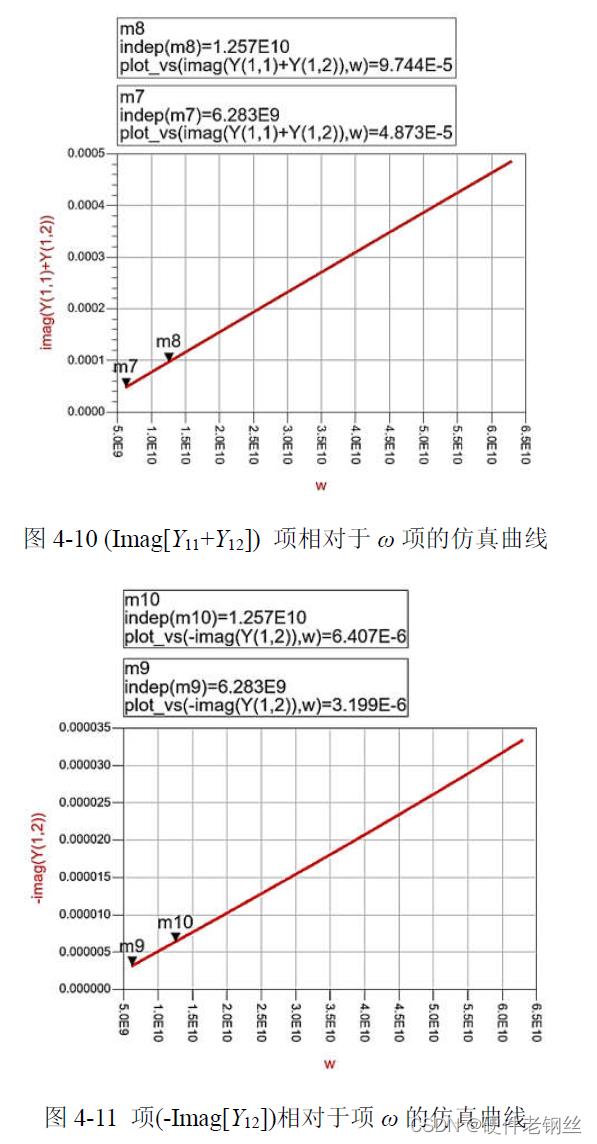
  晶体管关闭状态的电容Cds 由式（4-11）进行提取，作曲线图4-11，根据公式（4-12）得Cds = 0.51 fF。

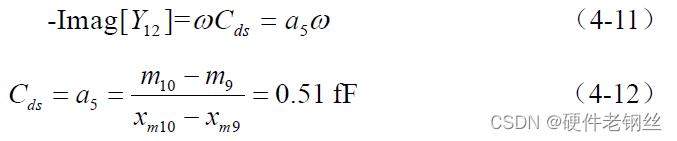
  至此，晶体管工作在关闭状态的所有寄生元件提取完毕。

3 等效模型仿真验证

  为验证晶体管导通与关闭状态等效模型的准确性，将其与PDK 模型仿真结果做对比，导通状态晶体管仿真电路图见4-3（a），模型仿真对比结果如图4-12 所示，因为开关晶体管模型是对称互易网络，有S11 = S22，S12 = S21，所以图中仅对比参数S11 与S12 的幅度与相位，可以看出导通等效模型与PDK 提供的模型在10 GHz内能很好地吻合。

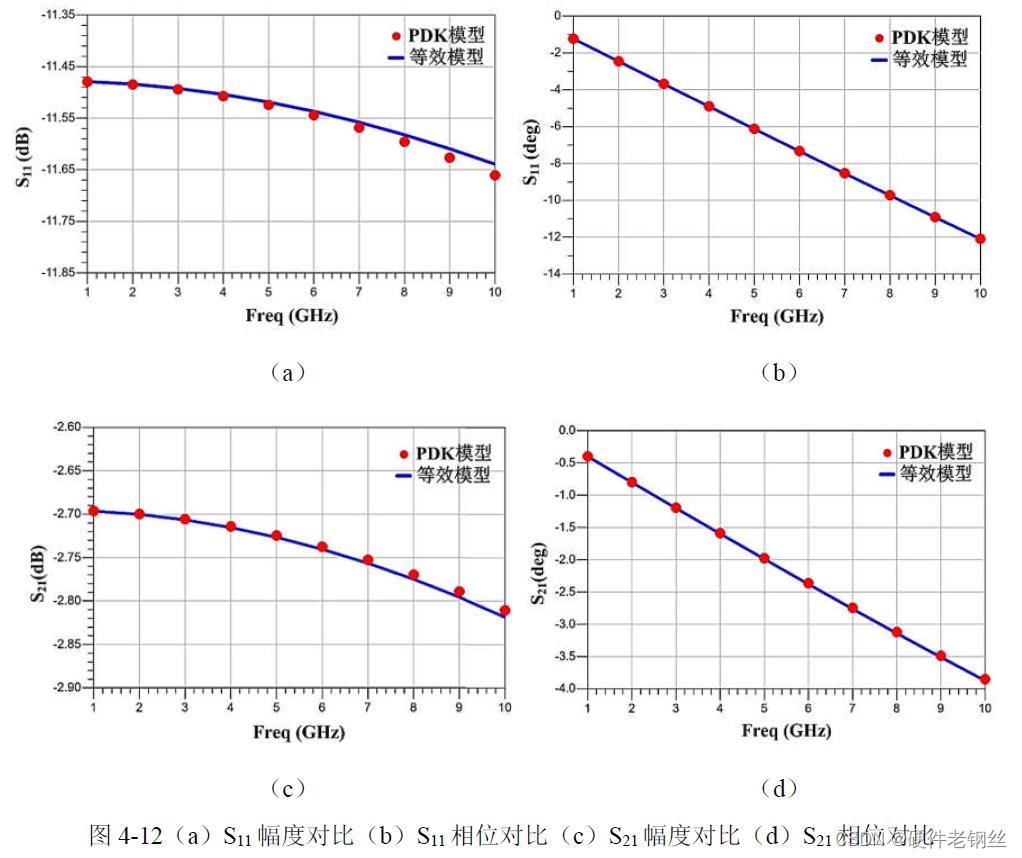
  关闭状态晶体管仿真电路图如图4-9（a）所示，等效模型仿真对比结果见图4-13，可知关闭状态的等效模型与PDK 模型同样在10 GHz 范围内较好地吻合。

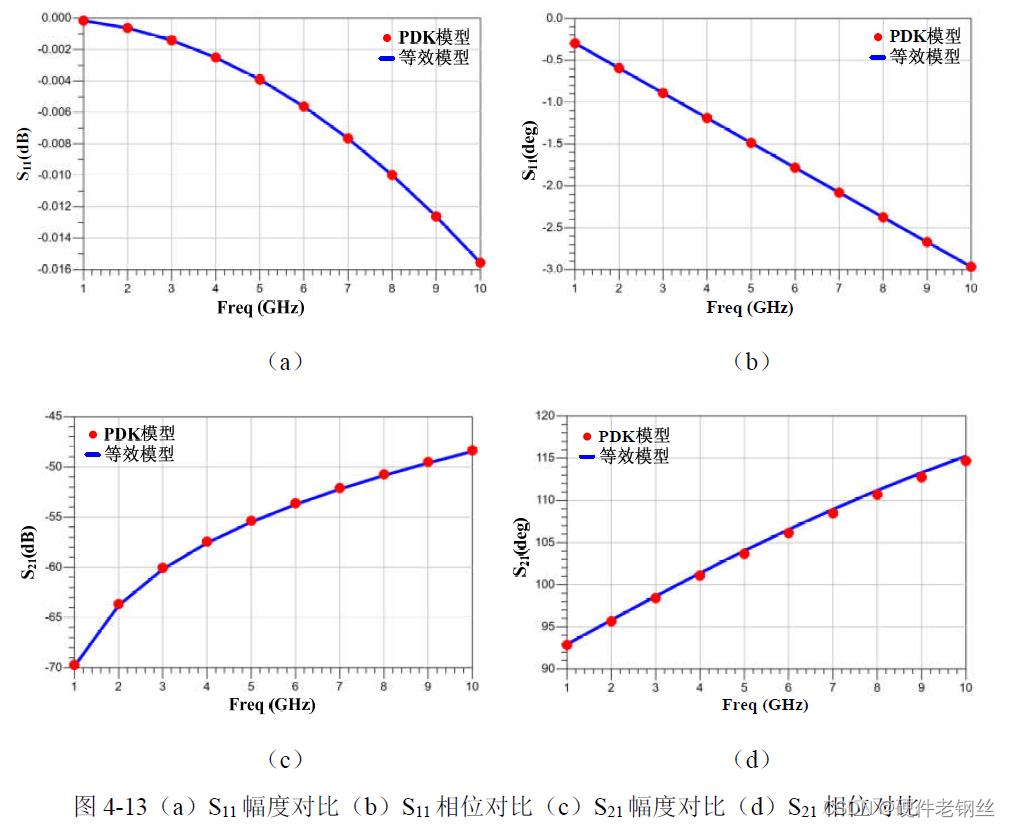
综上对比，可知开关晶体管导通与关闭等效模型在10 GHz 范围内能与PDK模型相匹配，不仅验证了等效模型的准确性，同时也验证了参数提取的正确性。说明等效模型具备电路设计的参考价值。

4 开关晶体管的品质因数

  开关晶体管的品质因数由Coff 与Ron 计算得到，公式为

  其中Ron 为晶体管的导通电阻，也即节4.1 提取的晶体管Rc 值。Coff 为晶体管关闭时的漏源总电容，又因为开关晶体管的栅极交流开路（栅极接高阻抗防止交流泄漏），Coff 可以由节4.2 提取的寄生电容计算，公式为

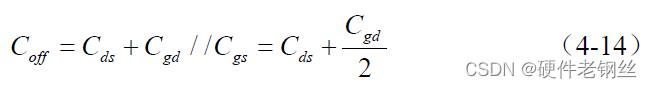
  根据式（4-13）（4-14）以及节4.1 与节4.2 的晶体管提取参数结果，可得本文选取工艺的开关晶体管品质因数为FOM = 36.383×4.39 = 160 fs。 品质因数是一个表征不同工艺开关性能的量，它的值越低，开关的插入损耗越低（Ron 越小），隔离度越高（Coff 越小）。

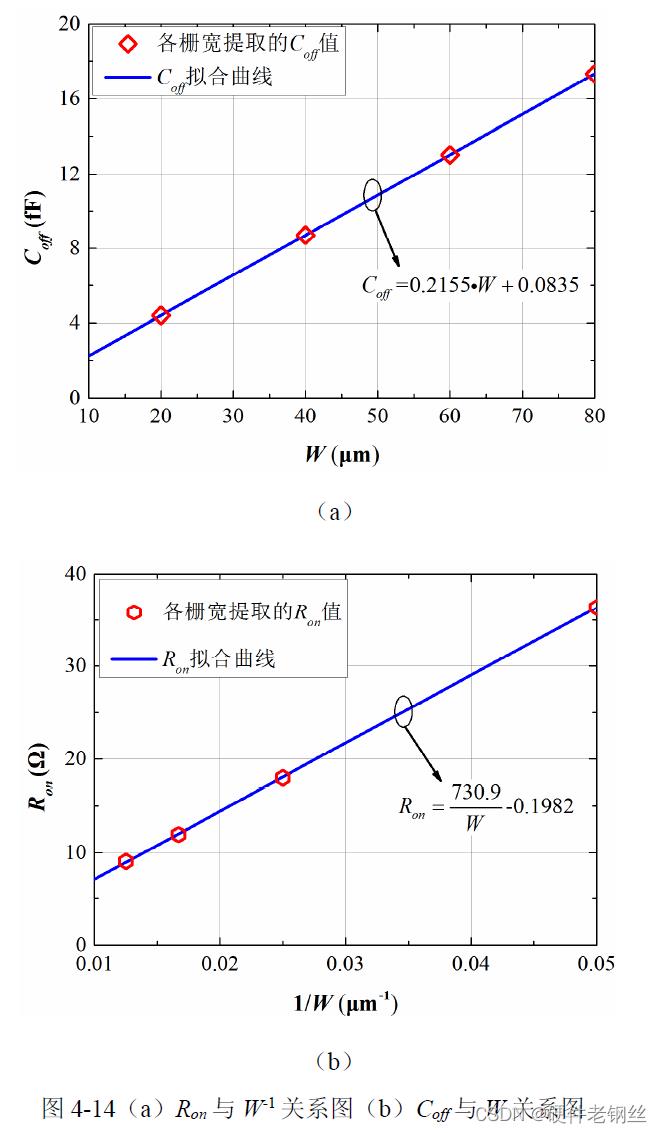
  为验证晶体管的品质因数与栅宽的关系，选取一组不同宽度的厚栅管仿真，晶体管尺寸为单指栅宽Wf = 10 μm，栅长L= 0.32 μm，栅指数分别为nf = 2、4、6、8，依据节4.1 与节4.2 的参数提取方法，提取相应晶体管的Ron 与Coff 的值，最终作图4-14。从图4-14（a）（b）中可以看出导通电阻与栅指数（也即栅宽）近似成反比例关系，关闭电容与栅指数（栅宽）近似成正比例关系，用matlab 软件作拟合曲线Ron vs W-1 与Coff vs W，W（μm）为晶体管总栅宽，得拟合曲线（4-15）（4-16）。两式的乘积约为常量157.5 fs，接近之前计算的160 fs，说明了开关晶体管的品质因数不由器件尺寸决定，它反应的是工艺整体的开关性能。