基于能量检测的调制方式识别算法MATLAB仿真,识别不同SNR下的MFSK和MPSK
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于能量检测的调制方式识别算法MATLAB仿真,识别不同SNR下的MFSK和MPSK相关的知识,希望对你有一定的参考价值。
UP目录
一、理论基础
随着无线通信的快速发展,用户对通信质量的要求越来越高,同时无线设备的大幅度增长,使得频谱资源显得更加重要。认知无线电(Cognitive Radio, CR)技术被当作解决频谱资源紧张、提高频谱利用率的强有力的技术,是下一代通信技术的重要组成成分。频谱感知是认知无线电技术实现的关键技术,通过频谱感知技术来感知信道中的频谱空洞,使得认知用户可以利用频谱空洞进行信息的传输,从而缓解了频谱资源紧张与通信业务需求之间的矛盾。调制样式自动识别系统包括以下几个部分:
信号预处理模块、特征提取模块和调制样式识别模块。
信号预处理模块的主要功能是为后续处理提供合适的数据,其任务一般包括:A/D转换、频率下变频、同相和正交分量分解、载频估计和载频分量的消除等。
特征提取模块是从输入的信号序列中提取对调制识别有用的信息,主要是从数据中提取信号的时域特征或变换域特征。时域特征包括信号的瞬时幅度、瞬时相位或瞬时频率的直方图或其它统计参数。变换域特征包括功率谱、谱相关函数、时频分布及其它统计参数。对于变换域特征,采用FFT方法就能很好的获取,而幅度、相位和频率等时域特征主要由Hi1bert变换法,同相正交(I—Q)分量法和过零检测法等获得。
调制样式识别的方法主要分为基于特征提取的统计模式识别和基于决策理论的最大似然假设检验,不论是决策论途径还是模式识别途径, 通信信号的自动调制识别实际上都是假设检验和统计推断这两个基本数学方法现。其中后者的两个步骤包括:一、对信号进行特征统计处理, 即构造信号的特征统计量; 二、根据某种准则, 将求得的信号特征量与门限进行比较, 并对其调制种类做出判决。
统计模式识别方法首先要从接收的信号中提取出特征参数,然后通过模式识别系统来确定信号调制类型。①基于统计参数的特征提取方法;②基于谱相关分析的特征提取方法;③基于时频分析的特征提取方法;④基于高阶统计量的特征提取方法;⑤基于信号星座图的特征提取方法。
决策论方法采用概率论和假设检验中的贝叶斯理论解决信号的识别问题,它根据信号的统计持性,通过理论分析与推导,得到检验统计量,然后与一个合适的门限进行比较,进行判定。
首先介绍了MPSK和MFSK两种类型的多进制调制方式,然后介绍了超短波信道的基本特点,主要包括误码率高、衰落、长传输距离、多径时延、多普勒频移。最后介绍了Longley-Rice模型、Okumura模型、CCIR模型、Egli模型和Hata模型等多种超短波信道模型。在超短波信道中,采用多种不同的调制方式,可以有效减少传输过程中所存在的噪声干扰,并增加通信距离。
针对不同调制方式的超短波信号的检测问题,本文首先介绍了传统的能量检测算法、匹配滤波检测算法、循环平稳检测算法,并通过MATLAB对三种检测算法进行了性能的分析,结合这些算法的优缺点,提出了一种融合多分辨功率谱和多分辨时频谱图的信号检测算法,通过MATLAB仿真分析其检测率-误警率性能指标。

表2的数据结论为信噪比分别在-15dB,-10dB,-5dB,-0dB, 5dB,10dB, 15dB,20dB,25dB,30dB以及无噪声下MPSK和MFSK两种调制方式所对应的功率谱峰值宽度值。
表2MPSK和MFSK功率谱峰值宽度值

从表2的仿真结果可知,对于不同的信噪比,MPSK调制方式的功率谱峰值宽度较大,其值均在200以上,MFSK调制方式的功率谱峰值宽度较小,其值均在100以下,根据这个特性,可以有效区分MPSK和MFSK两种调制方式。特别的,当信噪比SNR为-5dB的时候,通过这个方法也可以有效区分MPSK和MFSK两种调制方式。但是当噪声干扰较大的时候,即信噪比小于-10dB的时候,2FSK的功率谱峰值宽度大于200,而其余情况,MFSK的功率谱峰值宽度均在100附近或者小于100。
二、核心程序
...........................................................
SNR0 = -20;
N0 = 1000;
y_2FSK = zeros(1,N0);
y_4FSK = zeros(1,N0);
y_8FSK = zeros(1,N0);
y_2PSK = zeros(1,N0);
y_4PSK = zeros(1,N0);
y_8PSK = zeros(1,N0);
%2FSK
y_2FSK = func_2FSK(N0);
%4FSK
y_4FSK = func_4FSK(N0);
%8FSK
y_8FSK = func_8FSK(N0);
%BPSK
y_2PSK = func_2PSK(N0);
%QPSK
y_4PSK = func_4PSK(N0);
%8PSK
y_8PSK = func_8PSK(N0);
%调制识别
y_2FSKn = func_add_noise(y_2FSK,SNR0);
y_4FSKn = func_add_noise(y_4FSK,SNR0);
y_8FSKn = func_add_noise(y_8FSK,SNR0);
y_2PSKn = func_add_noise(y_2PSK,SNR0);
y_4PSKn = func_add_noise(y_4PSK,SNR0);
y_8PSKn = func_add_noise(y_8PSK,SNR0);
L=N0; %信号样本
t = (0:L-1)*1/fs; %时间序列(时间轴)
y = y_8PSKn; %混入噪声信号 randn(size(t))生成与数组t大小相同的随机数组
figure(1)
subplot(211);
plot(t,y)
xlabel('times');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%进行能量检测
NFFT = 2^nextpow2(L); %找出大于等于L且最接近L的2的整数次幂长度, 如L=10 NFFT=16
Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值)
f = fs/2*linspace(0,1,NFFT/2); %频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的)
subplot(212);
plot(f,sqrt(2)*abs(Y(1:NFFT/2))/2) % 画出频率幅度图形,可以看出120Hz
xlabel('Frequency');
up63三、测试结果
通过matlab2021a仿真结果如下:
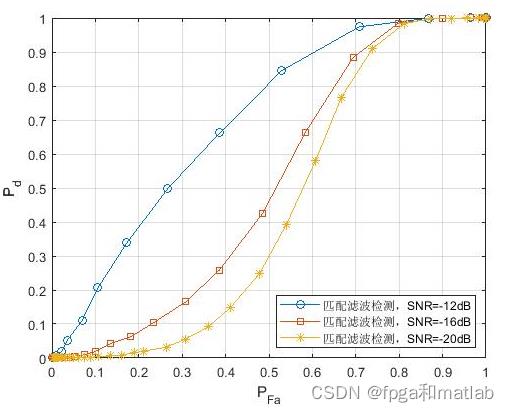
以上是关于基于能量检测的调制方式识别算法MATLAB仿真,识别不同SNR下的MFSK和MPSK的主要内容,如果未能解决你的问题,请参考以下文章