在LaTeX中调用Mathematica代码求解绘图（WolframLanguage）

Posted 2023-01-24 Z.Q.Feng

文章目录

• 一、前言
• 二、下载功能补足文件
• 三、使用功能补足文件
• 三、LaTeX命令调用
• 四、常用的LaTeX-alpha2命令
• • 1. 直接运行MMA命令
  • 2. 调用MMA绘制图像
  • 3. 调用MMA求解微分方程
• 五、总结

---

一、前言

在 LaTeX 中使用 Mathematica 代码，一种方式是将 Mathematica 代码的输出转化为 LaTeX 格式，然后复制粘贴，最近发现了一个不错的项目，能够直接在 LaTeX 代码中插入 Mathematica 代码进行求解与绘图，项目地址如下：https://github.com/stevenliuyi/latex-alpha2

LaTeX-alpha2 项目是 LaTeX-alpha 项目的升级，LaTeX-alpha 项目距今已经太古老啦。

---

二、下载功能补足文件

我们直接采用 Git 工具即可：

cd ~/Downloads
git clone https://github.com/stevenliuyi/latex-alpha2.git

接着进入目录，我们可以看到对应的 .sty 文件：

---

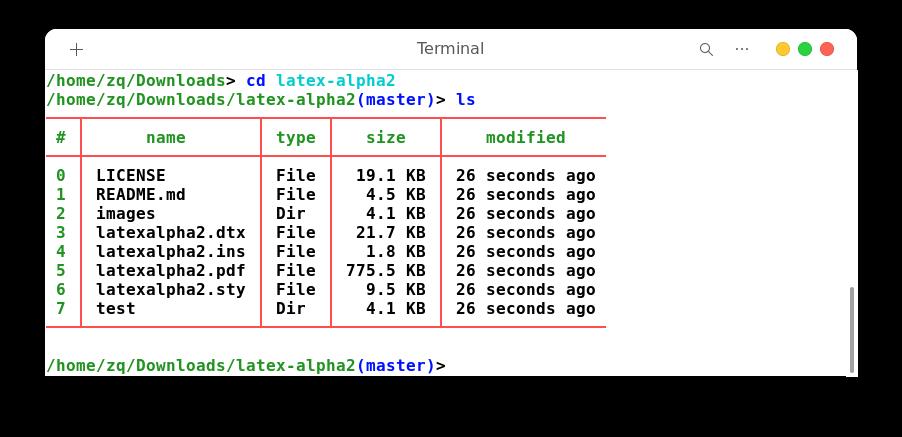
三、使用功能补足文件

有两种方法：

• 一是将 latexalpha2.sty 文件移动到我们的 LaTeX 文件所在的文件目录下，这样每编辑一个 LaTeX 文件我们都要进行对应的复制移动

• 二是直接将 latexalpha2.sty 文件移动到 TEXMF 目录下，在我的电脑上它的路径是：/usr/local/texlive/2021/texmf-dist/tex/latex，可以使用 texhash 命令查看自己电脑上的这个路径，新建一个 latexalpha2 目录：

  cd /usr/local/texlive/2021/texmf-dist/tex/latex
  sudo mkdir latexalpha2
  

  接着移动 latexalpha2.sty 文件到上述目录：

  sudo cp ~/Downloads/latex-alpha2/latexalpha2.sty ./latexalpha2
  

  刷新 LaTeX 的包数据库：

  sudo texhash
  

---

三、LaTeX命令调用

添加包的调用：

\\usepackagelatexalpha2

LaTeX 中使用 latexalpha2 必须以 -shell-escape 参数调用编译，所以需要我们修改编译参数，打开 TexStudio，设置如下：

Options $\to$ Configure TexStudio… $\to$ Commands

这里我的编译器选择的是 XeLaTeX，所以在 XeLaTeX 编译命令后加上参数 -shell-escape，大致设置如下：

---

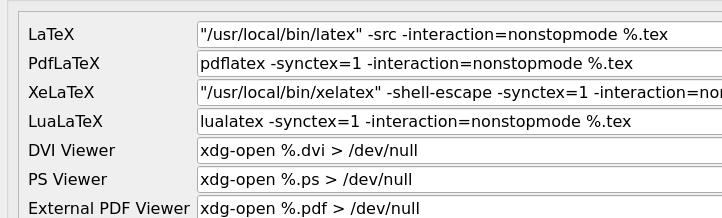
四、常用的LaTeX-alpha2命令

1. 直接运行MMA命令

调用格式如下：

$\\wolframMMA命令$

例如直接在 LaTeX 中计算函数 $f(x)=\frac{1}{\sqrt{1-x^2}}$ 的二阶导数：

$\\wolframD[1/(1-x^2)^(1/2), x, 2]$

输出如下：

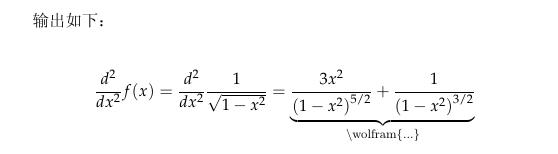
注：这里的计算建议不要放在行内公式环境 ($...$) 内，可另起一行或使用行间公式环境($$...$$)

2. 调用MMA绘制图像

命令如下：

\\wolframgraphics[文件格式]MMA命令文件名

例如绘制函数 $f(x,y)=sin(x)cos(y)$在$[-2\pi ,2\pi ]$ 上的 3 维函数图像：

\\beginfigure[h] 
	\\centering
	\\wolframgraphics[pdf]Plot3D[Sin[x]Cos[y], x, -2Pi, 2Pi, y, -2Pi, 2Pi]example
	\\includegraphics[width=14cm]example.pdf
	\\captionPlot3D of $f(x,y)=\\sin(x)\\cos(y)$
\\endfigure

输出如下所示：

再比如绘制 $tan(x)$ 在 $[0,2\pi ]$ 上的图像：

\\beginfigure[!htbp] 
	\\centering
	\\wolframgraphics[pdf]Plot[Tan[x], x, 0, 2Pi]example1
	\\includegraphics[width=14cm]example1.pdf
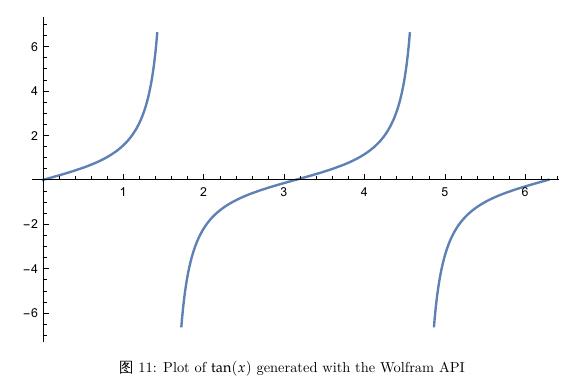
	\\captionPlot of $\\tan(x)$ generated with the Wolfram API
\\endfigure

输出如下所示：

3. 调用MMA求解微分方程

命令如下：

\\wolframdsolve线型微分方程待求解函数自变量

例如求解一阶线性微分方程 $\frac{d}{dx}y+y=asin(x)$ 的解：

\\wolframdsolvey'[x] + y[x] == a*Sin[x]y[x]x

输出如下：

---

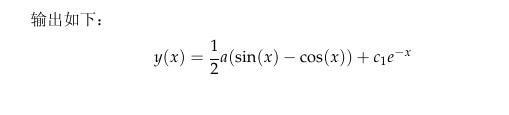
五、总结

LaTeX 的强大之处可能就在于它能够如此便捷的与其他语言相链接吧。