从固定管线到可编程管线:十段代码入门OpenGL
Posted 天元浪子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从固定管线到可编程管线:十段代码入门OpenGL相关的知识,希望对你有一定的参考价值。
文章目录
- 1. 最简单的OpenGL应用程序
- 2. 视点系统和投影矩阵
- 3. 深度缓冲区和深度测试
- 4. 模型的旋转和平移
- 5. VBO和顶点混合数组
- 6. 纹理映射和纹理坐标
- 7. 光照和法向量计算
- 8. 最简单的着色器程序
- 9. 着色器中的MVP矩阵
- 10. 着色器中的漫反射、镜面反射和高光计算
1. 最简单的OpenGL应用程序
有兴趣点进来阅读此文的同学,想必都已经安装了PyOpenGL,如果没有,请运行pip install pyopengl命令立即安装。使用windows的同学,也可以照此安装,不过可能会遇到因为freeglut.dll缺失或版本错误导致的glutInit函数不可用问题。点击“Python模块仓库”下载适合自己的版本,直接安装.whl文件,也许是windows平台上更稳妥的选择。
demo_01.py
#!/usr/bin/env python3
"""最简单的OpenGL应用程序"""
from OpenGL.GL import * # 导入核心库GL,该库所有函数均以gl为前缀
from OpenGL.GLUT import * # 导入工具库GLUT,该库所有函数均以glut为前缀
def draw():
"""绘制模型"""
glClear(GL_COLOR_BUFFER_BIT) # 清除缓冲区
glBegin(GL_TRIANGLES) # 开始绘制三角形
glColor(1.0, 0.0, 0.0) # 设置当前颜色为红色
glVertex(0.0, 1.0, 0.0) # 设置第1个顶点
glColor(0.0, 1.0, 0.0) # 设置当前颜色为绿色
glVertex(-1.0, -1.0, 0.0) # 设置第2个顶点
glColor(0.0, 0.0, 1.0) # 设置当前颜色为蓝色
glVertex(1.0, -1.0, 0.0) # 设置第3个顶点
glEnd() # 结束绘制三角形
glFlush() # 输出缓冲区
if __name__ == "__main__":
glutInit() # 1. 初始化glut库
glutCreateWindow('OpenGL Demo') # 2. 创建glut窗口
glutDisplayFunc(draw) # 3. 绑定模型绘制函数
glutMainLoop() # 4. 进入glut主循环
这段代码使用OpenGL的GLUT库构建了一个最简单的OpenGL应用程序——绘制三角形,运行界面截图如下。
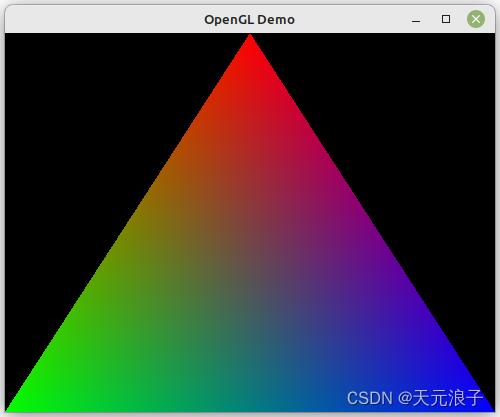
代码前两行导入GL库和GLUT库——前者是OpenGL的核心库,实现绘图功能,后者是不依赖于窗口平台的OpenGL工具库,用于构建窗口程序。尽管OpenGL包含了多个库,最常用的其实只有三个库,除了这段代码用到了GL和GLUT,还有一个实用库GLU,接下来就会用到。每个OpenGL库都有大量的函数,但库和函数命名规则非常合理,每个函数都以小写的库名作为前缀,代码读起来一目了然,非常清晰。
使用GLUT创建OpenGL应用程序非常简单,就像代码中展示的那样,只需要四步——当然,前提是先准备好绘图函数,也就是上面代码中的draw函数。
这段代码中的draw函数演示了线段的绘制流程。OpenGL可以绘制点、线、面等十种基本图元,每种图元的顶点、颜色以及法向量、纹理坐标等,都必须包含在glBegin函数和glEnd函数之间,而glBegin函数的参数就是十种基本图元之一。
OpenGL基本图元速查表
| 参数 | 说明 |
|---|---|
| GL_POINTS | 绘制一个或多个顶点,顶点之间是相互独立的 |
| GL_LINES | 绘制线段,每两个顶点对应一条单独的线段。若顶点数为奇数,则忽略最后一个 |
| GL_LINE_STRIP | 绘制连续线段,各个顶点依次顺序连接 |
| GL_LINE_LOOP | 绘制闭合的线段,各个顶点依次顺序连接,最后首尾相接 |
| GL_POLYGON | 绘制凸多边形,多边形的边缘决不能相交 |
| GL_TRIANGLES | 绘制一个或多个三角形,每三个顶点对应一个三角形。若顶点个数不是三的倍数,则忽略多余的顶点 |
| GL_TRIANGLE_STRIP | 绘制连续三角形,每个顶点与其前面的两个顶点构成下一个三角形 |
| GL_TRIANGLE_FAN | 绘制多个三角形组成的扇形,每个顶点与其前面的顶点和第一个顶点构成下一个三角形 |
| GL_QUADS | 绘制一个或多个四边形,每四个顶点对应一个四角形。若顶点个数不是四的倍数,则忽略多余的顶点 |
| GL_QUAD_STRIP | 绘制连续四边形,每一对顶点与其前面的一对顶点构成下一个四角形 |
借助于图形,更容易理解基本图元的差异和用法。懒得画图了,在网上随便找了一张,顶点顺序也许和读者的习惯并不一致,但在逻辑上是没有问题的。

举个例子:在glBegin函数和glEnd函数之间有6个顶点,序号分别是0~5。如果绘制独立三角面(GL_TRIANGLES),则顶点(0, 1, 2)构成一个三角形,顶点(3, 4, 5)构成一个三角形,总共2个三角形;如果绘制带状三角面(GL_TRIANGLE_STRIP),则有4个三角形,分别是顶点(0, 1, 2)、顶点(2, 1, 3)、顶点(2, 3, 4)和顶点(4, 3, 5);如果绘制扇面(GL_TRIANGLE_FAN),同样有4个三角形,分别是顶点(0, 1, 2)、顶点(0, 2, 3)、顶点(0, 3, 4)和顶点(0, 4, 5)。
绘制三角形、四边形、多边形时,顶点的顺序决定了哪个面是图元的正面——正反面的意义不仅仅是确定法向量的方向,还为固定管线中的面裁剪和可编程管线中的弃用片元提供了依据。在OpenGL系统中默认逆时针顺序构建的面是正面,使用glFrontFace函数可以重新设置。
2. 视点系统和投影矩阵
运行第一段代码,改变窗口大小及宽高比,仔细观察就会发现三角形的宽高比例会随窗口宽高比例变化而变化,但是 x x x 轴和 y y y 轴的显示区间始终都是(-1, 1), x x x 轴从屏幕的左侧指向右侧, y y y 轴从屏幕的底部指向上方, z z z 轴垂直于屏幕。OpenGL使用右手系坐标,参考下图,不难想象出 z z z 轴的方向是从屏幕里面指向外面的。
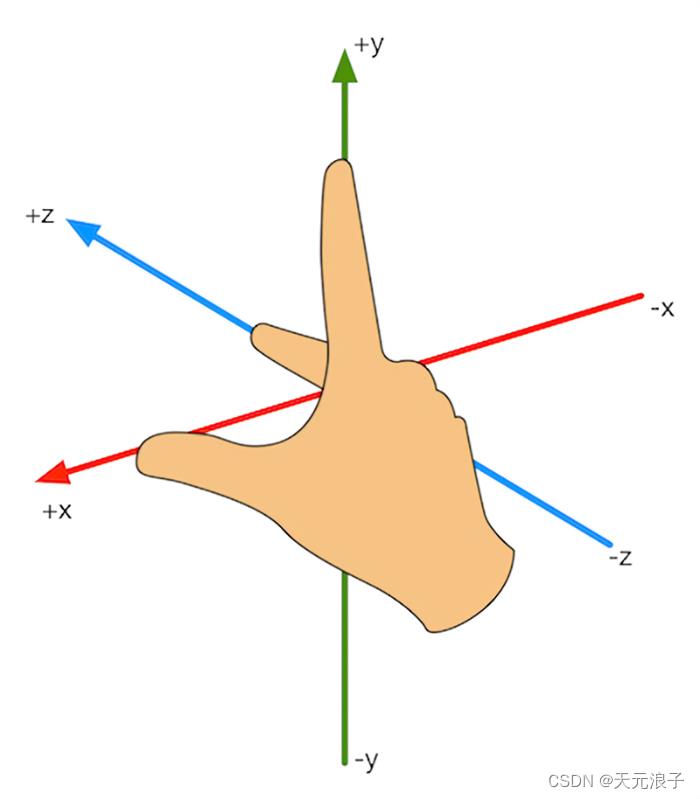
接下来有一个问题需要思考:如何看到第一段代码展示的三角形的背面呢?无论怎样调整眼睛和屏幕的相对关系,看到的始终是平面的2D效果。设想一下,把有深度的屏幕(默认 z z z 轴就是深度轴)视为一个舞台场景,将一架相机放入场景中,改变相机的位置和拍摄角度,不就可以看到想要的效果了吗?
那么,如何定义场景中的这一架相机呢?现实生活中使用相机拍照,大致有以下三个要素。
- 相机位置:决定了相机和拍摄目标之间的空间相对关系
- 拍摄角度:相机的姿态,包括横置、竖置、平视、俯视、仰视等
- 镜头焦距:决定视野宽窄,焦距越小,视野越宽
在3D场景中的相机与之类似,只不过是用相机和拍摄目标之间的距离、相机的方位角和高度角替代了相机位置和拍摄角度,三要素变成了四要素。
- 相机和拍摄目标之间的距离(代码中简写为dist)
- 方位角(代码中简写为azim)
- 高度角(代码中简写为elev)
- 水平视野角度(代码中简写为fovy)
在一个OpenGL空间直角坐标系中,点 a a a 为 z z z 轴正半轴上一点,假设相机位置在空间点 p p p 处,点 b b b 为点 p p p 在 x o z xoz xoz 平面上的投影,那么线段 o p op op 的长度就是相机和坐标原点之间的距离dist, ∠ a o b ∠aob ∠aob 即为方位角azim, ∠ p o b ∠pob ∠pob 即为高度角elev。相机绕 y y y 轴逆时针旋转时,方位角正向增加;相机向 y y y 轴正方向升高时,高度角正向增加。

至此,一个完整的视点系统就建立起来了。视点系统对应着一个矩阵,相机方位角、高度角以及距离的变化就是改变这个矩阵,这个矩阵叫做视点矩阵(View Matrix)。视点矩阵是玩转OpenGL必须要理解的三个矩阵之一,另外两个是投影矩阵(Projection Matrix)和模型矩阵(Model Matrix),三个矩阵合称MVP矩阵。喜欢篮球或足球的话,很容易记住这个组合——MVP,最有价值球员。
demo_02.py
#!/usr/bin/env python3
"""视点系统和投影矩阵"""
import numpy as np
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
dist = 5.0 # 全局变量:相机与坐标原点之间的距离
azim = 0.0 # 全局变量:方位角
elev = 0.0 # 全局变量:高度角
fovy = 40.0 # 全局变量:水平视野角度
near = 2.0 # 全局变量:最近对焦距离
far = 1000.0 # 全局变量:最远对焦距离
cam = (0.0, 0.0, 5.0) # 全局变量:相机位置
csize = (800, 600) # 全局变量:窗口大小
aspect = csize[0]/csize[1] # 全局变量:窗口宽高比
mouse_pos = None # 全局变量:鼠标位置
def click(btn, state, x, y):
"""鼠标按键和滚轮事件函数"""
global mouse_pos
if (btn == 0 or btn == 2) and state == 0: # 左键或右键被按下
mouse_pos = (x, y) # 记录鼠标位置
glutPostRedisplay() # 更新显示
def drag(x, y):
"""鼠标拖拽事件函数"""
global mouse_pos, azim, elev, cam
dx, dy = x-mouse_pos[0], y-mouse_pos[1] # 计算鼠标拖拽距离
mouse_pos = (x, y) # 更新鼠标位置
azim = azim - 180*dx/csize[0] # 计算方位角
elev = elev + 90*dy/csize[1] # 计算高度角
d = dist * np.cos(np.radians(elev))
x_cam = d*np.sin(np.radians(azim))
y_cam = dist*np.sin(np.radians(elev))
z_cam = d*np.cos(np.radians(azim))
cam = [x_cam, y_cam, z_cam] # 更新相机位置
glutPostRedisplay() # 更新显示
def reshape(w, h):
"""改变窗口大小事件函数"""
global csize, aspect
csize = (w, h) # 保存窗口大小
aspect = w/h if h > 0 else 1e4 # 更新窗口宽高比
glViewport(0, 0, w, h) # 设置视口
glutPostRedisplay() # 更新显示
def draw():
"""绘制模型"""
glClear(GL_COLOR_BUFFER_BIT) # 清除缓冲区
glMatrixMode(GL_PROJECTION) # 操作投影矩阵
glLoadIdentity() # 将投影矩阵设置为单位矩阵
gluPerspective(fovy, aspect, near, far) # 生成透视投影矩阵
gluLookAt(*cam, *[0,0,0], *[0,1,0]) # 设置视点矩阵
glBegin(GL_TRIANGLES) # 开始绘制三角形
glColor(1.0, 0.0, 0.0) # 设置当前颜色为红色
glVertex(0.0, 1.0, 0.0) # 设置顶点
glColor(0.0, 1.0, 0.0) # 设置当前颜色为绿色
glVertex(-1.0, -1.0, 0.0) # 设置顶点
glColor(0.0, 0.0, 1.0) # 设置当前颜色为蓝色
glVertex(1.0, -1.0, 0.0) # 设置顶点
glEnd() # 结束绘制三角形
glBegin(GL_LINES) # 开始绘制线段
glColor(1.0, 0.0, 1.0) # 设置当前颜色为紫色
glVertex(0.0, 0.0, -1.0) # 设置线段顶点(z轴负方向)
glColor(0.0, 0.0, 1.0) # 设置当前颜色为蓝色
glVertex(0.0, 0.0, 1.0) # 设置线段顶点(z轴正方向)
glEnd() # 结束绘制线段
glFlush() # 执行缓冲区指令
if __name__ == "__main__":
glutInit() # 1. 初始化glut库
glutInitWindowSize(*csize) # 2.1 设置窗口大小
glutCreateWindow('OpenGL Demo') # 2.2 创建glut窗口
glutDisplayFunc(draw) # 3.1 绑定模型绘制函数
glutReshapeFunc(reshape) # 3.2 绑定窗口大小改变事件函数
glutMouseFunc(click) # 3.3 绑定鼠标按键
glutMotionFunc(drag) # 3.4 绑定鼠标拖拽事件函数
glutMainLoop() # 4. 进入glut主循环
这段代码依旧是绘制了一个三角形,外加一条和 z z z 轴重合的线段。现在拖拽鼠标改变相机位置就能看到三角形的背面了,并且改变窗口大小时,三角形的宽高比例不再随着窗口的宽高比例的改变而改变。运行界面截图如下。
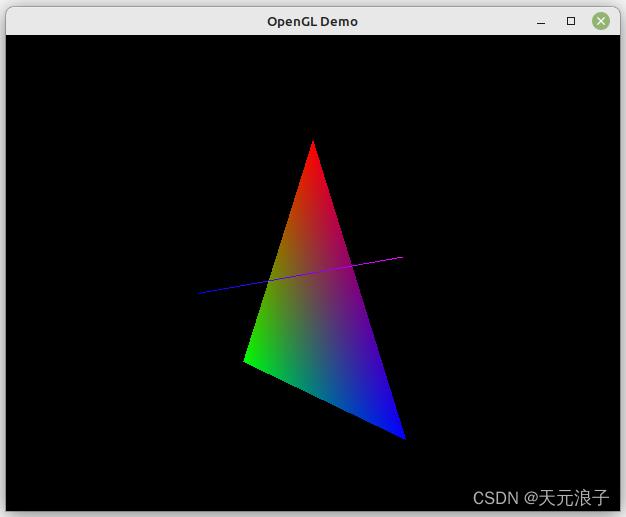
前面说过OpenGL有三个最常用的库,第一段代码用到了GL库和GLUT库,这段代码用到了了第三个库——GLU库中的两个函数,一个是gluPerspective,用来生成透视投影矩阵,一个是gluLookAt,用来设置视点矩阵。
生成投影矩阵需要4个参数,分别是fovy(相机水平视野角度)、aspect(窗口宽高比),以及near(最近对焦距离)和far(最远对焦距离)。near和far是相对于相机的距离,距离相机小于near或者大于far的目标都不会显示在场景中。
生成视点矩阵需要9个参数,分成3组,分别是相机位置、视点坐标系统原点和指向相机上方的单位向量。相机位置不言自明,视点坐标系统原点可以理解为相机的对焦点,代码中直接使用了坐标系原点,即相机的焦点始终对准坐标系原点。指向相机上方的单位向量说的是相机的姿态——是横置还是竖置抑或是旋转180°,这是暂时固定指向 y y y 轴正方向,后续代码会做相应处理。
3. 深度缓冲区和深度测试
在讲述视点矩阵和投影矩阵时,我有意回避了很多复杂的概念,目的是帮助初学者快速理解代码——有了代码,才能在实践中深入理解OpenGL中那些复杂的概念。不过,简化也带来了一些副作用,比如:
- 三角形无法遮住其背后的线段,没有实现深度遮挡
- 不能缩放视野,无法抵近观察三角形和线段
- 使用了很多全局变量,读着吃力,维护起来也很困难,难以实现代码复用
第1个问题中的深度遮挡,简单点说就是前面的模型遮挡后面的模型,复杂点说,对于半透明模型在渲染时还要考虑先后顺序。在3D绘图中实现深度遮挡,只需要开启深度测试并设置深度测试函数的参数就可以了。在此之前,需要先在GLUT的显示模式中启用深度缓冲区。这些工作看似繁琐,其实只需要3行代码。
那么,深度缓冲区究竟是什么?为什么要做深度测试呢?所谓深度缓冲区,就是一块内存区域,存储了屏幕上每个像素点对应的模型上的点和相机的距离,也就是深度值,值越大,离摄像机就越远。渲染像素化后的模型时,要对每个点做深度测试,判断一个点的深度和该点所对应的屏幕上的点的缓存深度谁前谁后,据此决定该点是否被遮挡。深度测试由深度测试函数实现,但需要用户提供测试规则。常用的测试规则见下表。为便于理解,这里我故意混淆了点和片元的概念,待了解了着色器之后,读者自会辨查。
OpenGL深度测试规则速查表
| 规则 | 说明 |
|---|---|
| GL_ALWAYS | 总是通过深度测试 |
| GL_NEVER | 总是不通过深度测试 |
| GL_LESS | 片元深度值小于缓冲的深度值时通过测试 |
| GL_EQUAL | 片元深度值等于缓冲区的深度值时通过测试 |
| GL_LEQUAL | 片元深度值小于等于缓冲区的深度值时通过测试 |
| GL_GREATER | 片元深度值大于缓冲区的深度值时通过测试 |
| GL_NOTEQUAL | 片元深度值不等于缓冲区的深度值时通过测试 |
| GL_GEQUAL | 片元深度值大于等于缓冲区的深度值时通过测试 |
第2个问题,关于缩放视野,可以用改变相机水平视野角度解决,就像拍照时使用变焦镜头拉近拉远一样,变焦就是改变了镜头的视野角度。如果相机没有变焦功能,那就只能走进或远离拍摄目标,也就是改变相机和拍摄目标之间的距离,同样可以缩放视野。
第3个问题,可以用面向对象编程(OOP)的方式解决。下面的代码基于GLUT库封装了一个3D场景类,启用了深度检测,封装了相机拖拽、视野缩放、相机姿态还原等鼠标操作,还支持自定义高度轴——建筑和空间领域更习惯用 z z z 轴作为高度轴。用户只要在派生类中重写draw函数,就可以方便地复用这段代码了。
demo_03.py
#!/usr/bin/env python3
"""深度缓冲区和深度测试"""
import numpy as np
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
class BaseScene:
"""基于OpenGl.GLUT的三维场景类"""
def __init__(self, **kwds):
"""构造函数"""
self.csize = kwds.get('size', (960, 640)) # 画布分辨率
self.bg = kwds.get('bg', [0.0, 0.0, 0.0]) # 背景色
self.haxis = kwds.get('haxis', 'y').lower() # 高度轴
self.oecs = kwds.get('oecs', [0.0, 0.0, 0.0]) # 视点坐标系ECS原点
self.near = kwds.get('near', 2.0) # 相机与视椎体前端面的距离
self.far = kwds.get('far', 1000.0) # 相机与视椎体后端面的距离
self.fovy = kwds.get('fovy', 40.0) # 相机水平视野角度
self.dist = kwds.get('dist', 5.0) # 相机与ECS原点的距离
self.azim = kwds.get('azim', 0.0) # 方位角
self.elev = kwds.get('elev', 0.0) # 高度角
self.aspect = self.csize[0]/self.csize[1] # 画布宽高比
self.cam = None # 相机位置
self.up = None # 指向相机上方的单位向量
self._update_cam_and_up() # 计算相机位置和指向相机上方的单位向量
self.left_down = False # 左键按下
self.mouse_pos = (0, 0) # 鼠标位置
# 保存相机初始姿态(视野、方位角、高度角和距离)
self.home = 'fovy':self.fovy, 'azim':self.azim, 'elev':self.elev, 'dist':self.dist
def _update_cam_and_up(self, oecs=None, dist=None, azim=None, elev=None):
"""根据当前ECS原点位置、距离、方位角、仰角等参数,重新计算相机位置和up向量"""
if not oecs is None:
self.oecs = [*oecs,]
if not dist is None:
self.dist = dist
if not azim is None:
self.azim = (azim+180)%360 - 180
if not elev is None:
self.elev = (elev+180)%360 - 180
up = 1.0 if -90 <= self.elev <= 90 else -1.0
azim, elev = np.radians(self.azim), np.radians(self.elev)
d = self.dist * np.cos(elev)
if self.haxis == 'z':
azim -= 0.5 * np.pi
self.cam = [d*np.cos(azim)+self.oecs[0], d*np.sin(azim)+self.oecs[1], self.dist*np.sin(elev)+self.oecs[2]]
self.up = [0.0, 0.0, up]
else:
self.cam = [d*np.sin(azim)+self.oecs[0], self.dist*np.sin(elev)+self.oecs[1], d*np.cos(azim)+self.oecs[2]]
self.up = [0.0, up, 0.0]
def reshape(self, w, h):
"""改变窗口大小事件函数"""
self.csize = (w, h)
self.aspect = self.csize[0]/self.csize[1] if self.csize以上是关于从固定管线到可编程管线:十段代码入门OpenGL的主要内容,如果未能解决你的问题,请参考以下文章