机器学习-线性回归算法(房价预测项目)
Posted 吾仄lo咚锵
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习-线性回归算法(房价预测项目)相关的知识,希望对你有一定的参考价值。
文章目录
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。
简介
线性回归(Linear Regression)是回归任务中最常见的算法,利用回归方程对自变量和因变量进行建模,且因变量和自变量之间是线性关系而得名,从而可以根据已知数据预测未来数据,如房价预测、PM2.5预测等。
其中,只有一个自变量则称为一元线性回归,包含多个自变量则成为多元线性回归。
如下图,根据已知数据点(蓝色),建模得到红色的回归方程,表示自变量和因变量关系,从而可以输入新的自变量,得到预测值(因变量)。
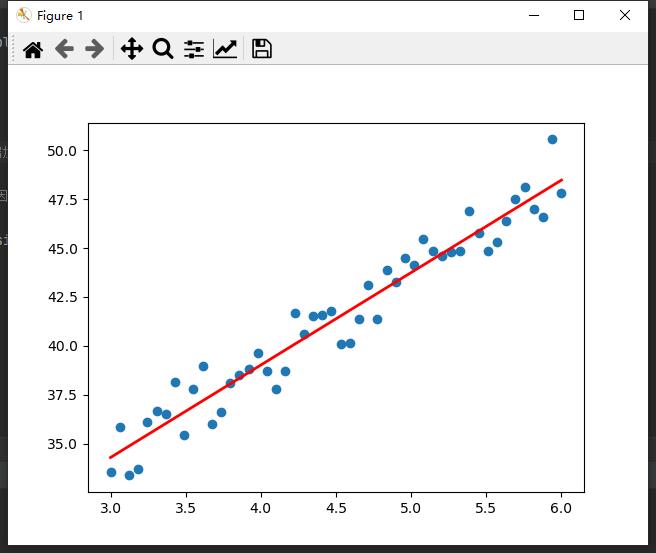
预测函数定义为:
h
(
w
)
=
w
1
x
1
+
w
2
x
2
+
⋅
⋅
⋅
+
w
d
x
d
+
b
h(w)=w_1x_1+w_2x_2+···+w_dx_d+b
h(w)=w1x1+w2x2+⋅⋅⋅+wdxd+b
向量形式为:
h
(
w
)
=
w
T
x
h(w)=\\boldw^T\\boldx
h(w)=wTx
其中
w
T
=
(
b
w
1
⋅
⋅
⋅
w
d
)
,
x
=
(
1
x
1
⋅
⋅
⋅
x
d
)
\\boldw^T=\\begingathered\\beginpmatrix b\\\\ w_1\\\\···\\\\w_d \\endpmatrix\\endgathered,\\boldx=\\begingathered\\beginpmatrix 1\\\\ x_1\\\\···\\\\x_d \\endpmatrix\\endgathered
wT=⎝⎜⎜⎛bw1⋅⋅⋅wd⎠⎟⎟⎞,x=⎝⎜⎜⎛1x1⋅⋅⋅xd⎠⎟⎟⎞
也就是说我们需要确定 w \\boldw w和 b b b的值,来构建预测函数。
假设随机初始化 w \\boldw w和 b b b后,我们得到一个预测函数 h w h_w hw,我们的目标就是希望 h w h_w hw尽可能贴近目标函数。那又要如何评价当前构建出来的模型怎么样,评价两个模型的优劣,并如何向目标函数不断靠近呢?
即使用损失函数和优化算法。
损失函数
损失函数就是定义当前函数和目标函数之间的差异,并且我们期望这个差异(损失)越小越好。
使用误差平方和SSE来表示损失,即预测值和真实值差的平方求和,该方法也称为最小二乘法,二乘即平方的意思,求最小的损失。
总损失定义为:
J
(
w
)
=
1
2
∑
i
=
1
m
(
h
w
(
x
i
)
−
y
i
)
2
=
1
2
(
x
w
−
y
)
2
J(w)=\\frac12\\sum_i=1^m(h_w(x_i)-y_i)^2=\\frac12(\\boldx\\boldw-\\boldy)^2
J(w)=21i=1∑m(hw(xi)−yi)2=21(xw−y)2
其中
h
w
(
x
i
)
h_w(x_i)
hw(xi)表示训练样本
i
i
i的预测值,
y
i
y_i
yi是训练样本
i
i
i的真实值。
也就是使下图中黄色长度之和最小。
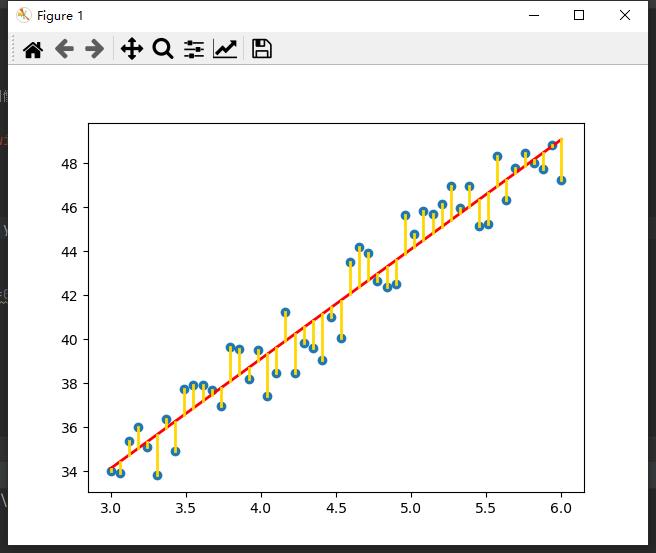
优化算法
正规方程
利用高中知识,求一个函数的最小值,我们可以求导,在导数为0处取得最小值。
这也是为什么损失函数乘以
1
2
\\frac12
21,为了求导后可以约掉。
对
w
\\boldw
w求导:
(
1
2
(
x
w
−
y
)
2
)
′
=
0
(
x
w
−
y
)
x
=
0
(
x
w
−
y
)
(
x
x
T
)
=
0
(
x
w
−
y
)
(
x
x
T
)
(
x
x
T
)
−
1
=
0
x
w
−
y
=
0
x
w
=
y
x
T
x
w
=
x
T
y
(
x
T
x
)
−
1
(
x
T
x
)
w
=
(
x
T
x
)
−
1
x
T
y
w
=
(
x
T
x
)
−
1
x
T
y
(\\frac12(\\boldx\\boldw-\\boldy)^2)^'=0\\\\ (\\boldx\\boldw-\\boldy)\\boldx=0\\\\ (\\boldx\\boldw-\\boldy)(\\boldx\\boldx^T)=0\\\\ (\\boldx\\boldw-\\boldy)(\\boldx\\boldx^T)(\\boldx\\boldx^T)^-1=0\\\\ \\boldx\\boldw-\\boldy=0\\\\ \\boldx\\boldw=\\boldy\\\\ \\boldx^T\\boldx\\boldw=\\boldx^T\\boldy\\\\ (\\boldx^T\\boldx)^-1(\\boldx^T\\boldx)\\boldw=(\\boldx^T\\boldx)^-1\\boldx^T\\boldy\\\\ \\boldw=(\\boldx^T\\boldx)^-1\\boldx^T\\boldy
(21(xw−y)2)′=0(xw−y)x=0(xw−y)(xxT)=0(xw−y)(xxT)(xxT)−1=0xw−y=0xw=yxTxw=xTy(xTx)−1(xTx)w=(xTx)−1xTyw=(xTx)−1xTy
一顿操作之后,也就是说如果
x
T
x
\\boldx^T\\boldx
xTx可逆(是正定矩阵),我们就可以直接求得最小损失对应的
w
\\boldw
w。
但是该方法适合样本特征数比较小的情况,不然矩阵太大了运算也很慢,因为复杂度是O(N3)。
使用numpy和scipy提供的矩阵运算,可以得到代码实现:
def Regres(X, Y):
x = mat(X)以上是关于机器学习-线性回归算法(房价预测项目)的主要内容,如果未能解决你的问题,请参考以下文章