浅谈梯度下降与模拟退火算法

Posted 2023-01-12 吾仄lo咚锵

文章目录

• 简介
• 全梯度下降
• 随机梯度下降
• 小批量梯度下降
• 随机平均梯度下降
• 模拟退火

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。

简介

简单来说，梯度下降就像是从山顶出发，到达最低的谷底，但下山过程中可能误入歧途，走入不是最低的谷底，即局部最优。

『梯度』是一个向量，表示函数在该点处的方向导数沿着该方向取得最大值，也就是说沿着该向量方向变化率最大，是最陡的。

梯度的大小：$|\nabla f|=\sqrt{f_x(x,y{)}^{\prime 2}+f_y(x,y{)}^{\prime 2}}$，其中$f_x(x,y{)}^{\prime }$是在点$(x,y)处$对$x$的偏导数，其中$f_y(x,y{)}^{\prime }$是在点$(x,y)处$对$y$的偏导数。偏导数可以理解为在点(x,y)处的切线对x或y的斜率。

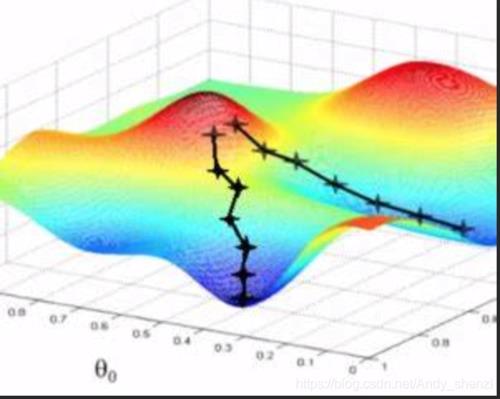
上图摘自网络。

那所谓的梯度下降法，可以理解为沿着梯度最大的反方向下山的过程。比如三维特征中，其平面图可以像是山峰和谷底，那我们就是要从山峰出发，从最陡（梯度最大）的方向进行下山，从而到达谷底取最小值，但往往可能陷入其它谷底，只取到了极小值，可以修改步长（学习率）。
$${\Theta }^1={\Theta }^0-\alpha \nabla J(\Theta )$$
其中$J$是关于$\Theta$的一个函数，设当前点位${\Theta }^0$，从这个点走一段距离的步长（也就是学习率$\alpha$），然后到达${\Theta }^1$这个点，以此迭代，最终目标是要走到$J$的最小值点，也就是谷底。

梯度下降算法中有几种方式来调节权重向量，通过为每个权重计算一个梯度，从而更新权值，使目标函数尽可能最小化。其差别在于样本的使用方式不同，包括全梯度下降算法、随机梯度下降算法、小批量梯度下降算法、随机平均梯度下降算法等，一般常用的还是随机梯度下降。

全梯度下降

---

全梯度下降算法（Full Gradient descent，FG）
所谓『全』的意思就是考虑全部的训练集样本，对其求和后取平均值。每次更新时在整个数据集上计算全部梯度，计算量较大，所以梯度下降的速度较慢。

此外，批梯度下降过程中不能同步更新模型，即在运行的过程中，不能增加新的样本数据。是在整个训练数据集上计算损失函数关于参数$\theta$的梯度。

$$\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta )$$

随机梯度下降

---

随机梯度下降算法（Stochastic Gradient descent，SG）
FG计算了全部样本，导致速度很慢且容易陷入局部最优解，故提出了SG。所谓『随机』就是每次随机带入一个样本进行计算即可，不再是全体样本误差。

使用单个样本误差更新权重，然后再随机下一个样本重复此过程，直到损失函数值停止下降，为此速度大幅提高，但是也由于每次只使用一个样本迭代，若随机到噪声样本则容易陷入局部最优解。

$$\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta ;x^{(i)};y^{(i)})$$
其中，$x_{(i)}$是训练样本$i$的特征值，$y_{(i)}$是训练样本$i$的标签值。

小批量梯度下降

---

小批量梯度下降算法（Mini-batch Gradient descent）

所谓『小批量』就是全部与一个的折中方案，兼顾了FG和SG两种方法的优点。即每次从训练样本集上随机抽取一个小样本集，在该小样本集上用FG来迭代更新权重。

抽出的小样本集所含样本点的个数（batch.size）通常设为2的幂次方，为了方便GPU加速处理。如果batch.size=1，就是SG；若batch.size=n就是FG。

$$\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta ;x^{(i:i+n)};y^{(i:i+n)})$$

（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

随机平均梯度下降

---

随机平均梯度下降算法 （Stochastic Average Gradient descent，SAG）
所谓『随机平均』是在内存中为每一个样本都维护了一个旧的梯度，随机选择第$i$个样本来更新此样本的梯度，其他样本的梯度保持不变，求得所有梯度的平均值来更新参数。

如此一来，每一轮更新仅需计算随机的一个样本梯度，同SG一样，但是收敛速度快得多，对大数据训练而言更有效。

模拟退火

---

梯度下降每次沿着梯度方向上升最大的反方向进行下降并趋于极值点，但是并不是每次沿着梯度最大的就能得到全局最优的最值点，也就是进入了其他的谷底。

可以了解一下模拟退火，每步不一定取最大，而是按照一定概率权值，在总体上以大概率向梯度下降的方向调整，但过程中接受不完美。
模拟退火背景：

物理的退火降温的过程：
给一个处于高温度的物体降温，使物体内能降到最低。
一般的思维是越快越好，尽快的温度迅速地降低。但实际上，过快地降温使得物体来不及有序地收缩，难以形成结晶，而结晶态才是物体真正内能降到最低的形态。
正确的做法，是徐徐降温，也就是退火，才能使得物体的每一个粒子都有足够的时间找到自己的最佳位置并紧密有序地排列。开始温度高的时候，粒子活跃地运动并逐渐找到一个合适的状态。在这过程中温度也会越降越低，温度低下来了，那么粒子也渐渐稳定下来，相较于以前不那么活跃了。这时候就可以慢慢形成最终稳定的结晶态了。

此外，不同学习率（步长）可能导致完全不同的结果。
若过大，则可能来回震荡，无法到达最优点；
若过小，则可能陷入局部最优；
合适的学习率才能取到全局最优。一般设置为0.1左右。

import numpy as np
import matplotlib.pyplot as plt


def func(x):  # 函数定义
    return x ** 4 + 2 * x ** 3 - 3 * x ** 2 - 3 * x


def grad_func(x):  # 求导
    return 4 * x ** 3 + 6 * x ** 2 - 6 * x - 3


if __name__ == "__main__":
    x = np.linspace(-3, 1.9)  # 定义域[-3,1.9]
    fx = func(x)
    plt.plot(x, fx, '--')  # 虚线画出曲线

    eta = 0.08  # 学习率
    x0 = 1.8  # 初始值（山顶）
    record_x = []
    record_y = []
    for i in range(50):
        y0 = func(x0)
        record_x.append(x0)
        record_y.append(y0)
        x0 -= eta * grad_func(x0)  # 梯度下降
    # 可视化
    plt.title("学习率=0.08")
    plt.scatter(record_x, record_y, marker='x', color="red")
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.show()

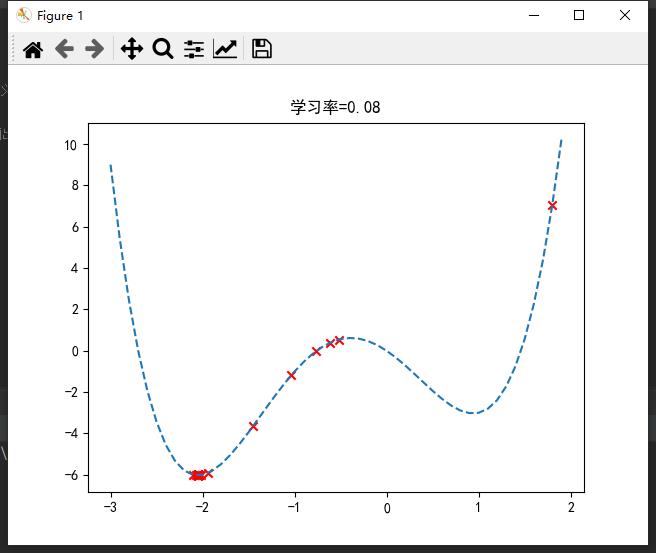
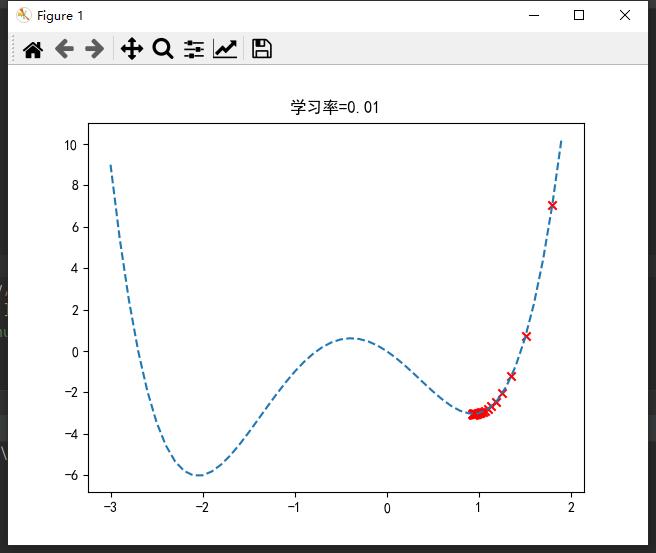
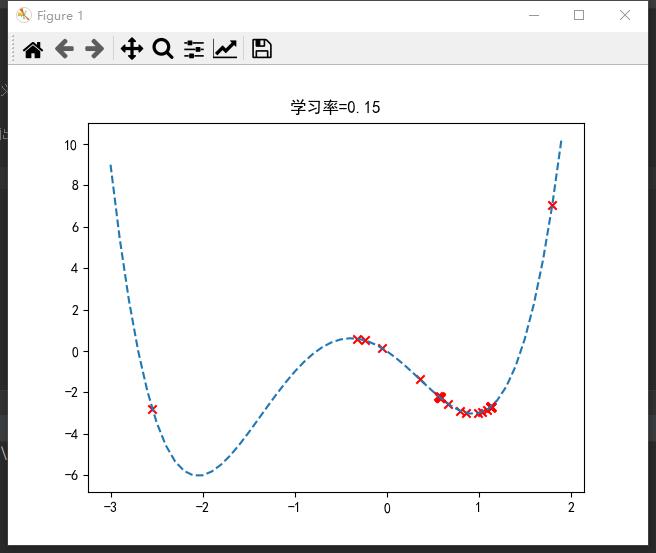
在sklearn库中，封装了SGD*随机梯度下降算法的应用，如分类SGDClassifier()、回归SGDRegressor()等(☆▽☆)。

原创不易，请勿转载（本不富裕的访问量雪上加霜 ）
博主首页：https://wzlodq.blog.csdn.net/
来都来了，不评论两句吗👀
如果文章对你有帮助，记得一键三连❤