MATLAB | 趣味编程——线条艺术：柔线球

Posted 2023-01-11 slandarer

一期趣味编程，虽然代码总长度只有45行，但是！考验大家电脑性能的时候到了！本期趣味编程复刻的是Oliver Brotherhood大佬的Processing作品Iris：

非常好看的像薄纱似的线条艺术！！

---

原理及代码讲解

以下代码讲解并非代码实际排列顺序，本文下一部分会提供完整代码。

配色

tPntNum=3000;
tList=1:tPntNum;
% 渐变颜色
% #046380, #16193B, #35478C, #4E7AC7, #7FB2F0, #ADD5F7
CList=[4 99 128;22 25 59;53 71 140;78 122 199;127 178 240;173 213 247]./255;
ti=linspace(1,tPntNum,size(CList,1))';
CList=[interp1(ti,CList(:,1),tList,'linear')',...
       interp1(ti,CList(:,2),tList,'linear')',...
       interp1(ti,CList(:,3),tList,'linear')'];

3000根线颜色各不相同，我们其实只是拿了6种颜色线性渐变插值到3000多种颜色：

贝塞尔曲线

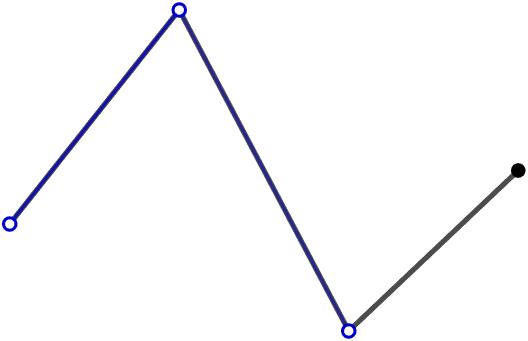
这里是是用的四个点的三次贝塞尔曲线，就是四个点，顺序挨着的点两两相连，有三条线段，取其将线段分成k:(1-k)部分的点，总共有三个点，再次顺序挨着的点两两相连，有两条线段，取其将线段分成k:(1-k)部分的点，总共有两个点，两点连线再次取将线段分成k:(1-k)部分的点就得到了贝塞尔曲线在参数等于k时候的点：

% 贝塞尔函数
    function pnts=bezierCurve(pnts,N)
        t=linspace(0,1,N);
        p=size(pnts,1)-1;
        coe1=factorial(p)./factorial(0:p)./factorial(p:-1:0);
        coe2=((t).^((0:p)')).*((1-t).^((p:-1:0)'));
        pnts=(pnts'*(coe1'.*coe2))';
    end

样点获取

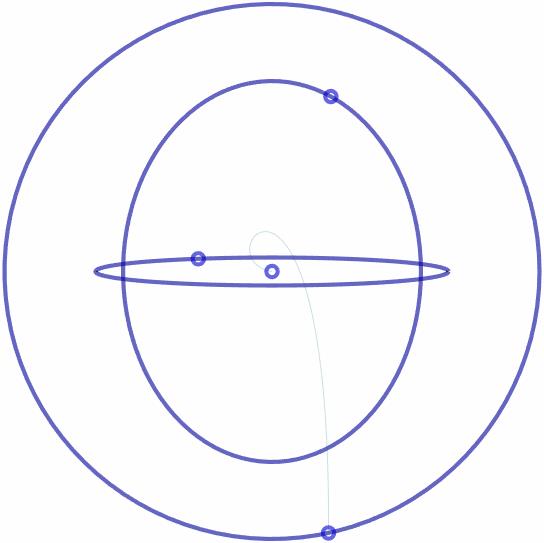
一共需要四个点构造贝塞尔曲线，其中第一个点就是原点，第四个点是半径为1的圆形上随机游动的点，另外俩点是在随机a\\b值的俩椭圆上：

% 随机椭圆半径
A1=rand(1,1);B1=rand(1,1);
A2=rand(1,1);B2=rand(1,1);
for i=1:3000
    X=[0;A1*cos(thetaList1(i));A2*cos(thetaList2(i));cos(thetaList3(i))];
    Y=[0;B1*sin(thetaList1(i));B2*sin(thetaList2(i));sin(thetaList3(i))];
    bezierPnts=bezierCurve([X,Y],100);
    plot(bezierPnts(:,1),bezierPnts(:,2),'Color',[CList(i,:),.2],'LineWidth',.5)
    pause(.01)
end

随机角度

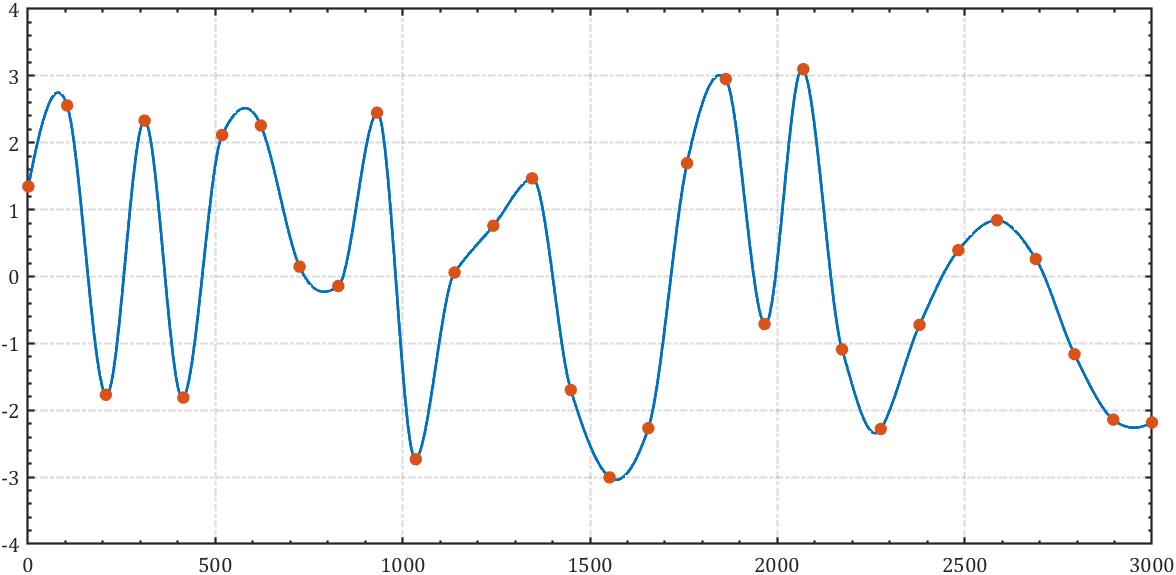
我们需要随机的角度足够平滑的变换，因此虽然理论上一共三个圆\\椭圆需要3000x3个角度值，但对于每一个圆\\椭圆我们只生成了30个随机点，之后将其插值为3000个角度：

randPntNum=30;
tPntNum=3000;
tList=1:tPntNum;
% 生成连续随机角度
randList1=(rand(1,randPntNum)-.5).*2.*3.15;
randList2=(rand(1,randPntNum)-.5).*2.*3.15;
randList3=(rand(1,randPntNum)-.5).*2.*3.15;
thetaList1=interp1(linspace(1,tPntNum,randPntNum),randList1,tList,'makima');
thetaList2=interp1(linspace(1,tPntNum,randPntNum),randList2,tList,'makima');
thetaList3=interp1(linspace(1,tPntNum,randPntNum),randList3,tList,'makima');

---

完整代码

function Iris
% 灵感来自 Oliver Brotherhood 的 Processing 作品 Iris
% 由 slandarer 使用 MATLAB 进行复刻
randPntNum=30;
tPntNum=3000;
tList=1:tPntNum;
% 生成连续随机角度
randList1=(rand(1,randPntNum)-.5).*2.*3.15;
randList2=(rand(1,randPntNum)-.5).*2.*3.15;
randList3=(rand(1,randPntNum)-.5).*2.*3.15;
thetaList1=interp1(linspace(1,tPntNum,randPntNum),randList1,tList,'makima');
thetaList2=interp1(linspace(1,tPntNum,randPntNum),randList2,tList,'makima');
thetaList3=interp1(linspace(1,tPntNum,randPntNum),randList3,tList,'makima');
% 渐变颜色
% #046380, #16193B, #35478C, #4E7AC7, #7FB2F0, #ADD5F7
CList=[4 99 128;22 25 59;53 71 140;78 122 199;127 178 240;173 213 247]./255;
ti=linspace(1,tPntNum,size(CList,1))';
CList=[interp1(ti,CList(:,1),tList,'linear')',...
       interp1(ti,CList(:,2),tList,'linear')',...
       interp1(ti,CList(:,3),tList,'linear')'];
% 坐标区域修饰
ax=gca;hold on
ax.XLim=[-1,1];
ax.YLim=[-1,1];
ax.XColor='none';
ax.YColor='none';
ax.DataAspectRatio=[1,1,1];
% 随机椭圆半径
A1=rand(1,1);B1=rand(1,1);
A2=rand(1,1);B2=rand(1,1);
for i=1:3000
    X=[0;A1*cos(thetaList1(i));A2*cos(thetaList2(i));cos(thetaList3(i))];
    Y=[0;B1*sin(thetaList1(i));B2*sin(thetaList2(i));sin(thetaList3(i))];
    bezierPnts=bezierCurve([X,Y],100);
    plot(bezierPnts(:,1),bezierPnts(:,2),'Color',[CList(i,:),.2],'LineWidth',.5)
    pause(.01)
end
% 贝塞尔函数
    function pnts=bezierCurve(pnts,N)
        t=linspace(0,1,N);
        p=size(pnts,1)-1;
        coe1=factorial(p)./factorial(0:p)./factorial(p:-1:0);
        coe2=((t).^((0:p)')).*((1-t).^((p:-1:0)'));
        pnts=(pnts'*(coe1'.*coe2))';
    end
end

---

更多绘制效果展示