优化组合基于matlab多种群混沌蚁群算法求解机组组合优化问题含Matlab源码 2017期
Posted 海神之光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优化组合基于matlab多种群混沌蚁群算法求解机组组合优化问题含Matlab源码 2017期相关的知识,希望对你有一定的参考价值。
⛄一、多种群混沌蚁群算法求解机组组合优化问题
0 引言
机组组合问题(Unit Commitment,UC)又称开停机计划,是电力系统解决优化潮流(OPF)、经济调度(ED)进而实现自动发电控制(AGC)、自动电压控制(AVC)的前提。机组组合问题具有高维数、非凸、离散、非线性的特点,在数学上为NP-Hard问题。实际中最多地运用于解决这类问题的方法有:优先级表法[1]、混合整数规划法[2]、拉格朗日松弛法[3]、动态规划法[4]等。随着启发式方法的发展,人工智能算法也被应用于机组组合问题中,其中包括:蚁群算法[5]、粒子群算法[6]、模拟退火算法[7]、遗传算法[8]、免疫算法[9]等。
蚁群算法(Ant Colony Optimization algorithm,ACO)因其高度并行性、合作性和鲁棒性被成功运用于求解多种组合优化问题当中。多种群蚁群算法(Multi colony ant Optimization algorithm,MCAO)将蚁群分类,对不同种类蚁群赋予不同的任务,通过各类蚁群之间的信息交流与合作来提高算法的计算效率以及解的质量。本文提出的多种群混沌蚁群算法(Multi colony chaotic ant Optimization algorithm,MCCAO)将蚁群分为搜索蚁、侦察蚁和工蚁。在蚁群算法选择路径过程中为信息素加入混沌量,使得蚁群在路径搜索时有更多的机会脱离局部最优,发现最优解。
1 机组组合问题的描述
机组组合的目标函数通常为系统运行成本G最小,其表达式为
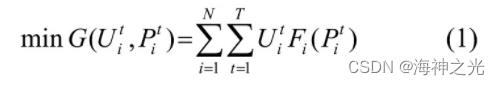
其中:Uit为0,1变量,表示第i台机组t时刻机组开关机状态;Fi(Pit)一般可以表示为
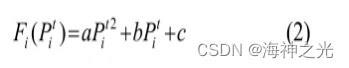
机组组合问题的约束条件可以分为系统约束和机组特性约束。系统约束包括系统功率平衡约束、备用约束,如式(3)式(4)所示。机组特性约束包括机组输出功率约束、机组爬坡速率约束、最小开停机时间约束,如式(5)式(8)所示。

其中:Uit含义与式(1)中相同;iPt为第i台机组在t时段的出力;PDt为时段t系统负荷;SDt为时段t的备用要求;为机组i的出力上/下限;Rui和Rdi为机组i每个时段允许可调的出力上/下限;T1i和T2i为机组i的最小开机时间和最小关机时间[9]。
2 多种群蚁群算法
2.1 种群间合作的作用原理
多种群蚁群算法把蚁群分为:搜索蚁,侦察蚁和工蚁三个蚁群。
搜索蚁的任务是寻找最优解。侦察蚁的作用是在搜索蚁已经找到的优质路径以外的路径中寻优,这样做的目的是尽可能使得蚁群算法避免落入局部最优。在多种群蚁群算法中,工蚁是整个蚁群算法的核心。工蚁的工作是做最优解的分析、总结以及信息素的调整。搜索蚁和侦察蚁把各自找到的路径信息传递给工蚁,工蚁找出收到信息中的最优解,形成最优解集。之后对最优解集中的解做整理、加权,调整最优解集的信息。最后根据得到的最优解集信息,为搜索蚁和侦察蚁调整信息素。
多种群蚁群算法各种群之间的信息交换机制可以用图1表示。
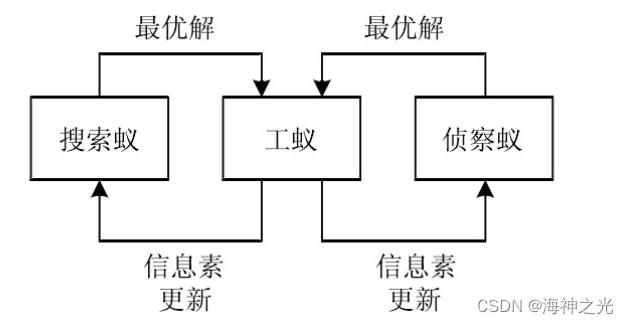
图1 多种群蚁群算法信息交互原理
2.2 搜索蚁、侦查蚁的路径选择原理
搜索蚁和侦查蚁采用相同的路径选择原理。在运用蚁群算法解决机组组合优化问题时,把某时段机组的一种随机组合状态当做蚂蚁在该时段的一条候选路径,蚁群选择转移路径的概率公式为
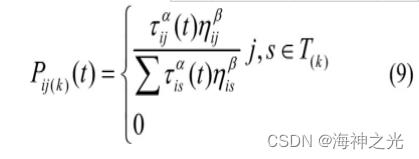
式中:τij(t)表示t时刻路径ij上的信息素量;ηij为与解决问题相关的启发式信息,在机组组合优化中可选为t时刻运行费用的倒数;ij表示在k时段里从i到j的一条路径;is表示在k时段里从i出发的任意一条候选路径;α,β分别表示蚂蚁在运动过程中所积累的信息及启发式因子在蚂蚁选择路径过程中所起作用的重要程度;T(k)为k时段的候选路径表集合,在机组组合优化中为通过开停机时间约束和爬坡约束筛选后的可选机组组合办法所组成的集合。
2.3 混沌量的引入
混沌优化是运用混沌序列的随机性、遍历性和初值敏感性来提高随机优化算法的效率。Logistic序列是一种常用的混沌序列,它的表达式描述为
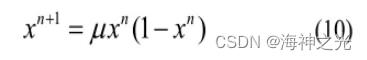
其中,μ为常数,取值在区间[3.46,4]上。当μ=4,x取在[0,1]上时,Logistic完全处于混沌状态。
本文提出的多种群蚁群算法中搜索蚁和侦察蚁按照式(9)来选取路径,与基本蚁群算法不同的是在运用式(9)之前,对信息素做如下混沌的扰动。
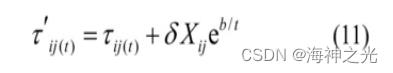
其中:Xij为混沌扰动,由混沌系统Logistic映射得到;δ为相关系数;b为扰动尺度。
需要指出的是,本文所用到的混沌优化实质上最后并没有改变信息素的调整,混沌扰动只是在选取路径过程起作用。这样做一方面维护了蚁群算法在寻优过程中知识积累的准确性;另一方面也使得路径选择加入了一定的随机性。
2.4 工蚁的作用原理
从多种群蚁群算法种群间合作原理中可以看出,工蚁是多种群混沌蚁群算法的核心。工蚁在接受搜索蚁和侦察蚁得到的路径后,对路径进行筛选,找出较优的一组路径,形成最优解集,并将最优解集中的最优解复制加权。然后根据最优解集中的路径,利用全局信息素更新规则来为搜索蚁和侦查蚁更新路径上信息素信息。搜索蚁信息素更新公式为

式中:0<ρ<1表示信息素的挥发因子,以减少历史记忆对选择的影响;Q为常数表示信息素强度。分析以上公式可以看出,在所有候选路径中,某条路径上的信息素越多且路径越短,则蚂蚁选择该路径的概率也越大。
为侦察蚁更新信息素时,所用到的信息素调整方式与式(12)不同,改做用式(15)来调整。
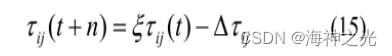
其中,ξ是恢复系数,为常数。从式(15)中容易看出:与搜索蚁不同,侦察蚁通过减少在最优路径上信息素的含量来避开已经找到的最优路径。其他路径上信息素含量的相对提高使蚁群有更多的机会探索没有搜索到的区域,这样做可以使蚁群算法避免落入局部最优。
3 多种群蚁群算法流程
多种群蚁群算法流程如图2,步骤描述如下:
(1)初始化。读取系统信息,初始化各参数,计迭代次数Nt=0。
(2)Nt=Nt+1,搜索蚁和侦查蚁按照式(8)、式(13)选取路径寻优。在找到的路径中,每组选取解中前n个最优解。
(3)工蚁接收搜索蚁和侦察蚁每次寻优得到的各自前n个最优解。将这2n个结果再排序,找到前n个最优解,将这n个最优解归入最优集Tbest。
(4)将最优解复制m份,其中m=λn(0<λ<1)。
(5)将Tbest中最优解重新排序,找到最优的n个解。
(6)为搜索蚁和侦察蚁更新信息素。搜索蚁的信息素更新方法采用式(12)式(14)基本蚁群全局信息素更新的算法。侦察蚁采用式(13)式(15)来更新信息素。
(7)判断是否已经达到收敛要求。如果是,则输出最优解;如果不是,则返回(2)。
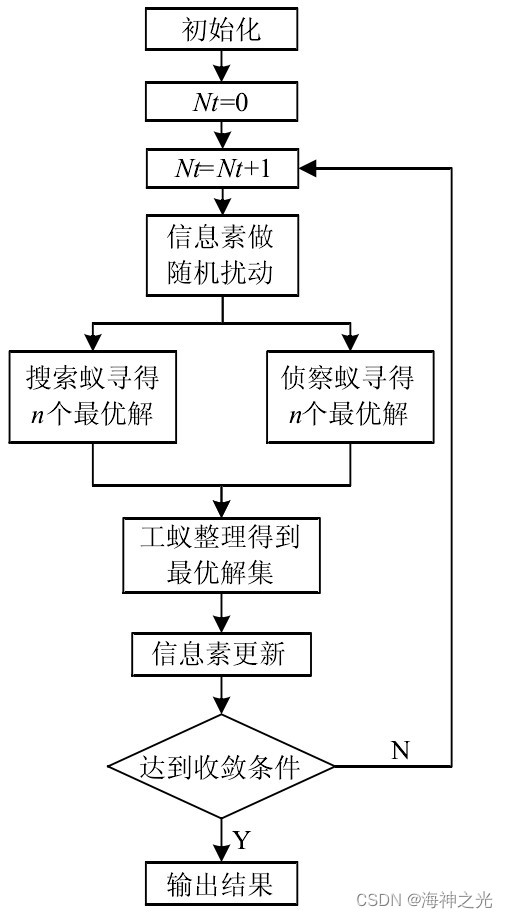
图2 多种群蚁群算法流程
⛄二、部分源代码
clear
clc
n=33;%n=input(‘请输入节点数’);
b=32;%b=input(‘请输入支路数’);
disp(‘请输入支路阻抗和节点功率矩阵,第一列存支路号,第二列存首节点号,第三列存尾节点号,第四列存支路自阻抗,第五列存尾节点给定功率’);
Sb=10;%基准功率
Ub=12.66;%基准电压
Zb=Ub^2/Sb%基准阻抗
Z=[1,0,1,0.0922/Zb+i0.047/Zb,100/(Sb1000)+i60/(Sb1000)
2,1,2,0.4930/Zb+i0.2511/Zb,90/(Sb1000)+i40/(Sb1000)
3,2,3,0.3660/Zb+i0.1864/Zb,120/(Sb1000)+i80/(Sb1000)
4,3,4,0.3811/Zb+i0.1941/Zb,60/(Sb1000)+i30/(Sb1000)
5,4,5,0.8190/Zb+i0.7070/Zb,60/(Sb1000)+i20/(Sb1000)
6,5,6,0.1872/Zb+i0.6188/Zb,200/(Sb1000)+i100/(Sb1000)
7,6,7,0.7114/Zb+i0.2351/Zb,200/(Sb1000)+i100/(Sb1000)
8,7,8,1.0300/Zb+i0.7400/Zb,60/(Sb1000)+i20/(Sb1000)
9,8,9,1.0440/Zb+i0.7400/Zb,60/(Sb1000)+i20/(Sb1000)
10,9,10,0.1966/Zb+i0.0650/Zb,45/(Sb1000)+i30/(Sb1000)
11,10,11,0.3744/Zb+i0.1238/Zb,60/(Sb1000)+i35/(Sb1000)
12,11,12,1.4680/Zb+i1.1550/Zb,60/(Sb1000)+i35/(Sb1000)
13,12,13,0.5416/Zb+i0.7129/Zb,120/(Sb1000)+i80/(Sb1000)
14,13,14,0.5910/Zb+i0.5260/Zb,60/(Sb1000)+i10/(Sb1000)
15,14,15,0.7463/Zb+i0.5450/Zb,60/(Sb1000)+i20/(Sb1000)
16,15,16,1.2890/Zb+i1.7210/Zb,60/(Sb1000)+i20/(Sb1000)
17,16,17,0.3720/Zb+i0.5740/Zb,90/(Sb1000)+i40/(Sb1000)
18,1,18,0.1640/Zb+i0.1565/Zb,90/(Sb1000)+i40/(Sb1000)
19,18,19,1.5042/Zb+i1.3554/Zb,90/(Sb1000)+i40/(Sb1000)
20,19,20,0.4095/Zb+i0.4784/Zb,90/(Sb1000)+i40/(Sb1000)
21,20,21,0.7089/Zb+i0.9373/Zb,90/(Sb1000)+i40/(Sb1000)
22,2,22,0.4512/Zb+i0.3083/Zb,90/(Sb1000)+i50/(Sb1000)
23,22,23,0.8980/Zb+i0.7091/Zb,420/(Sb1000)+i200/(Sb1000)
24,23,24,0.8960/Zb+i0.7011/Zb,420/(Sb1000)+i200/(Sb1000)
25,5,25,0.2030/Zb+i0.1034/Zb,60/(Sb1000)+i25/(Sb1000)
26,25,26,0.2842/Zb+i0.1447/Zb,60/(Sb1000)+i25/(Sb1000)
27,26,27,1.0590/Zb+i0.9337/Zb,60/(Sb1000)+i20/(Sb1000)
28,27,28,0.8042/Zb+i0.7006/Zb,120/(Sb1000)+i70/(Sb1000)
29,28,29,0.5075/Zb+i0.2585/Zb,200/(Sb1000)+i600/(Sb1000)
30,29,30,0.9744/Zb+i0.9630/Zb,150/(Sb1000)+i70/(Sb1000)
31,30,31,3105/Zb+i0.3619/Zb,210/(Sb1000)+i100/(Sb1000)
32,31,32,0.3410/Zb+i0.5362/Zb,60/(Sb1000)+i40/(Sb1000)]
k=0;
V=ones(n,1);
t=0;
%迭代开始处
while t<b & k<1000
%算节点注入电流
x1=Z(b,3);x=x1-n;
for l=1:b
j=Z(l,3);
ua=V(j+1,1);
I(j,1)=conj(Z(j,5)/ua);
end
⛄三、运行结果
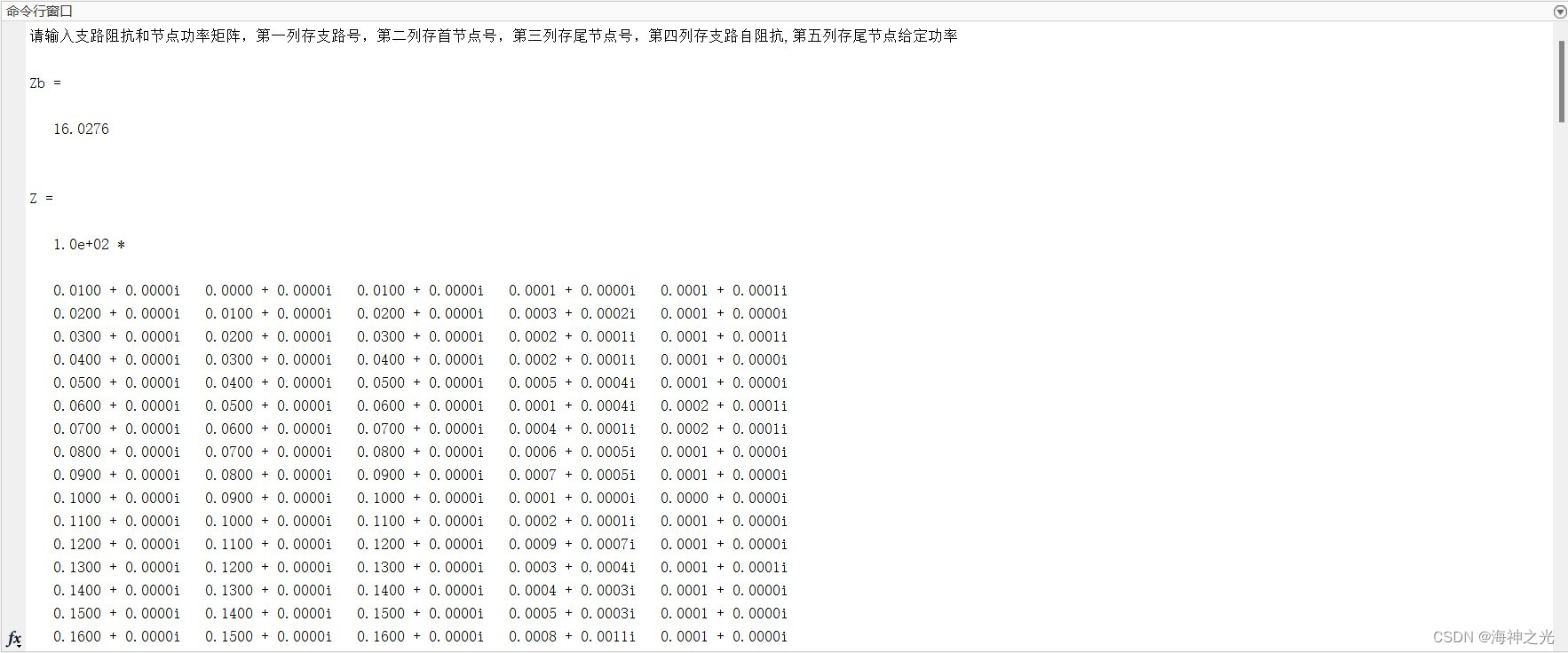
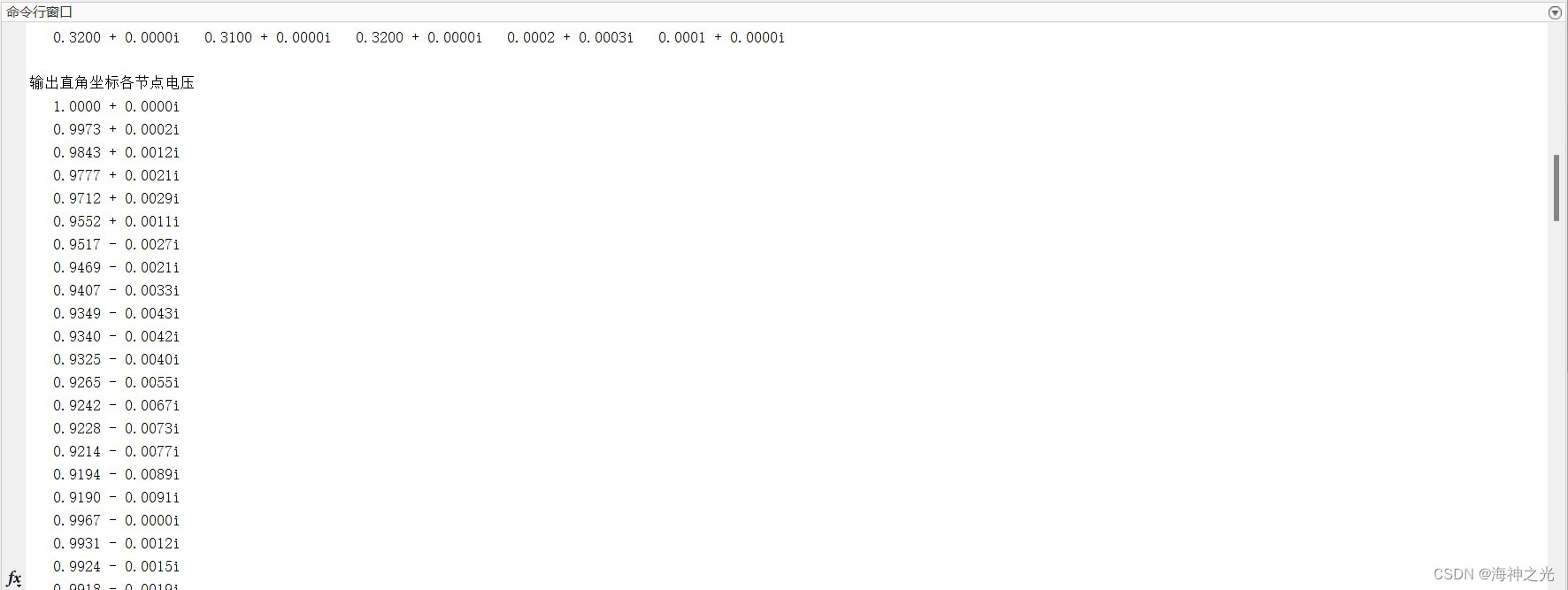



⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]李颖浩,郭瑞鹏.求解机组组合问题的多种群混沌蚁群算法[J].电力系统保护与控制. 2012,40(09)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于优化组合基于matlab多种群混沌蚁群算法求解机组组合优化问题含Matlab源码 2017期的主要内容,如果未能解决你的问题,请参考以下文章