深度学习常见概念字典（感知机全连接层激活函数损失函数反向传播过拟合等）

Posted 2022-12-26 smile-yan

这一章的所有内容均是为了进入深度学习具体的某某网络而准备的，简单但是非常有必要。

1. 神经网络（neural networks）的基本组成

1.1 神经元（neuron）

神经元（neuron） 是神经网络（neural networks）中最基本的单位。神经网络与神经元的概念均是借鉴于生物学，可以简单理解为：如果某神经元的点位超过了“阈值（threshold）”，那么它就会被激活，将 “兴奋” 的状态以电位信息的方式发送给其他神经元或输出。

1.2 感知机（Perceptron）

感知机（Perceptron） 由两层神经元组成（输入层与输出层），感知机模型的结构如图所示：

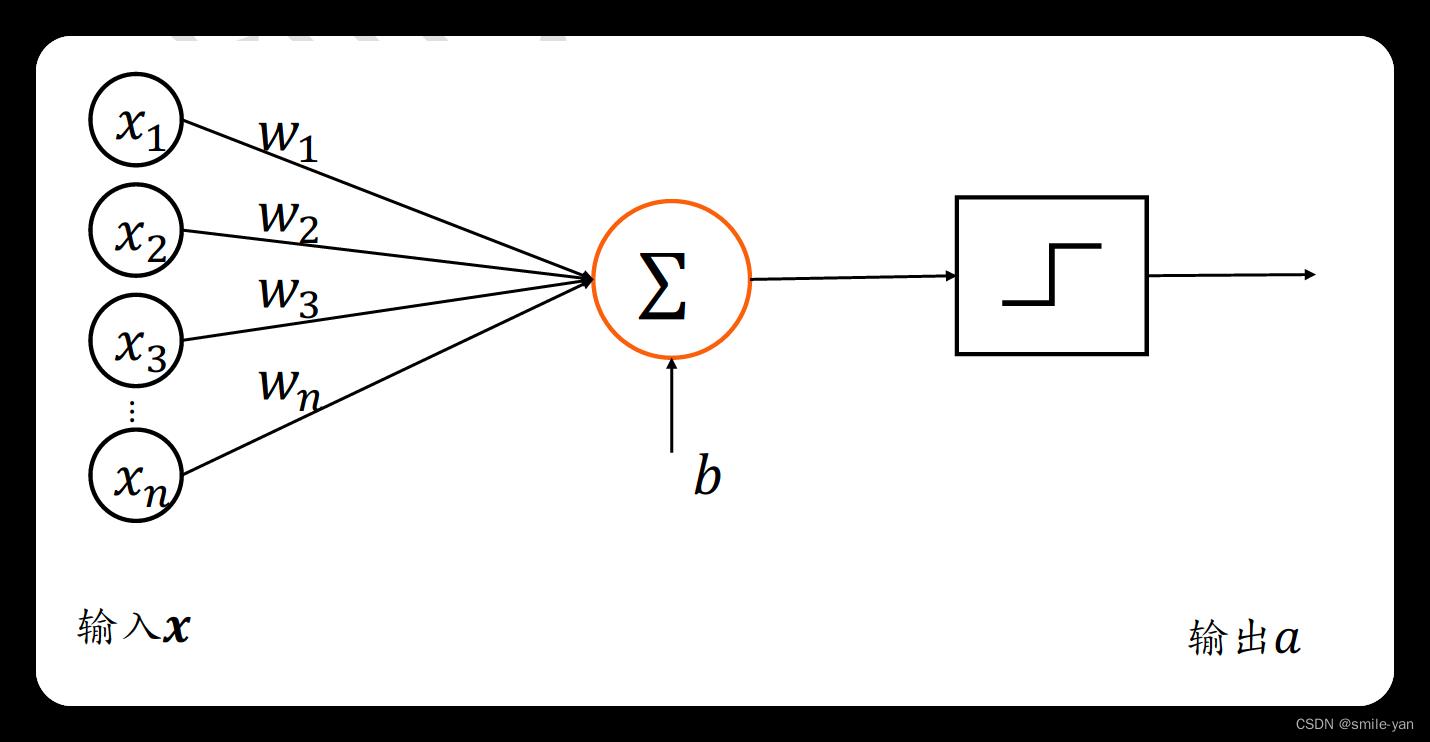
对应的公式为：

$$z=w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n+b\text{\hspace{1em}(1.2.1)}$$

对应的表示为向量的形式为：

$$z={\text{w}}^{\text{T}}\text{x}+b\text{\hspace{1em}(1.2.2)}$$

摘录自 《Tensorflow 深度学习》 龙良曲 著 清华大学出版社

1.3 全连接层（fully connected layers，FC）

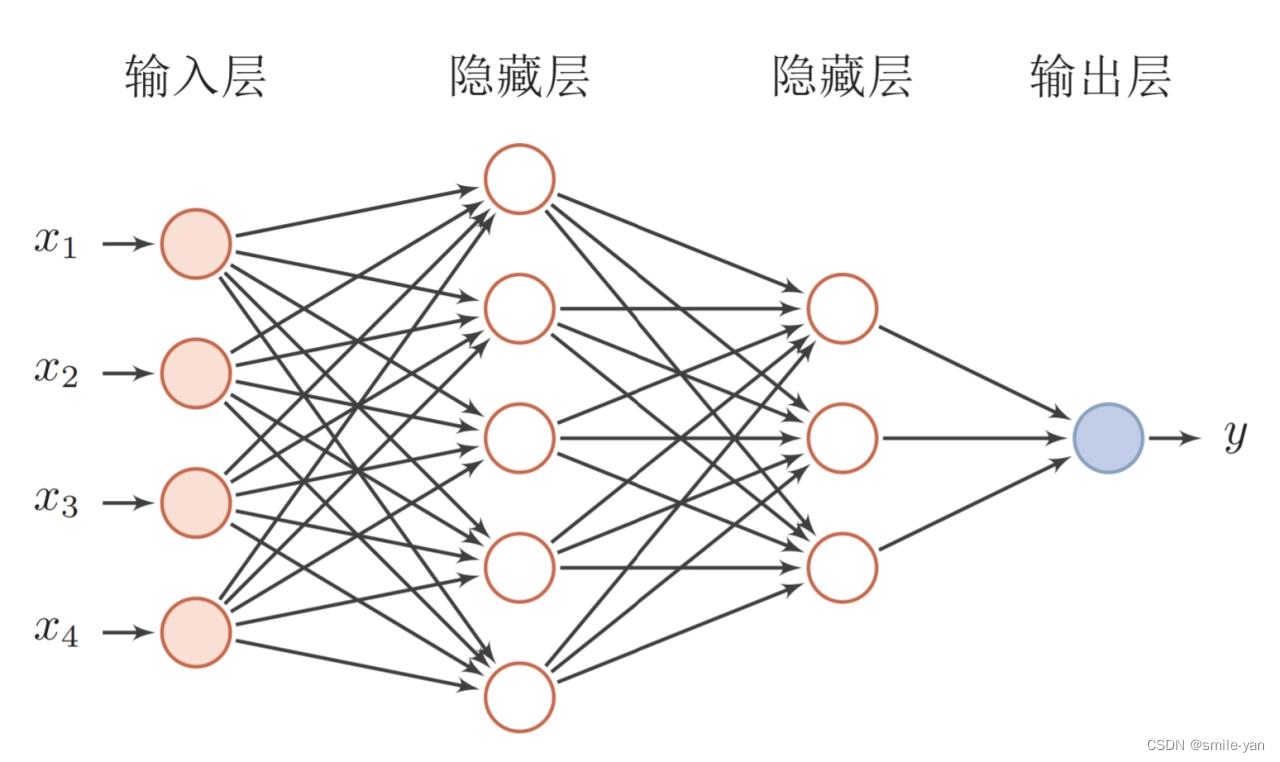
全连接层（fully connected layers，FC），是每一个结点都与上一层的所有结点相连，用来把前边提取到的特征综合起来。由于其全相连的特性，一般全连接层的参数也是最多的。

如下图所示，我们把左边部分看作输入特征向量，右边的部分则是神经网络中的一个全连接层。

1.4 前馈神经网络（feedforward neural network，FNN）

前馈神经网络（feedforward neural network，FNN），是一种最简单的神经网络，各神经元分层排列，每个神经元只与前一层的神经元相连。接收前一层的输出，并输出给下一层，各层间没有反馈。

前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元。在此种神经网络中，各神经元可以接收前一层神经元的信号，并产生输出到下一层。

摘录自 百度百科

2. 神经元之间的数据传播

2.1 激活函数（Activation functions）

激活函数（Activation functions） ：建立神经元的输入与输出之间映射关系的函数。

为什么要用激活函数 ：

• 不使用激活函数时，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。
• 使用激活函数给神经元引入了非线性因子，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

参考 百度百科-激活函数

2.2 正向传播算法（Forward propagation algorithm）

正向传播算法（Forward propagation algorithm）：沿着从输入层到输出层的顺序，依次计算并存储神经网络的中间变量。

2.3 损失函数（loss function）

损失函数（loss function）别称代价函数（coss function）：在神经网络中，损失函数一般是指用来计算模型的预测值与真实值之间的差异的计算方法。由于不同算法模型的数学原理不同，对应的损失函数也可能存在一定程度的差异。

2.4 logits 是什么

logits 指的是分类模型生成的原始（非标准化）预测向量，通常传递给标准化函数。如果模型正在解决多类分类问题，则 logit 通常会成为softmax函数的输入。然后，softmax函数生成（归一化）概率向量，每个可能的类具有一个值。

不少论文、视频常常提到 logit 的使用，这里也记录一下 logit 是什么。
参考 logit | 博客 1 | 博客 2

2.5 反向传播（Backpropagation, BP）算法

反向传播算法，简称BP算法，适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。

摘录自百度百科 反向传播算法

参考 深度学习——反向传播（Backpropagation）

2.6 导数（Derivative）与梯度

导数在高中的时候便开始学习，大学的时候也继续深入学习，这里不再介绍，推荐参考 百度百科导数。

梯度的概念可以参考 百度百科 梯度。

总结

更多的概念性内容会在后面继续整理，主要目的是用来回答 “什么是什么” 以及 “什么的作用是什么” 这类的问题。保证自己有一个初步的了解对今后的学习很有必要。