日常系列LeetCode《18·二叉树3》
Posted 常某某的好奇心
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了日常系列LeetCode《18·二叉树3》相关的知识,希望对你有一定的参考价值。
数据规模->时间复杂度
<=10^4 😮(n^2)
<=10^7:o(nlogn)
<=10^8:o(n)
10^8<=:o(logn),o(1)
内容

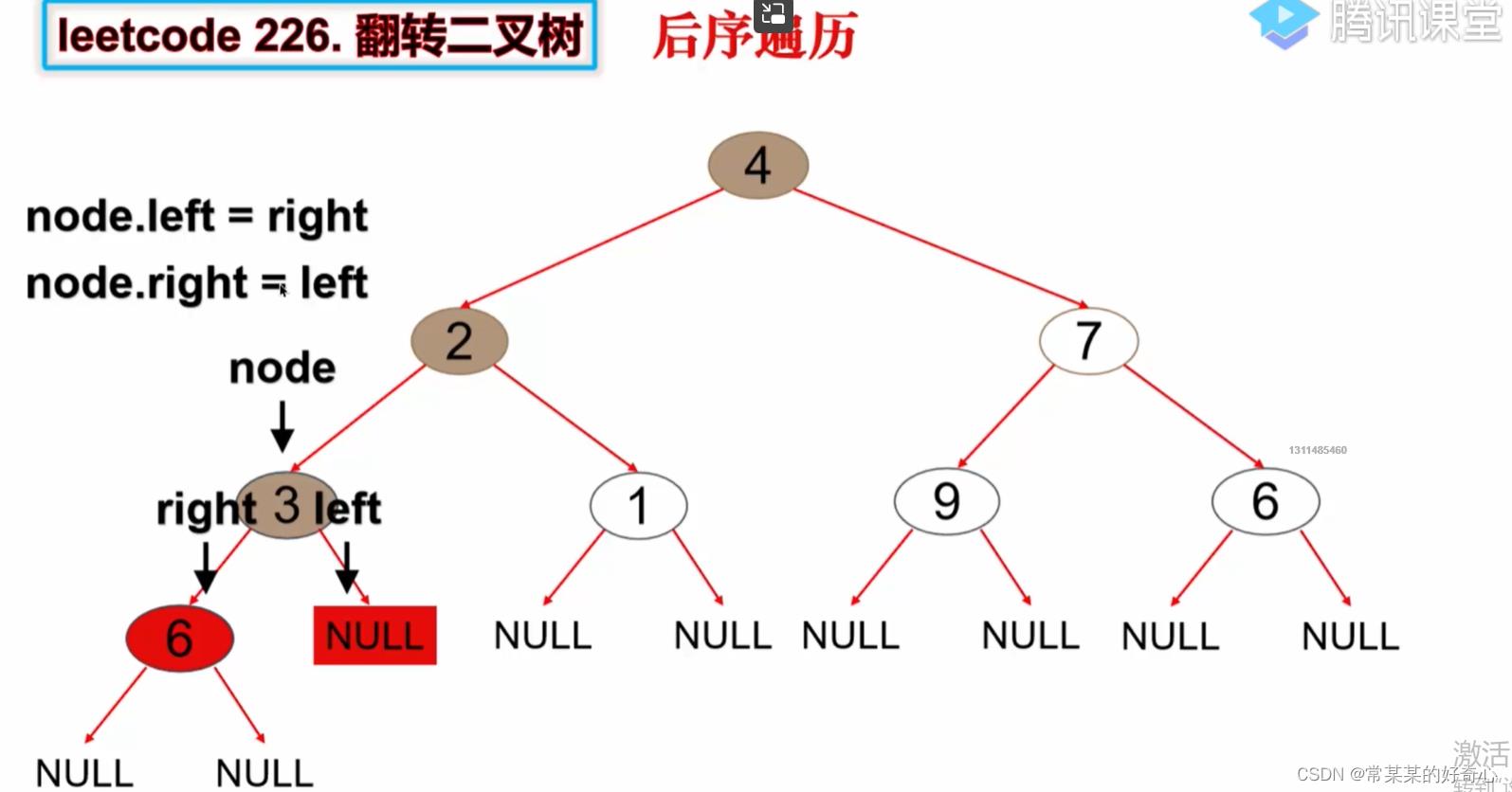
lc 226【剑指 226】【top100】:翻转二叉树
https://leetcode.cn/problems/invert-binary-tree/
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
return self.postorder(root)
def postorder(self,node):
#
if not node:return None
if not node.left and not node.right:return node
#
left=self.postorder(node.left)
right=self.postorder(node.right)
#
node.left=right
node.right=left
return node
lc 617【top100】:合并二叉树
https://leetcode.cn/problems/merge-two-binary-trees/
提示:
两棵树中的节点数目在范围 [0, 2000] 内
-10^4 <= Node.val <= 10^4
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if not root1:return root2
if not root2:return root1
#
newnode=TreeNode(root1.val+root2.val)
newnode.left=self.mergeTrees(root1.left,root2.left)
newnode.right=self.mergeTrees(root1.right,root2.right)
return newnode
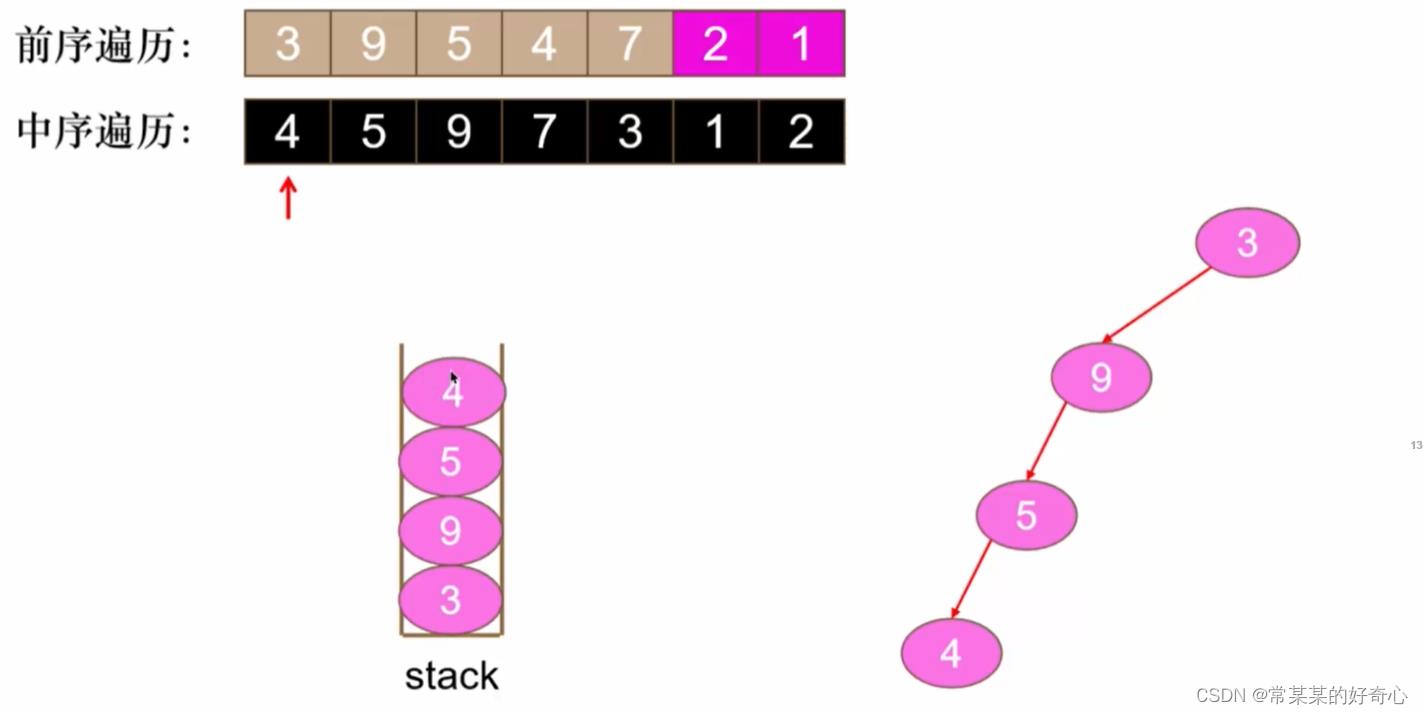
lc 105【剑指 7】【top100】:从前序与中序遍历序列构造二叉树
https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
#方案一:迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
#
Map=
for i in range(len(inorder)):
Map[inorder[i]]=i
#
stack=deque()
root=TreeNode(preorder[0])
stack.append(root)
#
index=0
for i in range(1,len(preorder)):
childnode=TreeNode(preorder[i])
parentnode=stack[-1] #指stack.peek()
#
if Map[childnode.val]<Map[parentnode.val]:
parentnode.left=childnode
stack.append(parentnode.left)
else:
#key:找右节点的父节点
while stack and inorder[index]==stack[-1].val:
parentnode=stack.pop()
index+=1
parentnode.right=childnode
stack.append(parentnode.right)
return root
#方案二:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
#
self.preorder=preorder
self.Map=
for i in range(len(inorder)):
self.Map[inorder[i]]=i
#
self.index=0
return self.build(0,len(inorder)-1)
def build(self,left,right):
if left>right:return None
###key
#nonlocal index
node = TreeNode(self.preorder[self.index])
self.index += 1
mid = self.Map[node.val]
#
node.left=self.build(left,mid-1)
node.right=self.build(mid+1,right)
return node
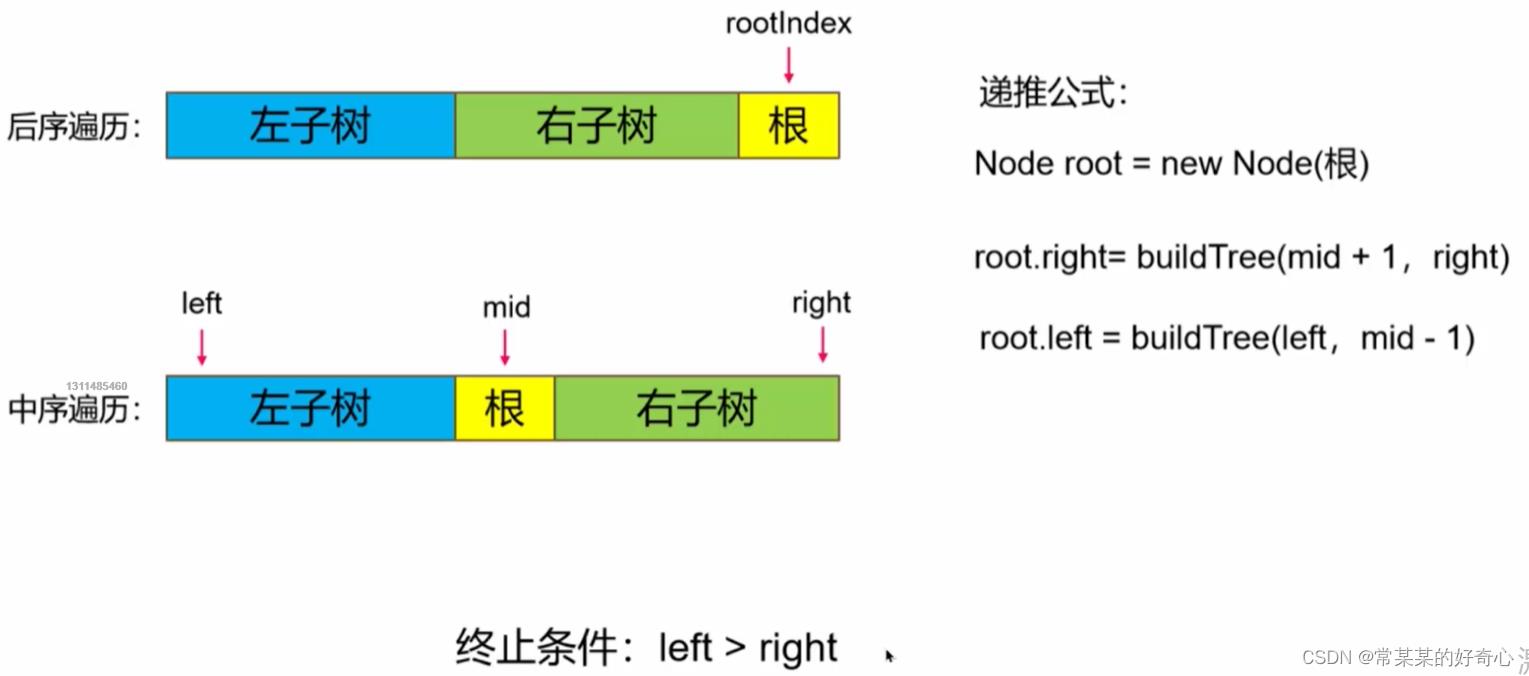
lc 106 :从中序与后序遍历序列构造二叉树
https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
提示:
1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
#
self.postorder=postorder
self.Map=
for i in range(len(inorder)):
self.Map[inorder[i]]=i
#
self.index=len(postorder)-1
return self.build(0,len(inorder)-1)
def build(self,left,right):
if left>right:return None
###key
#nonlocal index
node = TreeNode(self.postorder[self.index])
self.index-=1
mid = self.Map[node.val]
#
node.right=self.build(mid+1,right)
node.left=self.build(left,mid-1)
return node
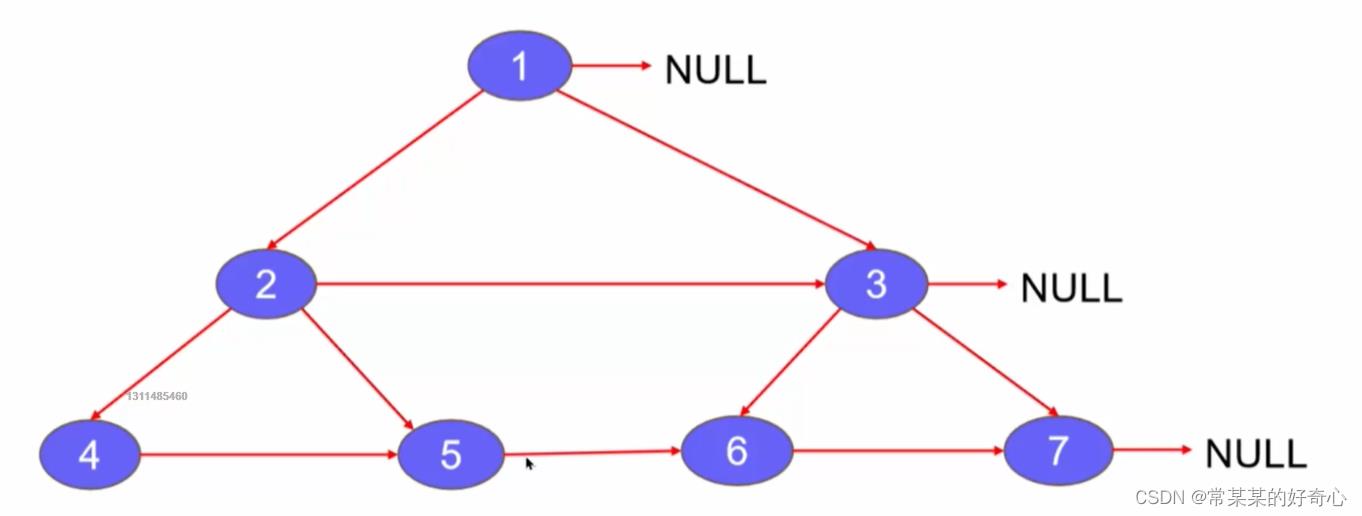
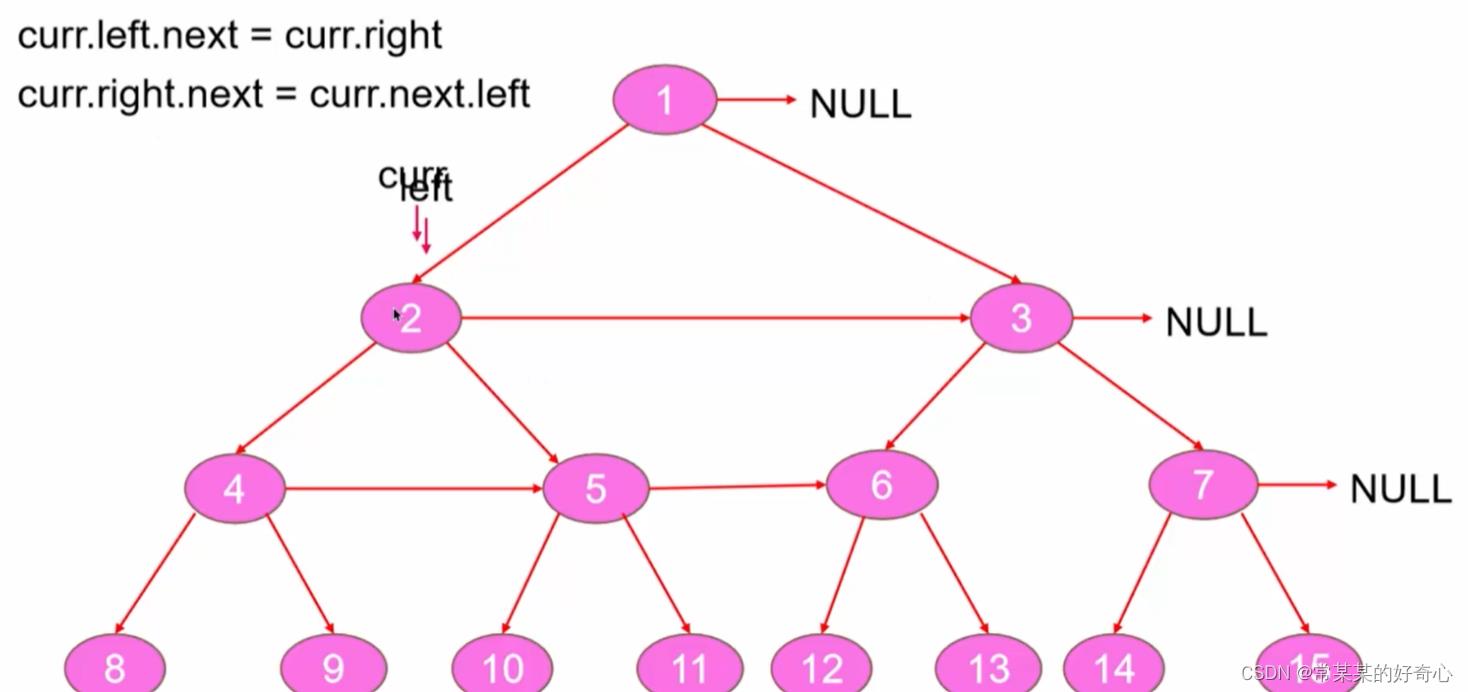
lc 116 :填充每个节点的下一个右侧节点指针
https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/
提示:
树中节点的数量在 [0, 2^12 - 1] 范围内
-1000 <= node.val <= 1000
进阶:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
#方案一:层序遍历
#o(n),o(n)
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:return None
queue=deque()
queue.append(root)
while queue:
size=len(queue)
for i in range(size):
curr=queue.popleft()
#对非最后节点的处理
if i != size - 1:
curr.next = queue[0] #key
if curr.left:queue.append(curr.left)
if curr.right: queue.append(curr.right)
return root
#方案二:双指针(进阶)
#o(1),o(n)
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:return None
#
left=root
curr=None
while left.left:
curr=left
#key
while curr:
curr.left.next=curr.right
if curr.next:
curr.right.next=curr.next.left
curr=curr.next
#
left=left.left
#
return root
#方案三:DFS(进阶)
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:return None
#
return self.dfs(root)
def dfs(self,node):
if not node:return None
#
left=node.left
right=node.right
#key
while left and right:
left.next=right
left=left.right
right=right.left
self.dfs(node.left)
self.dfs(node.right)
return node
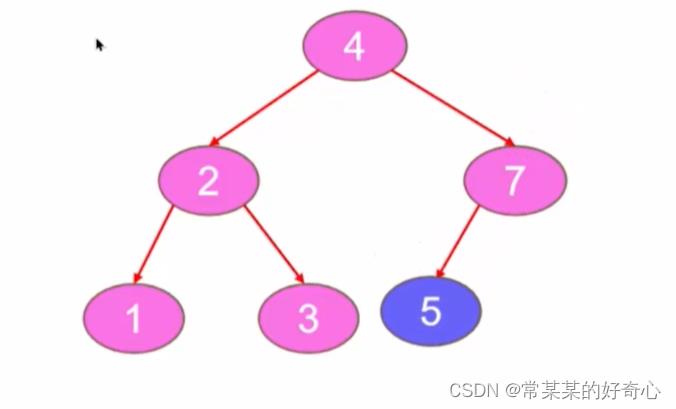
lc 701 :二叉搜索树中的插入操作
https://leetcode.cn/problems/insert-into-a-binary-search-tree/
提示:
树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。
#迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:return TreeNode(val)
#o(logn),o(1)
curr=root
while curr:
#
if val < curr.val:
#
if not curr.left:
curr.left=TreeNode(val)
return root
#
curr=curr.left
else:
if not curr.right:
curr.right=TreeNode(val)
return root
curr=curr.right
return root
#递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:return TreeNode(val)
#
if val <root.val:
root.left=self.insertIntoBST(root.left,val)
else:
root.right=self.insertIntoBST(root.right,val)
return root
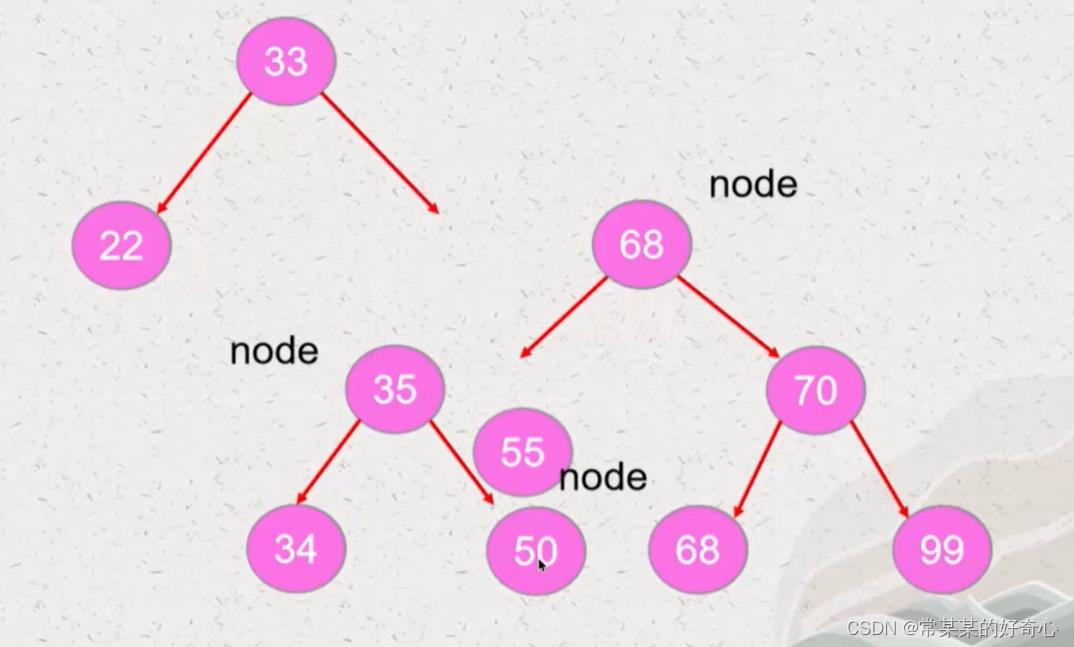
lc 108 :将有序数组转换为二叉搜索树
https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/
提示:
1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 按 严格递增 顺序排列
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
return self.build(nums,0,len(nums)-1)
def build(self,nums,left,right):
if left>right:return None
#
mid=left+(right-left)//2
root=TreeNode(nums[mid])
root.left=self.build(nums,left,mid-1)
root.right=self.build(nums,mid+1,right)
#
return root
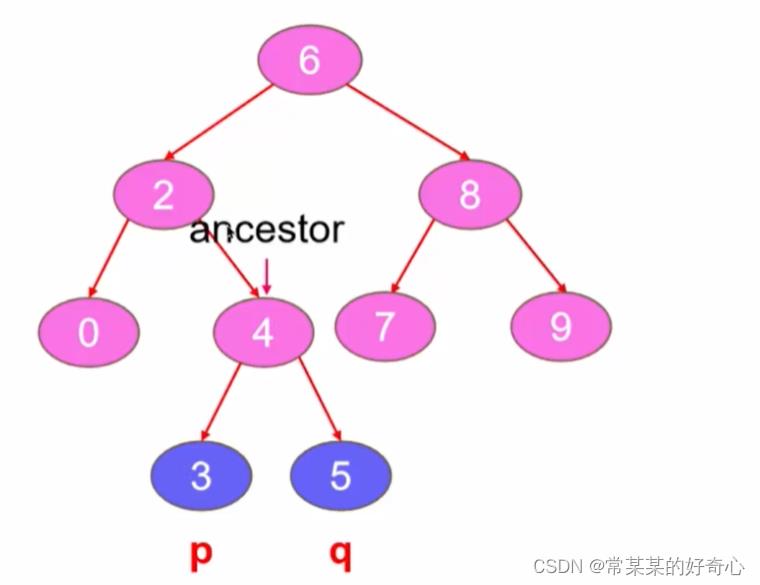
lc 235【剑指 68-1】 :二叉搜索树的最近公共祖先
https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
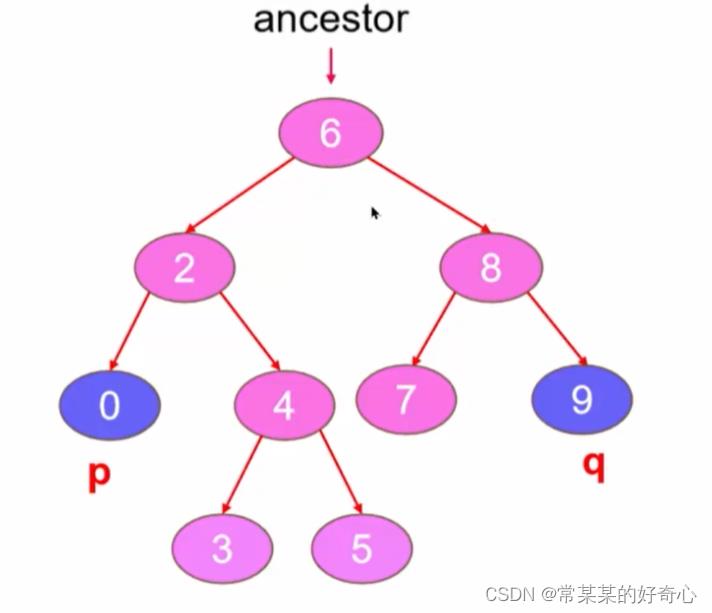
#类比LC-236
#利用BST的性质
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
#o(logn),o(1)
ancestor=root
while ancestor:
if p.val <ancestor.val and q.val<ancestor.val:
ancestor=ancestor.left
elif p.val > ancestor.val and q.val > ancestor.val:
ancestor=ancestor.right
else:
return ancestor
return ancestor
lc 98【top100】:验证二叉搜索树
https://leetcode.cn/problems/validate-binary-search-tree/
提示:
树中节点数目范围在[1, 10^4] 内
-2^31 <= Node.val <= 2^31 - 1
#方案一:中序遍历->res是否有序
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
self.isBST=True
self.prev=None
self.inorder(root)
return self.isBST
def inorder(self,node):
if not node:return None
#
self.inorder(node.left)
###key
if self.prev and self.prev.val >= node.val:
self.isBST=False
return
self.prev=node
self.inorder(node.right)
#方案二:后序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
return self.postorder(root,float('-inf'),float('inf'))
def postorder(self,node,lower,upper):
if not node:return True
#
if node.val<=lower or node.val>=upper:
return False
return self.postorder(node.left,lower,node.val) and self.postorder(node.right,node.val,upper)
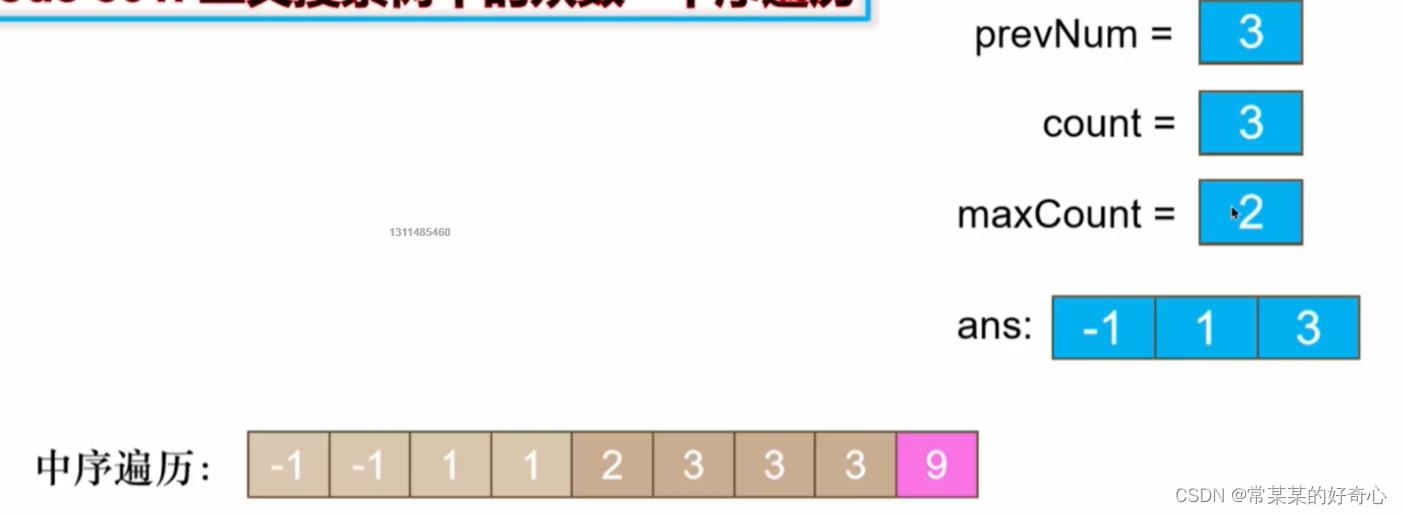
lc 501 :二叉搜索树中的众数
https://leetcode.cn/problems/find-mode-in-binary-search-tree/
提示:
树中节点的数目在范围 [1, 10^4] 内
-10^5 <= Node.val <= 10^5
进阶:
你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
#中序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findMode(self, root: Optional[TreeNode]) -> List[int]:
self.currnum=-1
self.count=0
self.maxcnt=0
self.res=[]
return self.dfs(root)
def dfs(self,node):
if not node:return
self.dfs(node.left)
self.update(node.val)
self.dfs(node.right)
return self.res
def update(self,val):
#计数
if self.currnum==val:
self.count+=1
else:
self.currnum=val
self.count=1
#统计
if self.count==self.maxcnt:
self.res.append(val)
elif self.count>self.maxcnt:
self.res=[val]
self.maxcnt=self.count
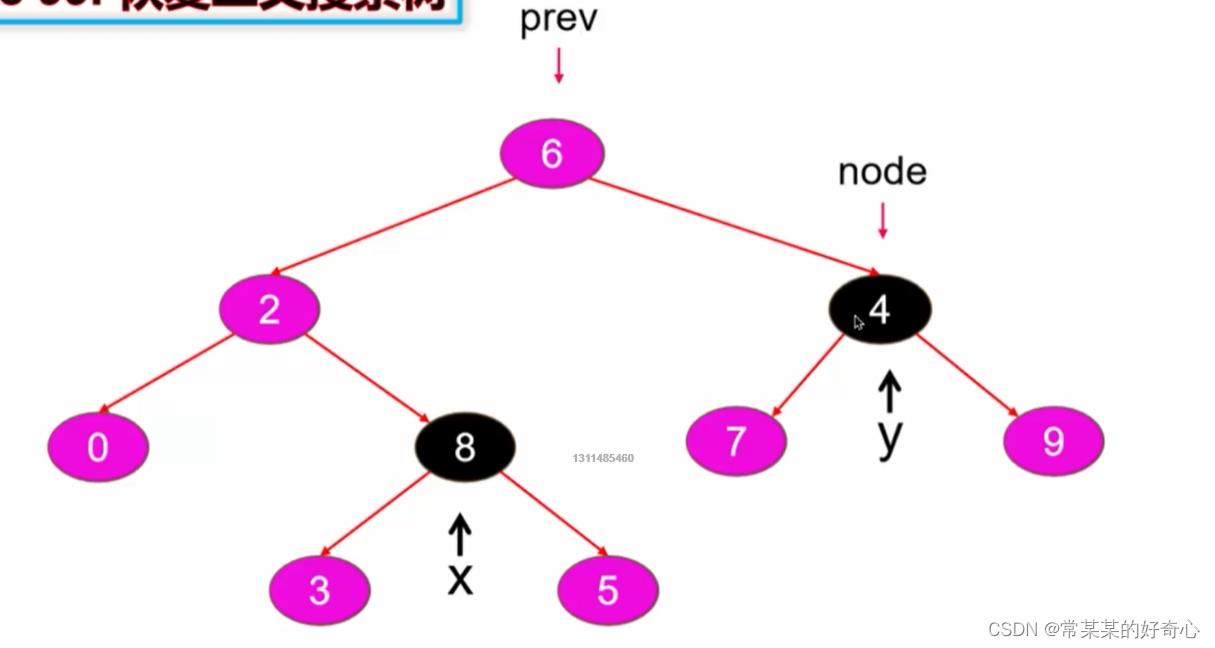
lc 99 :恢复二叉搜索树
https://leetcode.cn/problems/recover-binary-search-tree/
提示:
树上节点的数目在范围 [2, 1000] 内
-2^31 <= Node.val <= 2^31 - 1
进阶:
使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗?
#中序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def recoverTree(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
self.x=self.y=self.prev=None
self.dfs(root)
self.x.val,self.y.val以上是关于日常系列LeetCode《18·二叉树3》的主要内容,如果未能解决你的问题,请参考以下文章