人脑天生会算微积分，并应用于精准控制奔跑，来自MIT团队

Posted 2022-12-19 QbitAl

詹士 发自 凹非寺
量子位 | 公众号 QbitAI

What？你的大脑通过计算微积分来控制快速运动？

该发现来自MIT研究团队。

他们认为，大脑并非通过单一信号对高速运动精准控制，而是基于一套复杂的信号处理系统，对抑制、兴奋两种信号进行比对处理，得到最终指令。

论文中，研究团队还用一套更「形象」的说法描述该过程——大脑在自己算微积分。

目前，该项研究已发表在Cell Reports上。

一些网友看后颇感Amazing。

比如这位就表示，既然大脑都知道算微积分了，为啥大学还要学…….

还有这位，看过研究结论，表示：这岂不是很像PID控制器？

所以，科学家如何证明上述结论？

下面展开讲讲。

△ 图源：quantamagazine

发现大脑内的微积分系统

控制走路跑步的机制本身不难描述——大脑有个中脑运动区（MLR），它会向脊髓神经元发送信号。

信号后又流向腿部肌肉的运动神经元，这其中，兴奋、抑制两种信号分别直接控制了身体活动与停止。

但当奔跑有了目的地，事情变得复杂起来。

以前研究中，生物学家知道了目标信号是在大脑皮层形成，再传递给MLR。

但精准的指令如何下达？如何控制身体突然停下？这是个问题。

为此，研究者以小鼠为实验对象，开发一套实验系统。

他们将其小鼠头部固定，通过光遗传学设备控制神经元激活，同时让小鼠脚底踩着跑步机，给到特别的灯光图案地标，训练它移动。

若小鼠能走到地标处站住，并保持静止1.5s，就能听见奖励音并获得喂水，然后，继续去下一个指定位置。

反之，播送错误提示音不给喂水，重启任务。如此往复训练。

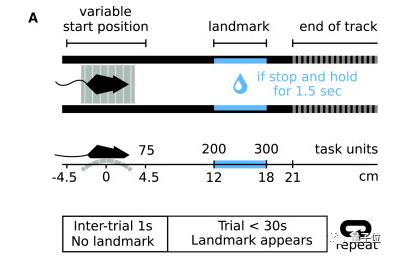
如果小鼠在30分钟内成功停留100次，研究者即开始研究其行为模式及信号传递过程。

他们首先观察了小鼠运动控制模式。

结果发现，小鼠为更快获得奖励，会先尽可能加速奔跑，然后在接近目标一定位置，快速刹车，以保证在正确位置停下。

科研者认为，此种现象证明了小鼠瞬间切换了自己的运动决策模式，并用一套方程描述该过程：

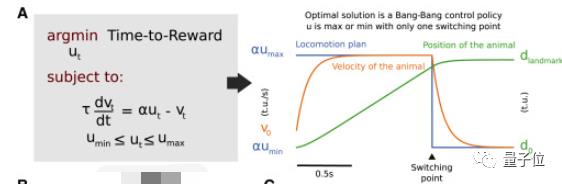
基于上面结论，结合之前理论研究，科研团队假设，大脑皮层的次级运动皮层（M2）到控制运动的中枢底丘脑核 (STN)，即M2-STN通路，所发信号，控制了动物运动的停止。

为此，他们向该通路输入信号，激活它。结果证实，小鼠奔向目标中，确实会提前停下，如下图A所示：

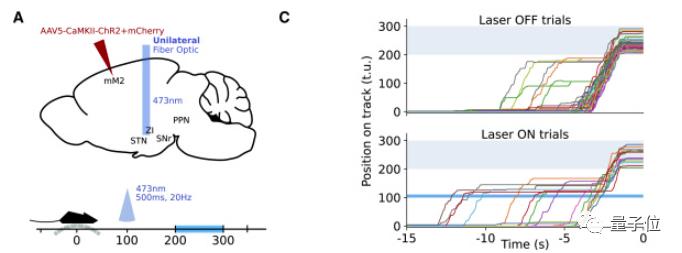
M2-STN通路虽能控制小鼠停下，但它是不是时刻都工作呢？

科研团队通过钙成像技术，观察该部分神经元活性的变化。

从中，他们能直接发现，在地标图案停止处，通路中神经元也同步出现停止信号。与之对应的，即便小鼠在途中停下，M2-STN通路停止信号却并未出现。

这说明了，该通路与小鼠奔向目的地任务直接相关，而与一般运动的停止活动无关，且由视觉输入信号主导系统变化。

更进一步，科学家将大脑各部分所监测到的活跃度随时间变化函数汇总，得到以下曲线：

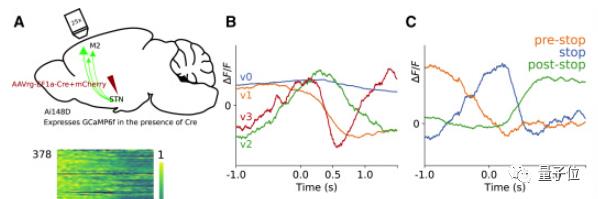
科研工作者将上述大脑各部分信号活跃函数汇总建模，给出一个对时间进行微分的反馈控制系统。

由次级运动皮层（M2）的视觉信号作为输入项。经过STN、MLR等部分，分成兴奋、抑制两路信号通过系统运算。

最终得到输出项，进而完成对动作的控制：

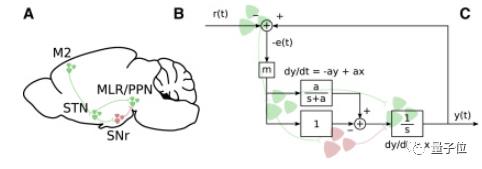
在构建系统中，研究者特别指出，由于脑内PPN部分连有多路神经元驱动运动，因此，系统对其进行了微分运算，来抵消随时间累积的积分运算影响。

科学家认为，正是基于上述系统，我们的身体能够短时间内快速根据输入信号切换运动模式，精准地在目的地到来前某个位置「开启减速刹车」，最终停在特定位置。

背后团队

最后认识一下研究团队。

本文通讯作者为Elie Adam与Mriganka Sur，均来自MIT的Picower 学习与记忆研究所。

Elie Adam博士专注于使用数学方法结合实验工程学来研究大脑动力学。

Mriganka Sur教授为此次研究背后团队主要负责人。

参考链接：
[1]https://doi.org/10.1016/j.celrep.2022.111139
[2]https://www.wired.com/story/your-brain-uses-calculus-to-control-fast-movements/
[3]https://www.quantamagazine.org/the-brain-uses-calculus-to-control-fast-movements-20221128/#comments