基于LS最小二乘法的无线定位matlab仿真

Posted 2022-12-15 fpga和matlab

up目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小 。最小二乘法还可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达 。
       最小二乘法还可用于曲线拟合。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。
选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小
       最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。

二、核心程序

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));

N=4;        %参与定位的基站数 
C=3e5;   %电磁波传播速度300000000m/s
X=[0 5000 5000 0];
Y=[0 0 5000 5000];
x=1200;    y=1600;
D(1:N)=sqrt((X(1:N)-x).^2+(Y(1:N)-y).^2);
delay(1:N)=D(1:N)./C;
T=1;
N_sample=200000;%传输速率200kbit/s
iTsignal=[ones(1,N_sample/2),-ones(1,N_sample/2)];%发送信号的实部
qTsignal=zeros(size(iTsignal));%发送信号的虚部
rsn=[0 3 5 10 20 30 40 50];  %信噪比
%rsn=40;
standard=0;       %1为b标准，0为a标准；
for j=1:8
    j
    for i=5
    [iRsignal1]=pathoutput(iTsignal,rsn(j),standard,delay(1));
    [iRsignal2]=pathoutput(iTsignal,rsn(j),standard,delay(2));
    [iRsignal3]=pathoutput(iTsignal,rsn(j),standard,delay(3));
    [iRsignal4]=pathoutput(iTsignal,rsn(j),standard,delay(4));
   
    iRsignal1(i,:)=iRsignal1;
    iRsignal2(i,:)=iRsignal2;
    iRsignal3(i,:)=iRsignal3;
    iRsignal4(i,:)=iRsignal4;
    
    end
    iRsignal1=mean(iRsignal1);
    iRsignal2=mean(iRsignal2);
    iRsignal3=mean(iRsignal3);
    iRsignal4=mean(iRsignal4);
   
   TDOA(1)=correlation(iRsignal2,iRsignal1,T,N_sample);
   TDOA(2)=correlation(iRsignal3,iRsignal1,T,N_sample);
   TDOA(3)=correlation(iRsignal4,iRsignal1,T,N_sample);
   
   Q=eye(N-1);
   for i=1:N-1
    Rplus(i)=TDOA(i)*C; %第一个reader为主站其余为辅站，Ri,1为第i个站到定位点的距离与第一个站到其距离的差。
    R(i)=(TDOA(i)*C).^2; %为了在Tdoainiial函数中使用R
   end                                                                           %Q=sigma(l).*[1 0.5 0.5;0.5 1 0.5;0.5 0.5 1]; %噪声协方差阵随着基站的数目变化而改变。
   [xu yu]=Leastsquare(X,Y,N,Q,R,Rplus,x,y);
    xr(j)=xu-x;
    yr(j)=yu-y;
    locationerror(j)=sqrt((xu-x).^2+(yu-y).^2);
end

三、测试结果

 

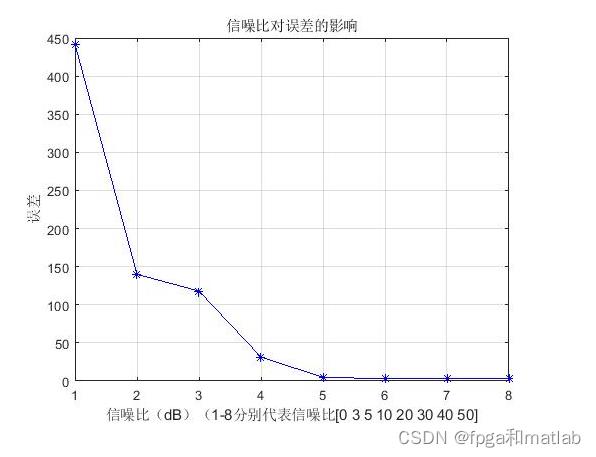
up17