Keras深度学习实战（39）——音乐音频分类

Posted 2022-12-15 盼小辉丶

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Keras深度学习实战（39）——音乐音频分类相关的知识，希望对你有一定的参考价值。

Keras深度学习实战（39）——音乐音频分类

0. 前言

音乐音频分类技术能够基于音乐内容为音乐添加类别标签,在音乐资源的高效组织、检索和推荐等相关方面的研究和应用具有重要意义。传统的音乐分类方法大量使用了人工设计的声学特征，特征的设计需要音乐领域的知识，不同分类任务的特征往往并不通用。深度学习的出现给更好地解决音乐分类问题提供了新的思路，本文对基于深度学习的音乐音频分类方法进行了研究。首先将音乐的音频信号转换成声谱作为统一表示，避免了手工选取特征存在的问题，然后基于一维卷积构建了一种音乐分类模型。

1. 数据集与模型分析

在本节中，我们将研究对音乐音频进行分类，当我们能够使用深度学习模型对歌曲类型自动分类时，可以极大程度的减少人工成本。

1.1 数据集分析

在我们使用数据集中包含 10 种可能的流派类型，包括 blues、classical、country、disco、hiphop、jazz、metal、pop、reggae 和 rock。并且每类音乐包含 100 首歌曲，因此数据集中共有 1000 首歌曲，歌曲的文件夹名即为歌曲的类型：

相关数据集可以在以下链接中下载：https://pan.baidu.com/s/1quERojOMz2j2_JyBhOkCwg，xqih。

1.2 模型分析

在我们将采用如下策略对歌曲进行分类：

下载数据集，其中包含音频文件及其流派类型信息
可视化并对比各种类型的音频文件的频谱图
对音频文件的频谱图上执行一维卷积操作
经过多次卷积和池化操作后，从卷积神经网络中提取音频特征
展平卷积神经网络输出，并将其输入到具有 10 个节点的全连接层中，表示 10 种可能的类别
最小化分类交叉熵损失，以将音频文件分类为 10 种可能的类别之一

对音频进行分类后，可视化每个音频输入的嵌入，以便将相似的音频文件进行分组。这样，我们能够在无需收听新歌曲的情况下识别其流派，从而自动对音频文件进行分类。

2. 歌曲流派分类模型

接下来，我们将使用 Keras 实现上一小节中所讨论的分类模型。

2.1 数据加载与预处理

(1) 首先，下载数据集并导入相关的库：

import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt
import os
import librosa
import librosa.display

from keras.models import Model
from keras.layers import Input, Dense, Dropout
from keras.layers import Conv1D, MaxPooling1D, GlobalMaxPooling1D
from keras.layers import BatchNormalization

import numpy as np
from sklearn.model_selection import train_test_split
import keras

(1) 循环浏览音频文件以提取输入音频的梅尔频谱图输入特征，并存储音频输入的流派信息作为模型目标输出：

song_specs = []
genres = []

genres_folder = 'genres'

for genre in os.listdir(genres_folder):
    song_folder = os.path.join(genres_folder, genre)
    # print(song_folder)
    for song in os.listdir(song_folder):
        if song.endswith('.au'):
            signal, sr = librosa.load(os.path.join(song_folder, song), sr=16000)
            melspec = librosa.feature.melspectrogram(y=signal, sr=sr).T[:1280,]
            song_specs.append(melspec)
            genres.append(genre)
            # print(song)
    print("Done with: ", genre)

在以上代码中，我们加载音频文件并提取其特征，提取信号的质谱图特征，最后，将梅尔特征存储为输入数组，将音乐的流派存储为输出数组。

(2) 可视化音频文件的频谱图，可以看到古典音频频谱图和摇滚音频频谱图之间存在明显的区别：

plt.subplot(121)
librosa.display.specshow(librosa.power_to_db(song_specs[305].T), y_axis='mel', x_axis='time')
plt.title('Classical audio spectrogram')
plt.subplot(122)
librosa.display.specshow(librosa.power_to_db(song_specs[405].T), y_axis='mel', x_axis='time',)
plt.title('Rock audio spectrogram')
plt.show()

(3) 定义输入和输出数组，并将输出类别转换为独热编码：

song_specs = np.array(song_specs)
song_specs2 = []
for i in range(len(song_specs)):
    tmp = song_specs[i]
    song_specs2.append(tmp[:900][:])

song_specs2 = np.array(song_specs2)
genre_one_hot = pd.get_dummies(genres)

(4) 将数据集拆分为，训练和测试数据集：

x_train, x_test, y_train, y_test = train_test_split(song_specs2, np.array(genre_one_hot),test_size=0.1)
print(x_train.shape)

2.2 模型构建与训练

(1) 构建模型，并进行编译：

input_shape = (900, 128)
inputs = Input(input_shape)
x = inputs
levels = 64
for level in range(7):
    x = Conv1D(levels, 3, activation='relu')(x)
    x = BatchNormalization()(x)
    x = MaxPooling1D(pool_size=2, strides=2)(x)
    levels *= 2
x = GlobalMaxPooling1D()(x)

for fc in range(2):
    x = Dense(256, activation='relu')(x)
    x = Dropout(0.5)(x)
labels = Dense(10, activation='softmax')(x)

model = Model(inputs=[inputs], outputs=[labels])
print(model.summary())
adam = keras.optimizers.Adam(lr=0.0001)
model.compile(loss='categorical_crossentropy',optimizer=adam,metrics=['acc'])

以上代码中的 Conv1D 网络层的计算原理与 Conv2D 非常相似。但是，在 Conv1D 中使用的是一维卷积核，而在 Conv2D 中使用的是二维卷积核。模型的简要架构信息如下所示：

Model: "functional_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         [(None, 900, 128)]        0         
_________________________________________________________________
conv1d (Conv1D)              (None, 898, 64)           24640     
_________________________________________________________________
batch_normalization (BatchNo (None, 898, 64)           256       
_________________________________________________________________
max_pooling1d (MaxPooling1D) (None, 449, 64)           0         
_________________________________________________________________
conv1d_1 (Conv1D)            (None, 447, 128)          24704     
_________________________________________________________________
batch_normalization_1 (Batch (None, 447, 128)          512       
_________________________________________________________________
max_pooling1d_1 (MaxPooling1 (None, 223, 128)          0         
_________________________________________________________________
conv1d_2 (Conv1D)            (None, 221, 256)          98560     
_________________________________________________________________
batch_normalization_2 (Batch (None, 221, 256)          1024      
_________________________________________________________________
max_pooling1d_2 (MaxPooling1 (None, 110, 256)          0         
_________________________________________________________________
conv1d_3 (Conv1D)            (None, 108, 512)          393728    
_________________________________________________________________
batch_normalization_3 (Batch (None, 108, 512)          2048      
_________________________________________________________________
max_pooling1d_3 (MaxPooling1 (None, 54, 512)           0         
_________________________________________________________________
conv1d_4 (Conv1D)            (None, 52, 1024)          1573888   
_________________________________________________________________
batch_normalization_4 (Batch (None, 52, 1024)          4096      
_________________________________________________________________
max_pooling1d_4 (MaxPooling1 (None, 26, 1024)          0         
_________________________________________________________________
conv1d_5 (Conv1D)            (None, 24, 2048)          6293504   
_________________________________________________________________
batch_normalization_5 (Batch (None, 24, 2048)          8192      
_________________________________________________________________
max_pooling1d_5 (MaxPooling1 (None, 12, 2048)          0         
_________________________________________________________________
conv1d_6 (Conv1D)            (None, 10, 4096)          25169920  
_________________________________________________________________
batch_normalization_6 (Batch (None, 10, 4096)          16384     
_________________________________________________________________
max_pooling1d_6 (MaxPooling1 (None, 5, 4096)           0         
_________________________________________________________________
global_max_pooling1d (Global (None, 4096)              0         
_________________________________________________________________
dense (Dense)                (None, 256)               1048832   
_________________________________________________________________
dropout (Dropout)            (None, 256)               0         
_________________________________________________________________
dense_1 (Dense)              (None, 256)               65792     
_________________________________________________________________
dropout_1 (Dropout)          (None, 256)               0         
_________________________________________________________________
dense_2 (Dense)              (None, 10)                2570      
=================================================================
Total params: 34,728,650
Trainable params: 34,712,394
Non-trainable params: 16,256
_________________________________________________________________

(2) 拟合模型：

history = model.fit(x_train, y_train,
                    batch_size=64,
                    epochs=200,
                    verbose=1,
                    validation_data=(x_test, y_test))

训练完成后，我们可以看到模型在测试数据集上的分类准确率大约为 65％：

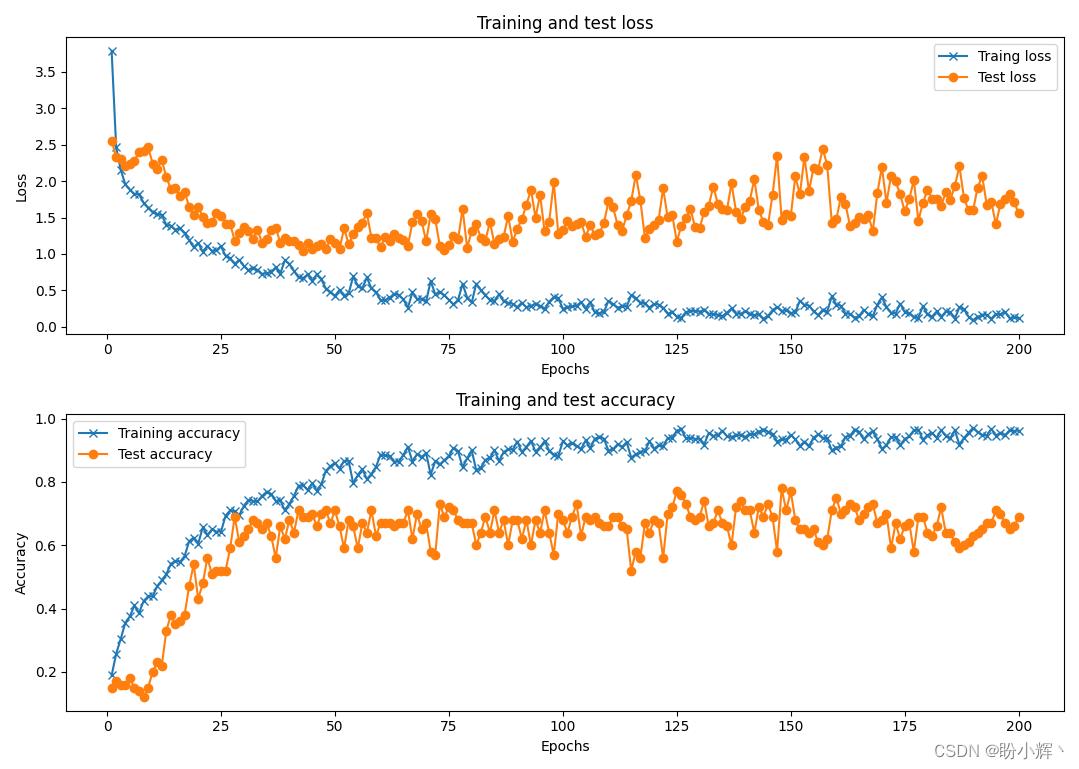
3. 聚类分析

(1) 为了对歌曲进行聚类分析，我们提取模型输出，具体而言，提取倒数第二个全连接层的输出：

layer_name = 'dense_1'
intermediate_layer_model = Model(inputs=model.input,outputs=model.get_layer(layer_name).output)
intermediate_output = intermediate_layer_model.predict(song_specs2)

(2) 使用 t-SNE 将嵌入的尺寸减小到 2，以便可以方便的进行可视化：

from sklearn.manifold import TSNE
tsne_model = TSNE(n_components=2, verbose=1, random_state=0)
tsne_img_label = tsne_model.fit_transform(intermediate_output)
tsne_df = pd.DataFrame(tsne_img_label, columns=['x', 'y'])
genre_one = np.argmax(np.array(genre_one_hot), axis=1)
tsne_df['song_label'] = genre_one.tolist()

(3) 最后，绘制 t-SNE 输出：

from matplotlib.colors import ListedColormap

colors = ListedColormap(['#EE7C6B', '#EC870E', '#C7C300', '#489620', '#008C5E', '#00B2BF', '#184785', '#3A2885', '#52096C', '#A2007C'])
values = [label for label in tsne_df['song_label']]
classes = []
for label in genres:
    if label not in classes:
        classes.append(label)
scatter=plt.scatter(tsne_df['x'], tsne_df['y'], c=values, cmap=colors)
plt.legend(handles=scatter.legend_elements()[0], labels=classes)
plt.show()

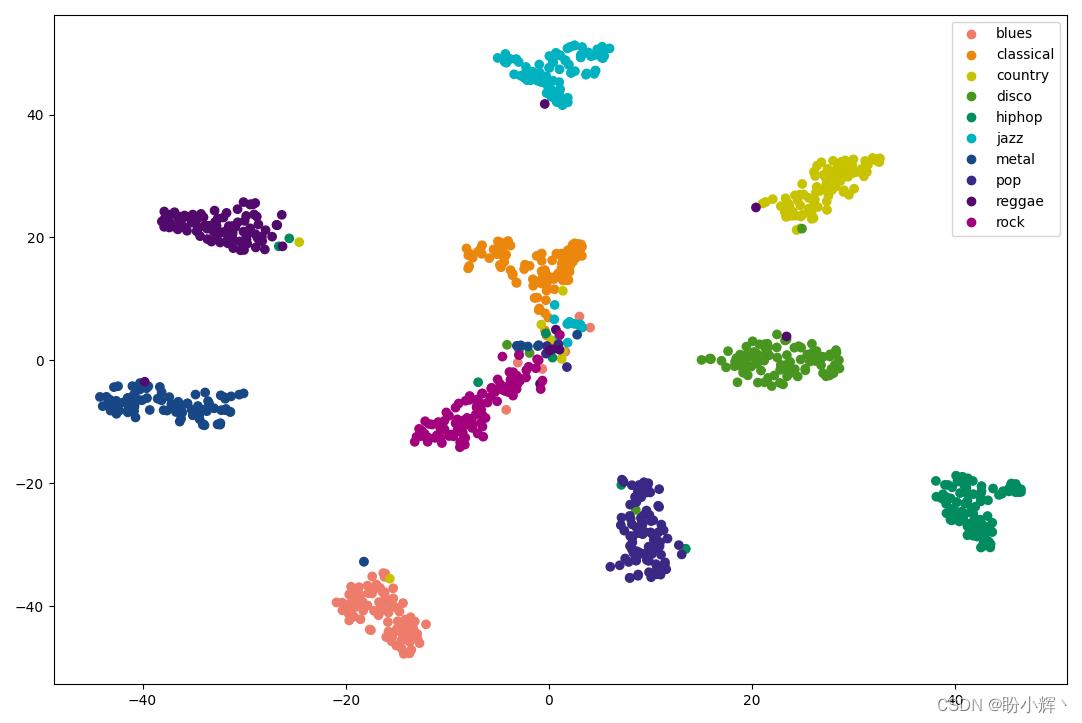
从上图可以看出，类似流派的音频文件被聚类在一起。这样，我们就可以以较高的准确率自动地将新歌分类为可能的流派，而无需人工检查。但是，如果音频属于某种流派的置信度较低，则有可能需要进行人工检查，以进一步降低误分类率。

小结

音乐音频分类技术能够基于音乐内容为音乐添加类别标签,在音乐资源的高效组织、检索和推荐等相关方面的研究和应用具有重要意义。本文对基于深度学习的音乐音频分类方法进行了研究，基于一维卷积构建了音乐分类模型，对音乐流派的大部分标签具有良好的标注能力，所设计的音乐分类方法实现了一个基于音频的音乐标签标注系统，为构建音乐领域知识图谱提供了数据支持。

系列链接

以上是关于Keras深度学习实战（39）——音乐音频分类的主要内容，如果未能解决你的问题，请参考以下文章

Keras深度学习实战（10）——音频分类

AI 音辨世界：艺术小白的我，靠这个AI模型，速识音乐流派选择音乐 ⛵

Keras深度学习实战（40）——音频生成

Keras深度学习实战（19）——使用对抗攻击生成可欺骗神经网络的图像

Keras深度学习实战——基于ResNet模型实现性别分类

Keras深度学习实战——新闻文本分类