二叉搜索树

Posted 2022-12-15 --Allen--

红黑树不仅是二叉树，也是二叉搜索树。如果你想学习红黑树，却不了解二叉搜索树的性质，这就是典型的爬还没学会就想学走。所以本文就来讨论二叉搜索树的一点简单的性质以及操作。

在此之前，你需要下载这份代码(C++)，并对照实现：https://github.com/ivanallen/dsa

1. 性质

二叉树中：

• 对于任意一个节点，左孩子的值都它的值小，右孩子的值比它的值大（或等于）。（二叉搜索树一定满足这个性质，但是满足这个条件不一定是二叉搜索树。）
• 对于任意一个节点，左子树所有节点的值比它的值小，右子树所有的节点的值比它大（或等于）。

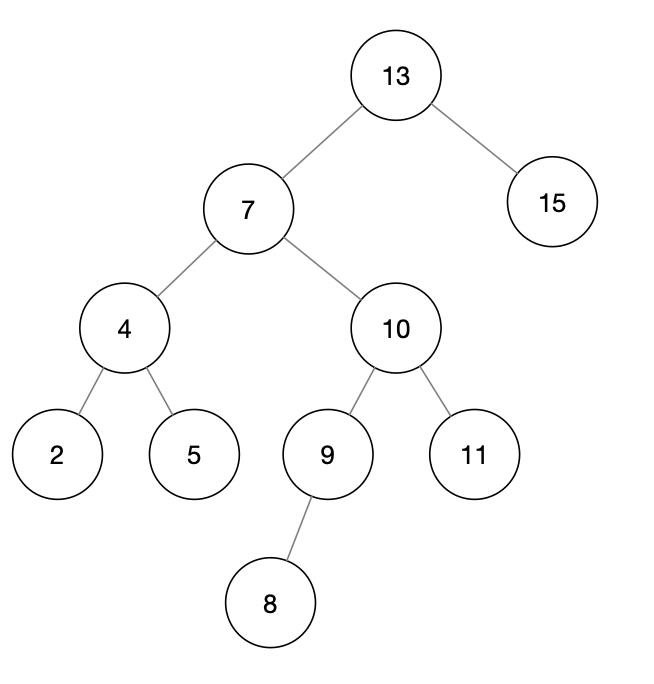
图 1 就是一棵二叉搜索树：

图 1 二叉搜索树

2. 操作

javascript 具有极强的表达能力，因此这里选择 javascript 作为伪代码描述算法。使用伪代码描述算法的好处非常多，它能使你摆脱语言上的细节，把精力放到算法本身，而不是语言上。

为了简化思考，在代码中会出现 x, y, z 这些表示节点变量，我们约定：

• x 表示当前节点
• y 表示当前节点的父节点，即 x 的父亲是 y
• z 表示新节点或要被移除的节点

// 表示二叉树
let tree = 
	root: null
;

// 表示节点
let node = 
	left: null,   // 左孩子
	right: null,  // 右孩子
	parent: null, // 父节点
	key: 0
;

2.1 查找

function search(tree, key) 
	return _search(tree.root, key);


function _search(x, key) 
	if (x == null || x.key = key) 
		return x;
	
	if (key < x.key) 
		return _search(x.left, key);
	 else 
		return _search(x.right, key);
	

下面是迭代版本的查找算法：

function iterative_search(tree, key) 
	let x = tree.root;
	while(x != null) 
		if (x.key == key) 
			break;
		 else if (key < x.key) 
			x = x.left;
		 else 
			x = x.right;
		
	
	return x;

2.2 插入

插入算法需要讨论两种情况：

• 空树
• 非空树

function insert(tree, z) 
	if (tree.root == null) 
		tree.root = z;
		return;
	

	let x = tree.root;
	let y = null;
	while(x != null) 
		y = x; // y 始终是 x 的父亲节点。
		if (z.key < x.key) 
			x = x.left;
		 else 
			x = x.right;
		
	
	if (z.key < y.key) 
		y.left = z;
	 else 
		y.right = z;
	
	z->parent = y;

2.3 删除

二叉树的删除比较复杂，需要分成三种情况：

• 情况一：被删除的节点是叶子节点
• 情况二：被删除的节点只有一个左孩子(或右孩子)
• 情况三：被删除的节点既有左孩子和右孩子

另外，我们需要一些基础函数：

• transplant(tree, u, v) : 节点移植，用 v 替换掉 u, 并返回 u.
• successor(x) : 查 x 后继

分析：如果我们把 null 节点也视作特殊的“孩子"，情况一和二，可以合并成一类处理。最复杂的是情况三，但是，情况三可以转换成情况一和情况二，这是算法处理中非常常见的手段，即把未知问题转换为已知问题。

情况一和二，如果要删除的节点 z 的左孩子是空，则用右孩子替换掉 z，即 transplant(z, z.right)，反之则 transplant(z, z.left).

情况三的转换方式非常简单，如果要删除的节点 z，同时拥有左右孩子，只需要把 z 的前驱节点或者后继节点替换掉 z 即可。在本文中，我们选择使用后继 s 来替换掉 z. 例如下图 2，要删除节点 6，我们只要找到 6 的后继 7，并用 7 代替 6 即可。

图2 删除节点6

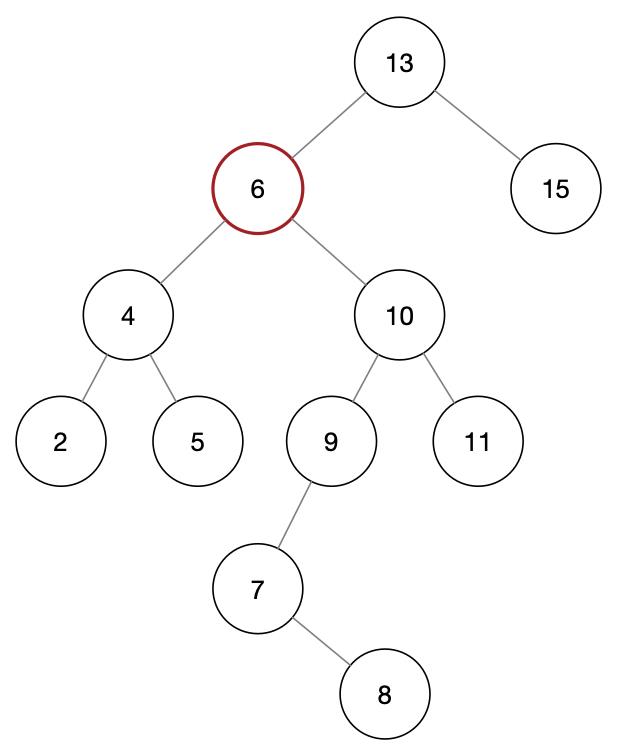
在情况三中，作为 z 的后继 s，它一定没有左孩子，就像上面中和后继节点 7，没有左孩子。要想使用 7 替换 6，首先我们得把 7 从树中删除，而这个删除操作，就是最简单的情况二了。删除掉 7 后，再把 6 的右子树挂到 7 的右侧，最后执行 transplant 操作。

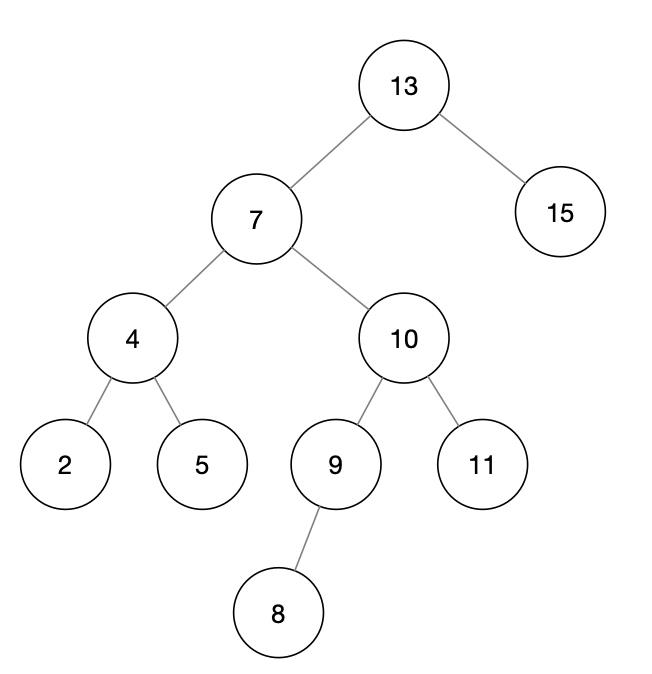
图 3 中，是删除掉 6 后的树：

图3 删除6后的树

• remove 删除节点

function remove(tree, z) 
	if (z == null) return;

	if (z.left == null) 
		transplant(tree, z, z.right);
	 else (z.right == null) 
		transplant(tree, z, z.left);
	 else 
		// 1. 查 z 后继 s, s 节点一定没有左孩子
		let s = successor(z);
		// 2. 将 s 从树中移除（转换成了情况二）
		remove(tree, s);
		// 3. 把 z 的右子树挂到 s 的右侧
		s.right = z.right;
		z.right.parent = s;
		// 4. 用 s 替换掉 z
		transplant(tree, z, s);
		// 5. 将 z 的左孩子挂到 s 的左侧
		s.left = z.left;
		z.left.parent = s;
	

• transplant 移植

function transplant(tree, u, v) 
	if (u == tree.root) 
		tree.root = v;
	 else if (u == u.parent.left) 
		u.parent.left = v;
	 else if (u == u.parent.right) 
		u.parent.right = v;
	
	return u;

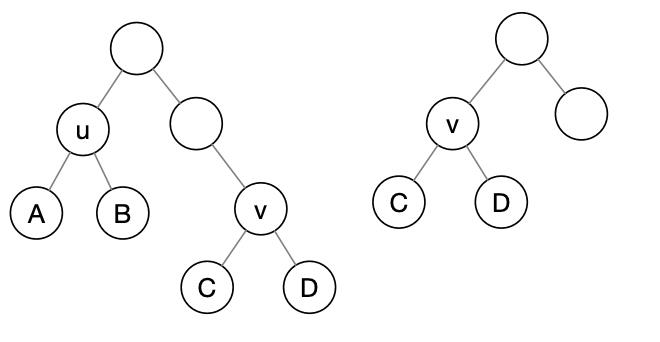
下图是 transplant 过程：

图4 transplant(u, v) 操作

• successor 查后继

function successor(x) 
	if (x->right != null) 
		let y = null;
		while (x != null) 
			y = x;
			x = x.left;
		
		return y;
	 else 
		let y = x.parent;
		while(y != null && y.right == x) 
			x = y;
			y = x.p;
		
		return y;
	

• 删除节点 z 的过程
  

图5 删除节点z(一)

图6 删除节点z(二)

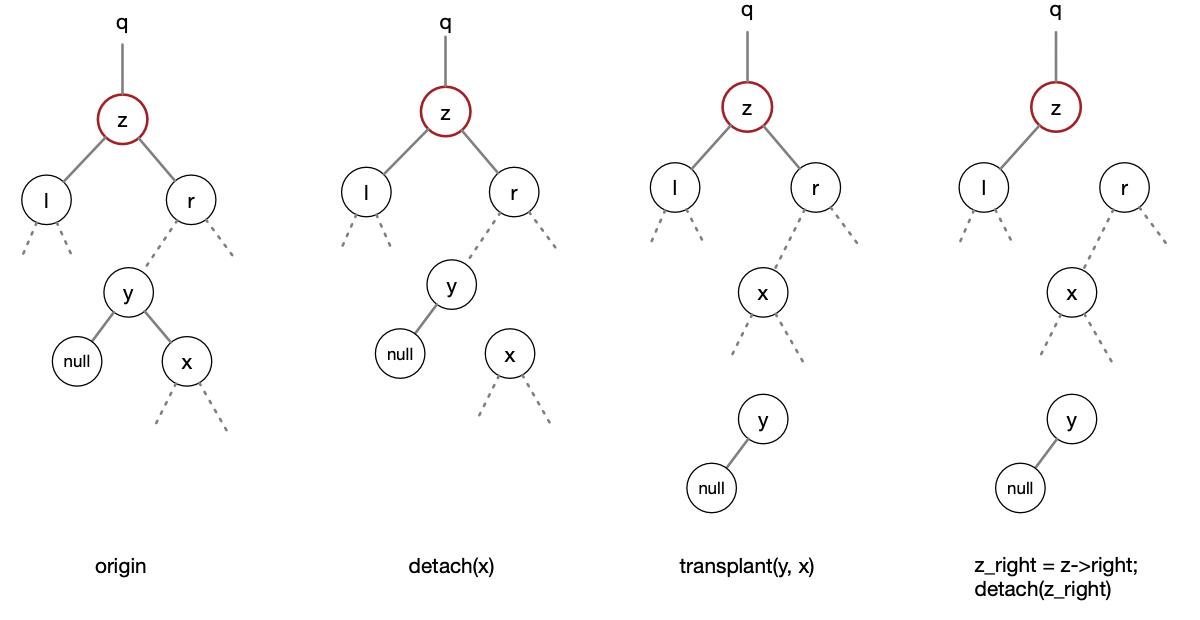
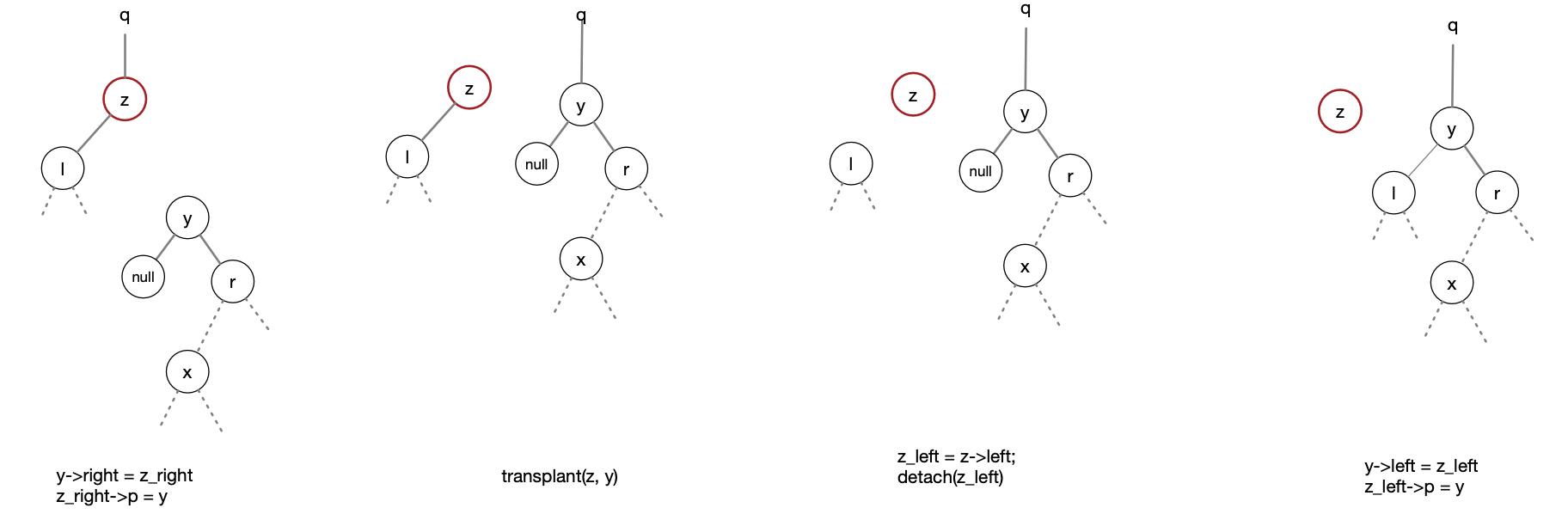
3. 总结

• 掌握二叉搜索树的插入、删除和搜索。

思考：successor 算法原理是什么？