DFS剪枝数独（简单版）

Posted 2022-12-14 行码棋

题目链接：

https://www.acwing.com/problem/content/168/

---

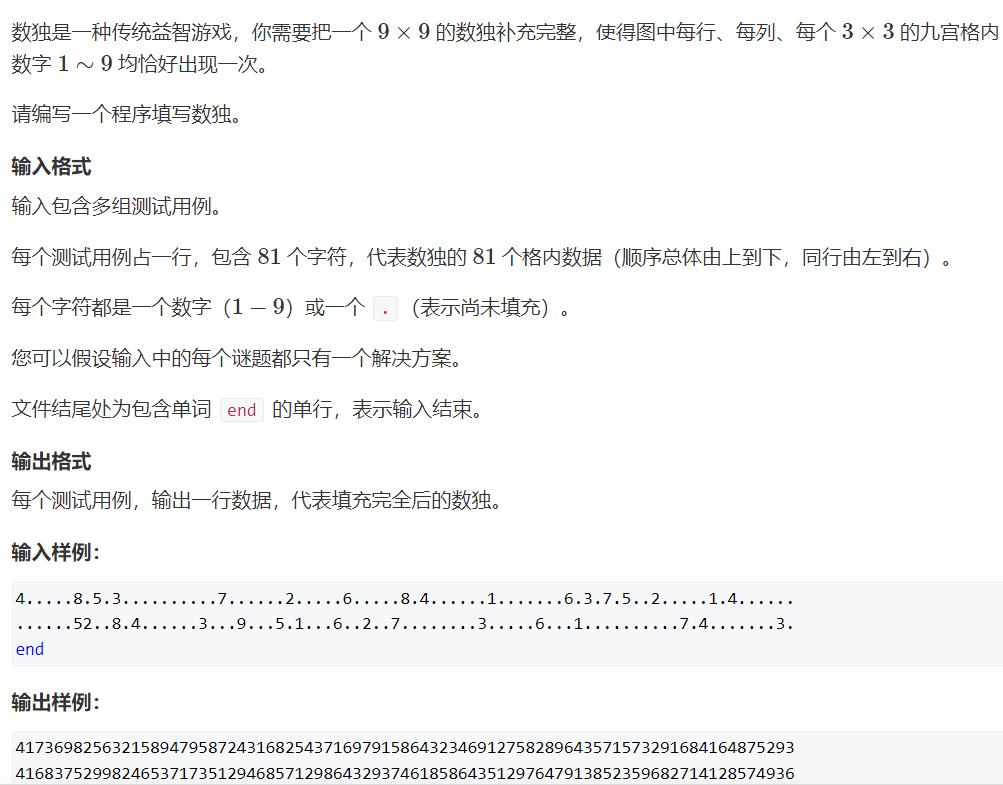
搜索以及剪枝策略：

• 搜索顺序优化： 首先搜索可填最少数量数字的格子
• 二进制优化：用两个数组row[], col[]存储每一行和每一列的可以填的数的状态，一共9位二进制，该位为1时代表可以选，为0时代表不可以选。
• lowbit优化：取每一位可以选的数时采用的操作

代码解释：
mn：就是单元格中求 最小的可以填的个数
ones[i]：i二进制中1的个数
dfs(cnt):代表从可以填cnt个数开始搜索

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 9;

int ones[1 << N], mp[1 << N];
int row[N], col[N], cell[3][3];
char s[100];
// 获取可以填的数的二进制状态
int get(int x, int y)

	return row[x] & col[y] & cell[x / 3][y / 3];

bool dfs(int cnt)

	if(!cnt) return true;

	int mn = 10;
	int x, y;
	for(int i = 0; i < N; i++)
		for(int j = 0; j < N; j++)
		
			if(s[i * N + j] == '.')
			
				int t = ones[get(i, j)];
				if(t < mn)
				
					mn = t;
					x = i, y = j;
				
			
		

	for(int i = get(x, y); i; i -= i & (-i))
	
		int t = mp[i & (-i)];
		row[x] -= 1 << t;
		col[y] -= 1 << t;
		cell[x / 3][y / 3] -= 1 << t;

		s[x * N + y] = '1' + t;

		if(dfs(cnt - 1)) return true;

		row[x] += 1 << t;
		col[y] += 1 << t;
		cell[x / 3][y / 3] += 1 << t;

		s[x * N + y] = '.';
	
	return false;

int main()

	ios::sync_with_stdio(false);
	cin.tie(0);

	for(int i = 0; i < N; i++) 
		mp[1 << i] = i;
	for(int i = 0; i < 1 << N; i++)
	
		int cnt = 0;
		for(int j = i; j; j -= j & (-j)) 
			cnt++;
		ones[i] = cnt;
	


	while(cin >> s, s[0] != 'e')
	
		for(int i = 0; i < N; i++)
			row[i] = col[i] = (1 << N) - 1;
		for(int i = 0; i < 3; i++)
			for(int j = 0; j < 3; j++)
				cell[i][j] = (1 << N) - 1;

		int cnt = 0;
		for(int i = 0, k = 0; i < N; i++)
			for(int j = 0; j < N; j++, k++)
			
				if(s[k] != '.')
				
					int t = s[k] - '1';
					row[i] -= (1 << t);
					col[j] -= (1 << t);
					cell[i / 3][j / 3] -= (1 << t);
				
				else cnt++;
			

		dfs(cnt);
		cout << s << "\\n";
	
 	return 0;