Applied Nonparametric Statistics-lec8
Posted pxy7896
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Applied Nonparametric Statistics-lec8相关的知识,希望对你有一定的参考价值。
Ref:https://onlinecourses.science.psu.edu/stat464/print/book/export/html/11
additive model
value = typical value + row effect + column effect + residual
predicate value = typical value + row effect + column effect
其中value是我们关注的值,typical value是overall median,row effect是block effect,column effect是treatment effect
下面用例题来展示:
问题:对于面包中烟酸(维生素B3)的含量,三个实验室(abc)的测量方法可能不同。烟酸的含量分为三档:
no niacin、2mg/100gm、4mg/100gm。我们把一些样本送到三个实验室做检测,希望知道:划分档次时,是否
基于烟酸的实际含量。
输入:niacin_r.txt(参见网页)
步骤一:
Plots the mean (or other summary) of the response for two-way combinations of factors, thereby illustrating possible interactions.
data = read.table("niacin_r.txt", header=F, sep=",")
data = as.data.frame(data)
names(data)=c("niacin", "lab", "level")
attach(data)
interaction.plot(lab, level, niacin, fun=median)
detach(data)
结果如图
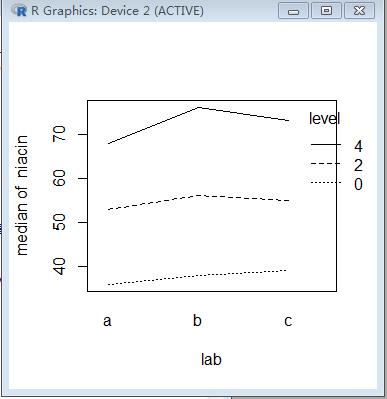
因为三条线基本是平行的(没有明显的交叉),所以我们可以继续做。(additive model没有考虑interaction的情况)
现在需要整理一下数据:首先将数据按照lab和level聚集一下
a=aggregate(niacin~lab+level, data=data, median)
结果是这样的:
> a lab level niacin 1 a 0 36 2 b 0 38 3 c 0 39 4 a 2 53 5 b 2 56 6 c 2 55 7 a 4 68 8 b 4 76 9 c 4 73
然后将它变成矩阵,每一行表示block(这里是level水平,0,2,4),每一列表示treat(这里是lab,abc)
> m=matrix(a[,3], nrow=3, ncol=3, byrow=T)
> m
[,1] [,2] [,3]
[1,] 36 38 39
[2,] 53 56 55
[3,] 68 76 73
步骤二:median polish
> medpolish(m)
1: 7
Final: 7
Median Polish Results (Dataset: "m")
Overall: 55
Row Effects:
[1] -17 0 18
Column Effects:
[1] -2 1 0
Residuals:
[,1] [,2] [,3]
[1,] 0 -1 1
[2,] 0 0 0
[3,] -3 2 0
这样我们已经得到了完整的additive model,其中typical value即overall,也就是55。
注意:medpolish实际是将前面的结果做了一个拆分,比如
m[1,1] = 36 = overall + column_effect[1] + row_effect[1] + residuals[1, 1] = 55 + (-17) + (-2) + 0
为了确定模型的好坏,我们计算统计量R*。如上例,TV是55,计算出R*约为0.9346,也就是说,考虑了lab和level的这种
additive model,可以解释93%的烟酸水平评定结果。
(the additive model of the labs and levels of niacin explain about 93% of the variation in the measured niacin levels.)

如果三条线有交叉,就要对每个block(每行)分别进行考虑,使用kruskal test。如果overall error rate是0.09,3个block的话,
那么每个的α值就是0.03(p值小于它就拒绝原假设)。
判断interaction的统计量可以用上面得到的Residuals矩阵,使用Q这个统计量,使用自由度为(b-1)×(k-1)的卡方分布决定p值
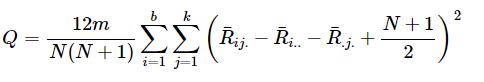
Dichotomous Data (Cochran\'s Tests)
b个block,k个treatment,实际数值只有两种,即0和1
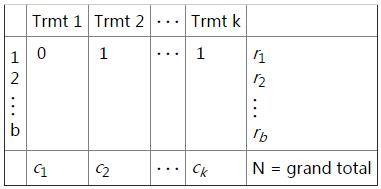
前提:blocks是随机选择的;结果变量是二值化的。
假设:
H0:treatments are equally effective
H1:difference in effectiveness among treatments.
以上是关于Applied Nonparametric Statistics-lec8的主要内容,如果未能解决你的问题,请参考以下文章