图像聚类-谱聚类

Posted 2022-12-13 小胖子小胖子

最近做的一个东西跟这个相关，本来希望是用深度学习对于没有标签的图像数据进行分类，但是通常情况下，深度学习是对有标签的数据进行学习，目的是用来自动提取特征，代替传统的手工提取特征。因此，比较容易想到，对于无标签又需要分类的图像数据，可以尝试先采用聚类来解决.

 

下面的内容是译自Jan Erik Solem的《Programming Computer Vision with Python》的第6章，该书已经由朱文涛和袁勇学长对该书进行了翻译，主要涉及相关代码和实例，可以转至http://yongyuan.name/pcvwithpython/。我仅对其中第6章的理论进行翻译，中途穿插自己的理解。

 

该博文仅供交流学习，如有侵权，请联系删除。

===================================================================================

（接上）

6.3 谱聚类

聚类算法的一个有趣的类型叫做谱聚类。谱聚类相对K均值和层次聚类来说有不同的方法。

对于n个元素的相似度矩阵（或者叫affinity matrix， 有时也叫距离矩阵）是一个有着成对相似度分数的n*n矩阵。谱聚类的这个名称是从相似度矩阵构造的矩阵的谱的使用得来。这个矩阵的特征向量被用来降维，然后再聚类。

谱聚类方法的其中一个优势是唯一的输入就是这个矩阵，并且可以被你可以想到的任何相似度度量构造出来。像K均值和层次聚类这样的方法计算特征向量的平均值，这个限制了特征（或者是描述符）对向量（为了能够计算平均值）。有了谱方法，不再需要任何类型的特征向量，只有“距离”或者“相似度”。

这里描述它是如何实现的。给定一个有着相似度分数sij的n*n的相似度矩阵S，我们可以创建一个矩阵，叫做拉普拉斯矩阵

（Laplacian matrix），

其中I是单位矩阵，D是包含S的行和的对角矩阵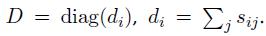，在拉普拉斯矩阵创建公式中的矩阵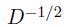表示为

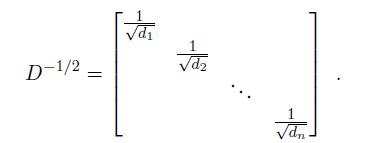
为了使得表达更加清晰，我们使用相似度元素sij的小值并且要求（术语距离矩阵也许在这个例子中更加适合）。

通过计算L的特征向量和使用对应于k个最大的特征值的k个特征向量创建一个特征向量的集合（记住我们可能会没有任何东西开始）。使用k个特征向量作为列创建一个矩阵，行将被作为新的特征向量（长度为k）。这些新的特征向量可以使用类似k均值被聚类产生最终的簇。本质上，算法做的事情是把原始的数据转换成可以被更加容易聚类的新的特征向量（在一些情况下，使用在一开始不能用的聚类算法）。

对理论足够了解之后，我们来看看应用到实际案例中的代码。同样，我们还是使用在k均值中案例中使用的字体图像。

在这个情况下，我们使用成对的欧几里德距离仅仅创建S，并计算在k个特征向量上的标准k均值聚类（在这个特殊情况下k=5）。记住矩阵V包含根据特征值排序的特征向量。最后，簇被画出来。图8表现了一个案例运行的簇（注意k均值的step在每一次运行可能会得到不同的结果）。

图8-使用拉普拉斯矩阵的特征向量生成的字体图像的谱聚类

我们也将这个案例用在我们没有任何特征向量或者任何相似度的严格定义的情况下。

对于这里提出的算法有许多不同的版本和选择。其中的每一个都有自己如何创建矩阵L和如何处理特征向量的想法。对于谱聚类和一些共同算法的更多细节可以看一看这篇论文A comparison of spectralclustering algorithms. Deepak Verma and Marina Meila. Technical report, 2003。