C语言中如何判断一个数是完全平方数

Posted 2023-05-17

怎么用C语言确定题目:一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
（要输出的是1000以内的数）
可是就是不得，我的程序如下：（跪求完整程序，谢谢了！！！）
#include<stdio.h>
#include<math.h>
int main()
int i,a,d;
double b,c,x,y;
for (i=1;i<=1000;i++)

a=i+100;
b=sqrt(a);
c=b*b;

if(c==a)

d=168+a;
x=sqrt(d);
y=x*x;
if(y==d)
printf("%d ",i);


return 0;

需要准备的材料分别有：电脑、C语言编译器。

1、首先，打开C语言编译器，新建初始.cpp文件，例如：test.cpp。

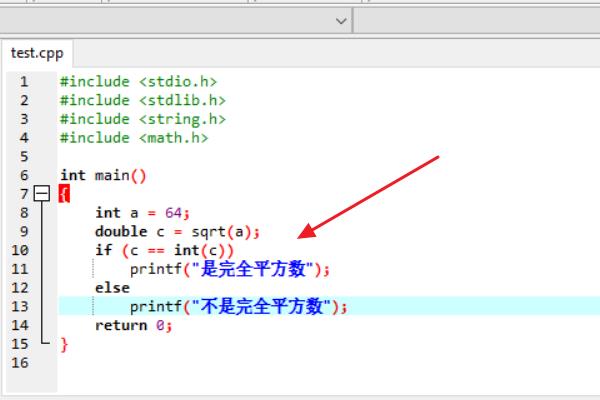
2、其次，在test.cpp文件中，输入C语言代码：

int a = 64;double c = sqrt(a);

if (c == int(c))

printf("是完全平方数");

else  

printf("不是完全平方数");

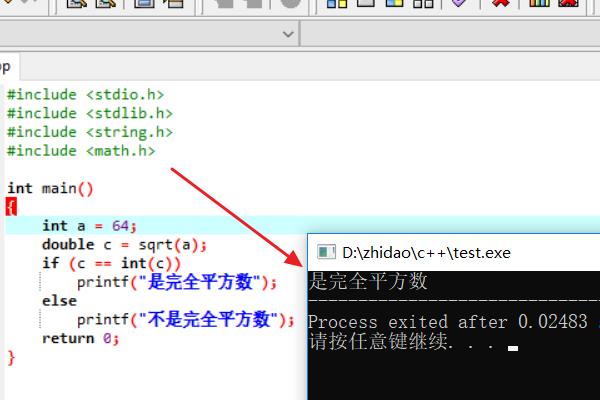
3、编译器运行test.cpp文件，此时成功快速识别出了是不是完全平方数。

参考技术A

需要准备的材料分别有：电脑、C语言编译器。

1、首先，打开C语言编译器，新建一个初始.cpp文件，例如：test.cpp。

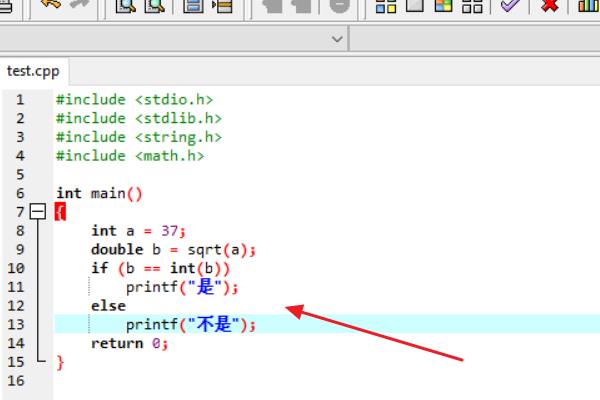
2、在test.cpp文件中，输入C语言代码：

int a = 37;double b = sqrt(a);

if (b == int(b))

printf("是");

else  

printf("不是");

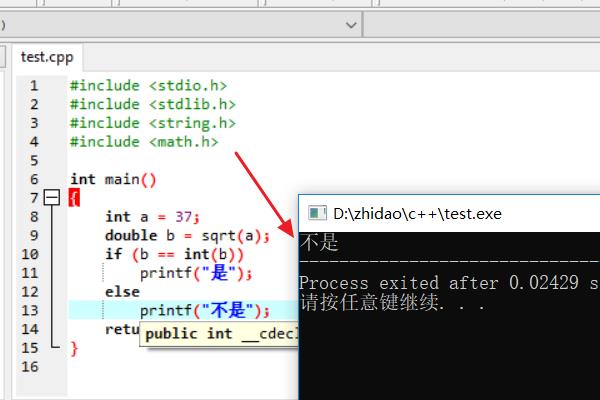
3、编译器运行test.cpp文件，此时成功输出了一个数是不完全平方数的判断结果。

参考技术B

#include&lt;stdio.h&gt;

#include&lt;math.h&gt;

int IsSquare(int n)

int i,a=0;

for(i=1;i*i&lt;=n;i++)

if(i*i==n)

a=1;

break;

return a;

int main()

int n,a;

scanf("%d",&n);

a=IsSquare(n);

if(a)

printf("YES");

else

printf("NO");

return 0;

扩展资料：

scanf函数最主要的用法是：

scanf("输入控制符",输入参数);

功能：将从键盘输入的字符转化为“输入控制符”所规定格式的数据，然后存入以输入参数的值为地址的变量中。

用scanf()函数以%s格式读入的数据不能含有空白符时，所有空白符都被当做数据结束的标志。所以题中函数输出的值只有空格前面的部分。

如果想要输出包括空格在内的所有数据，可以使用gets()函数读入数据。gets()函数的功能是读取字符串，并存放在指定的字符数组中，遇到换行符或文件结束标志时结束读入。换行符不作为读取串的内容，读取的换行符被转换为字符串结束标志'\\0'。

参考技术C

#include<stdio.h>

#include<math.h>

int main() 

long int i,x,y;

printf("完全平方数：\\n");

for(i=1;i<1000;i++)

 

x=sqrt(i+100); /*x为加上100后开方后的结果*/

y=sqrt(i+268); /*y为再加上168后开方后的结果*/

if(x*x==i+100&&y*y==i+268)/*如果一个数的平方根的平方等于该数，这说明此数是完全平方数*/

printf("\\n%ld\\n",i);

扩展资料：

C语言需要说明的是：

1、一个C语言源程序可以由一个或多个源文件组成。

2、每个源文件可由一个或多个函数组成。

3、一个源程序不论由多少个文件组成，都有一个且只能有一个main函数，即主函数。是整个程序的入口。

4、源程序中可以有预处理命令（包括include 命令，ifdef、ifndef命令、define命令），预处理命令通常应放在源文件或源程序的最前面。

5、每一个说明，每一个语句都必须以分号结尾。但预处理命令，函数头和花括号“”之后不能加分号。结构体、联合体、枚举型的声明的“”后要加“ ；”。

6、标识符，关键字之间必须至少加一个空格以示间隔。若已有明显的间隔符，也可不再加空格来间隔。

参考资料：

百度百科-c语言

参考技术D

一、数学概念：

完全平方即用一个整数乘以自己例如1*1，2*2，3*3等，依此类推。若一个数

能表示成某个整数的平方的形式，则称这个数为完全平方数。

二、算法设计：

根据概念，只要存在一个整数m，使得m*m的值为n，那么n就是完全平方数了。

于是只需要对可能的m进行遍历，即可得到n是否为完全平方数的结论了。

三、参考代码：

#include <stdio.h>
int main()

    int n,m;
    scanf("%d",&n);//输入n值。
    m = 1; //初始为最小值。
    while(m*m<n) m++;//m自加，一直到m*m>=n时退出循环。
    //此时有两种可能，一种m*m与n相等，则为完全平方数;另一种则是m*m>n, 此时不存在使得m*m=n成立的m值，n不是完全平方数。
    if(m*m==n) printf("%d 是完全平方数\\n", n);
    else printf("%d 不是完全平方数\\n", n);//输出结果。
    return 0;

[COGS 2524]__完全平方数

Description

一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数(Pefect Sqaure),也称平方数。小A认为所有的平方数都是很perfect的~

于是他给了小B一个任务:用任意个不大于n的不同的正整数相乘得到完全平方数,并且小A希望这个平方数越大越好。请你帮助小B告诉小A满足题意的最大的完全平方数。

Input

输入仅 1行,一个数n。

Output

输出仅 1 行,一个数表示答案。由于答案可以很大,

所以请输出答案对 100000007 取模后的结果。

Sample Input1

7

Sample Output1

144

Sample Input2

9

Sample Output2

5184

题解

完全平方数，要保证所有质因数的次数都是偶数，

贪心的思想，因数越多越好，我们不妨将$1～n$全选，再全部质因数分解。

若枚举到的质因数次数为奇，$-1$即可。

 1 #include <set>
 2 #include <map>
 3 #include <ctime>
 4 #include <cmath>
 5 #include <queue>
 6 #include <stack>
 7 #include <vector>
 8 #include <cstdio>
 9 #include <string>
10 #include <cstring>
11 #include <cstdlib>
12 #include <iostream>
13 #include <algorithm>
14 #define LL long long
15 #define Max(a, b) ((a) > (b) ? (a) : (b))
16 #define Min(a, b) ((a) < (b) ? (a) : (b))
17 #define sqr(x) ((x)*(x))
18 using namespace std;
19 const int N = 5000000;
20 const LL MOD = 100000007;
21 
22 int n;
23 bool isprime[N+5];
24 int q[N+5], tot;
25 int pre[N+5], cnt[N+5];
26 
27 void prepare() {
28     memset(isprime, 1, sizeof(isprime));
29     isprime[1] = false;
30     for (int i = 2; i <= n; i++) {
31     if (isprime[i]) q[++tot] = i;
32     for (int j = 1; j <= tot && i*q[j] <= n; j++) {
33         isprime[i*q[j]] = false;
34         pre[i*q[j]] = q[j];
35         if (!(i%q[j])) break;
36     }
37     }
38 }
39 
40 LL pow(LL a,LL b) {
41     LL c = 1;
42     while (b) {
43     if (b&1) c = (c*a)%MOD;
44     b >>= 1;
45     a = (a*a)%MOD;
46     }
47     return c;
48 }
49 
50 int main() {
51     scanf("%d", &n);
52     prepare();
53     for (int i = 2; i <= n; i++) {
54     int j = i;
55     while (pre[j]) {
56         cnt[pre[j]]++;
57         j /= pre[j];
58     }
59     cnt[j]++;
60     }
61     LL ans = 1;
62     for (int i = 2; i <= n; i++) ans = (ans*pow((LL)i, (LL)cnt[i]/2*2))%MOD;
63     printf("%lld\n", ans);
64     return 0;
65 }