利用Python语言计算方程的根

Posted 2023-05-16

参考技术A import math

def erfenfa(function, a, b): #定义函数，利用二分法求方程的根，function为具体方程，a,b为根的取值范围

 start = a

 end = b

 if function(a) == 0: 

  return a

 elif function(b) == 0:

  return b

 elif function(a) * function(b) > 0: 

  print("couldn't find root in [a,b]")

  return

 else:

  mid = (start + end) / 2

  while abs(start - mid) > 0.0000001: 

   if function(mid) == 0:

    return mid

   elif function(mid) * function(start) < 0:

    end = mid

   else:

    start = mid

   mid = (start + end) / 2

  return mid

def f(x):#定义构造方程式函数

 return math.pow(x, 5) -15*math.pow(x, 4) +85*math.pow(x, 3)-225*pow(x,2)+274*x - 121

print(round(erfenfa(f, 1.5, 2.4),6))

python实现迭代法求方程组的根

有方程组如下：

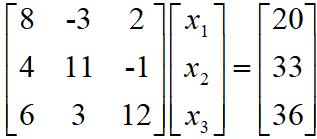
迭代法求解x，python代码如下：

import numpy as np
import matplotlib.pyplot as plt

A = np.array([[8, -3, 2], [4, 11, -1], [6, 3, 12]])
b = np.array([[20, 33, 36]])

# 方法一：消元法求解方程组的解
result = np.linalg.solve(A, b.T)
# print(\'Result:\\n\', result)

# 方法二：迭代法求解方程组的解
B = np.array([[0, 3/8, -2/8], [-4/11, 0, 1/11], [-6/12, -3/12, 0]])
f = np.array([[20/8, 33/11, 36/12]])
error = 1.0e-6
steps = 100
xk = np.zeros((3, 1))  # initialize parameter setting
errorlist = []
for k in range(steps):
    xk_1 = xk
    xk = np.matmul(B, xk) + f.T
    print(\'xk:\\n\', xk)
    errorlist.append(np.linalg.norm(xk-xk_1))
    if errorlist[-1] < error:
        print(\'iteration: \', k+1)
        break

# 把误差画出来
x_axis = [i for i in range(len(errorlist))]
plt.figure()
plt.plot(x_axis, errorlist)

结果如下：

    

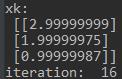
【参考文献】

《机器学习算法原理与编程实践》郑捷，第五章第一节