全球名校课程作业分享系列--斯坦福计算机视觉与深度学习CS231n之KNN

Posted 2022-12-11 寒小阳

课程作业原地址：CS231n Assignment 1
作业及整理：@郭承坤 && @Molly && @寒小阳
时间：2018年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/79138352

任务背景

用K最近邻的方法去完成图像识别的任务

代码环境

python3.6.1(anaconda4.4.0) && ubuntu16.04 测试通过

具体内容

kNN分类器是一种非常简单粗暴的分类器，它包含两个步骤：

• 训练。

读取训练数据并存储。

• 测试。

对于每一张测试图像，kNN把它与训练集中的每一张图像计算距离，找出距离最近的ｋ张图像．这ｋ张图像里，占多数的标签类别，就是测试图像的类别。

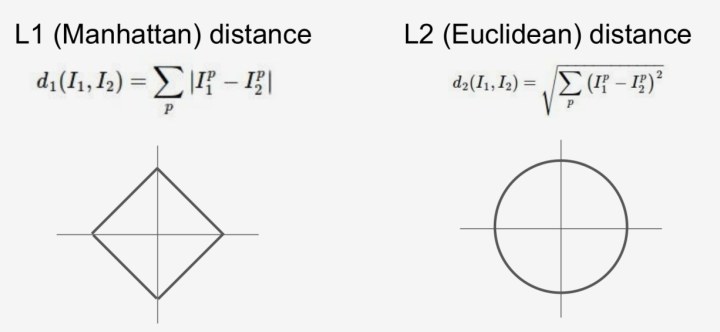
计算图像的距离有两种方式，分别是l1距离和l2距离．具体使用哪种距离度量呢？这就需要我们进一步探索啦！

• k的取值通过交叉验证得到。

对于kNN算法，k值的选择十分重要．如图所示，较小的k值容易受到噪声的干扰，较大的k值会导致边界上样本的分类有歧义．

为了得到较为合适的ｋ值，我们使用交叉验证的方法．

notebook的一些预备代码

import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt

from __future__ import print_function
from past.builtins import xrange　　　# 补充了一个库

#这里有一个小技巧可以让matplotlib画的图出现在notebook页面上，而不是新建一个画图窗口．
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # 设置默认的绘图窗口大小
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

#另一个小技巧，可以使　notebook　自动重载外部　python 模块．[点击此处查看详情][4]
#也就是说，当从外部文件引入的函数被修改之后，在notebook中调用这个函数，得到的被改过的函数．
%load_ext autoreload
%autoreload 2

加载　CIFAR-10 原始数据

# 这里加载数据的代码在 data_utils.py 中，会将data_batch_1到5的数据作为训练集，test_batch作为测试集
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

# 为了对数据有一个认识，打印出训练集和测试集的大小 
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)

输出：

Training data shape:  (50000, 32, 32, 3)
Training labels shape:  (50000,)
Test data shape:  (10000, 32, 32, 3)
Test labels shape:  (10000,)

看看数据集中的样本

这里我们将训练集中每一类的样本都随机挑出几个进行展示

classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
    idxs = np.flatnonzero(y_train == y)
    idxs = np.random.choice(idxs, samples_per_class, replace=False)
    for i, idx in enumerate(idxs):
        plt_idx = i * num_classes + y + 1
        plt.subplot(samples_per_class, num_classes, plt_idx)
        plt.imshow(X_train[idx].astype('uint8'))
        plt.axis('off')
        if i == 0:
            plt.title(cls)
plt.show()

输出

为了更高效地运行我们的代码，这里取出一个子集进行后面的练习

num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]

num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]

## 将图像数据转置成二维的

X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)

输出：

(5000, 3072) (500, 3072)

创建kNN分类器对象

记住 kNN 分类器不进行操作，只是将训练数据进行了简单的存储

from cs231n.classifiers import KNearestNeighbor
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)

现在我们可以使用kNN分类器对测试数据进行分类了。我们可以将测试过程分为以下两步：

• 首先，我们需要计算测试样本到所有训练样本的距离。
• 得到距离矩阵后，找出离测试样本最近的k个训练样本，选择出现次数最多的类别作为测试样本的类别

让我们从计算距离矩阵开始。如果训练样本有Ntr个，测试样本有Nte个，则距离矩阵应该是个　$Nte \\times Ntr$　大小的矩阵，其中元素[i,j]表示第i个测试样本到第j个训练样本的距离。

下面，打开cs231n/classifiers/k_nearest_neighbor.py，并补全 compute_distances_two_loops 方法，它使用了一个两层循环的方式（非常低效）计算测试样本与训练样本的距离．

k_nearest_neighbor.py

compute_distances_two_loops 方法

def compute_distances_two_loops(self, X):
    """
    通过一个两层的嵌套循环，遍历测试样本点，并求其到全部训练样本点的距离

    输入:
    - X: 测试数据集，一个 (num_test, D) 大小的numpy数组

    返回:
    - dists: 一个 (num_test, num_train) 大小的numpy数组，其中dists[i, j]
      表示测试样本i到训练样本j的欧式距离

    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in xrange(num_test):
      for j in xrange(num_train):
        #####################################################################
        # 任务:                                                             #
        # 计算第i个测试点到第j个训练样本点的L2距离，并保存到dists[i, j]中， #
        # 注意不要在维度上使用for循环                                       #
        #####################################################################

        dists[i, j] = np.sqrt(np.sum(np.square(self.X_train[j,:] - X[i,:])))

        #####################################################################
        #                       任务结束                                    #
        #####################################################################
    return dists

来测试一下

dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)
    `

输出：


    (500, 5000)


## 我们可以将距离矩阵进行可视化：其中每一行表示一个测试样本与所有训练样本的距离
```python
plt.imshow(dists, interpolation='none')
plt.show()




<div class="se-preview-section-delimiter"></div>

随堂测试 #1: 图中可以明显看出，有一些行或者列明显颜色较浅。（其中深色表示距离小，而浅色表示距离大）
什么原因导致图中某些行的颜色明显偏浅？
为什么某些列的颜色明显偏浅？

回答：
某些行颜色偏浅，表示测试样本与训练集中的所有样本差异较大，该测试样本可能明显过亮或过暗或者有色差。
某些列颜色偏浅，所有测试样本与该列表示的训练样本距离都较大，该训练样本可能明显过亮或过暗或者有色差。

实现 predict_labels 方法

k_nearest_neighbor.py

def predict_labels(self, dists, k=1):
    """
    通过距离矩阵，预测每一个测试样本的类别

    输入：
    - dists: 一个(num_test, num_train) 大小的numpy数组，其中dists[i, j]表示
      第i个测试样本到第j个训练样本的距离

    返回：
    - y: 一个 (num_test,)大小的numpy数组，其中y[i]表示测试样本X[i]的预测结果
    """

    num_test = dists.shape[0]
    y_pred = np.zeros(num_test)
    for i in xrange(num_test):
      # 一个长度为k的list数组，其中保存着第i个测试样本的k个最近邻的类别标签
        closest_y = []
      #########################################################################
      # 任务:                                                                 #
      # 通过距离矩阵找到第i个测试样本的k个最近邻,然后在self.y_train中找到这些 #
      # 最近邻对应的类别标签，并将这些类别标签保存到closest_y中。             #
      # 提示: 可以尝试使用numpy.argsort方法                                   #
      #########################################################################

        closest_y = self.y_train[np.argsort(dists[i])[:k]]

      #########################################################################
      # 任务:                                                                 #
      # 现在你已经找到了k个最近邻对应的标签, 下面就需要找到其中出现最多的那个   #
      # 类别标签，然后保存到y_pred[i]中。如果有票数相同的类别，则选择编号小   #
      # 的类别                                                                #
      #########################################################################

        y_pred[i] = np.argmax(np.bincount(closest_y))

      #########################################################################
      #                           END OF YOUR CODE                            # 
      #########################################################################

    return y_pred




<div class="se-preview-section-delimiter"></div>

这里我们将k设置为1 (也就是最临近算法)

y_test_pred = classifier.predict_labels(dists, k=1)




<div class="se-preview-section-delimiter"></div>

计算并打印准确率

num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))




<div class="se-preview-section-delimiter"></div>

输出：

Got 137 / 500 correct => accuracy: 0.274000

结果应该约为27%。现在，我们将k调大一点试试，令k = 5

    y_test_pred = classifier.predict_labels(dists, k=5)
    num_correct = np.sum(y_test_pred == y_test)
    accuracy = float(num_correct) / num_test
    print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))




<div class="se-preview-section-delimiter"></div>

输出：

Got 139 / 500 correct => accuracy: 0.278000

结果应该略好于k=1时的情况

现在我们将距离计算的效率提升一下，使用单层循环结构的计算方法。

实现compute_distances_one_loop方法

k_nearest_neighbor.py

def compute_distances_one_loop(self, X):
    """
    通过一个单层的嵌套循环，遍历测试样本点，并求其到全部训练样本点的距离
    输入/输出：和compute_distances_two_loops方法相同
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in xrange(num_test):

      #######################################################################
      # 任务:                                                               #
      # 计算第i个测试样本点到所有训练样本点的L2距离，并保存到dists[i, :]中  #
      #######################################################################

        dists[i,:] = np.sqrt(np.sum(np.square(self.X_train - X[i,:]),axis = 1))

      #######################################################################
      #                         任务结束                                    #
      #######################################################################
    return dists




<div class="se-preview-section-delimiter"></div>

在notebook中运行代码:

dists_one = classifier.compute_distances_one_loop(X_test)




<div class="se-preview-section-delimiter"></div>

为了保证向量化的代码运行正确，我们将运行结果与前面的方法的结果进行对比。对比两个矩阵是否相等的方法有很多，比较简单的一种是使用Frobenius范数。Frobenius范数表示的是两个矩阵所有元素的差值的均方根。或者说是将两个矩阵reshape成向量后，它们之间的欧氏距离．

difference = np.linalg.norm(dists - dists_one, ord='fro')
print('Difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')




<div class="se-preview-section-delimiter"></div>

输出：

Difference was: 0.000000
Good! The distance matrices are the same

完成完全向量化方式运行的compute_distances_no_loops方法

k_nearest_neighbor.py

def compute_distances_no_loops(self, X):
    """
    不通过循环方式，遍历测试样本点，并求其到全部训练样本点的距离
    输入/输出：和compute_distances_two_loops方法相同
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train)) 
    ######################################################################### 
    # 任务:                                                                 #
    # 计算测试样本点和训练样本点之间的L2距离，并且不使用for循环，最后将结果 #
    # 保存到dists中                                                         #
    #                                                                       #
    # 请使用基本的数组操作完成该方法；不要使用scipy中的方法           #
    #                                                                       #
    # 提示: 可以使用矩阵乘法和两次广播加法                                  #
    #########################################################################
    dists = np.multiply(np.dot(X,self.X_train.T),-2) 
    sq1 = np.sum(np.square(X),axis=1,keepdims = True) 
    #这里要将keepdims=True，使计算后依然为维度是测试样本数量的列向量
    sq2 = np.sum(np.square(self.X_train),axis=1) 
    dists = np.add(dists,sq1) 
    dists = np.add(dists,sq2) 
    dists = np.sqrt(dists)
    #########################################################################
    #                         任务结束                                      #
    #########################################################################
    return dists




<div class="se-preview-section-delimiter"></div>

在notebook中运行代码:

dists_two = classifier.compute_distances_no_loops(X_test)

将结果与之前的计算结果进行对比

difference = np.linalg.norm(dists - dists_two, ord='fro')
print('Difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')




<div class="se-preview-section-delimiter"></div>

输出：

Difference was: 0.000000
Good! The distance matrices are the same

对比一下各方法的执行速度

def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic

two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)

one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)

no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
 #理论上可以看到，完全矢量化的代码运行效率有明显的提高




<div class="se-preview-section-delimiter"></div>

输出：
具体数值可能不一样，大致意思对就可以啦

Two loop version took 78.201151 seconds
One loop version took 21.248590 seconds
No loop version took 0.137443 seconds

交叉验证

之前我们已经完成了k-Nearest分类器的编写，但是对于k值的选择很随意。下面我们将使用交叉验证的方法选择最优的超参数k。

num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []




<div class="se-preview-section-delimiter"></div>

################################################################################




<div class="se-preview-section-delimiter"></div>

# 任务:                                                                        #




<div class="se-preview-section-delimiter"></div>

# 将训练数据切分成不同的折。切分之后,训练样本和对应的样本标签被包含在数组      #




<div class="se-preview-section-delimiter"></div>

# X_train_folds和y_train_folds之中，数组长度是折数num_folds。其中              #




<div class="se-preview-section-delimiter"></div>

# y_train_folds[i]是一个矢量，表示矢量X_train_folds[i]中所有样本的标签         #




<div class="se-preview-section-delimiter"></div>

# 提示: 可以尝试使用numpy的array_split方法。                                   #




<div class="se-preview-section-delimiter"></div>

################################################################################
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)




<div class="se-preview-section-delimiter"></div>

################################################################################




<div class="se-preview-section-delimiter"></div>

#                                 结束                                         #




<div class="se-preview-section-delimiter"></div>

################################################################################




<div class="se-preview-section-delimiter"></div>

# 我们将不同k值下的准确率保存在一个字典中。交叉验证之后，k_to_accuracies[k]保　




<div class="se-preview-section-delimiter"></div>

# 存了一个长度为折数的list，值为k值下的准确率．

k_to_accuracies = 





<div class="se-preview-section-delimiter"></div>

################################################################################




<div class="se-preview-section-delimiter"></div>

# 任务:                                                                        #




<div class="se-preview-section-delimiter"></div>

# 通过k折的交叉验证找到最佳k值。对于每一个k值，执行kNN算法num_folds次，每一次  #




<div class="se-preview-section-delimiter"></div>

# 执行中，选择一折为验证集，其它折为训练集。将不同k值在不同折上的验证结果保    #




<div class="se-preview-section-delimiter"></div>

# 存在k_to_accuracies字典中。                                                  #




<div class="se-preview-section-delimiter"></div>

################################################################################
classifier = KNearestNeighbor()
for k in k_choices:
    accuracies = np.zeros(num_folds)
    for fold in xrange(num_folds):
        temp_X = X_train_folds[:]
        temp_y = y_train_folds[:]
        X_validate_fold = temp_X.pop(fold)
        y_validate_fold = temp_y.pop(fold)

        temp_X = np.array([y for x in temp_X for y in x])
        temp_y = np.array([y for x in temp_y for y in x])
        classifier.train(temp_X, temp_y)

        y_test_pred = classifier.predict(X_validate_fold, k=k)
        num_correct = np.sum(y_test_pred == y_validate_fold)
        accuracy = float(num_correct) / num_test
        accuracies[fold] =accuracy
    k_to_accuracies[k] = accuracies




<div class="se-preview-section-delimiter"></div>

################################################################################




<div class="se-preview-section-delimiter"></div>

#                                 END OF YOUR CODE                             #




<div class="se-preview-section-delimiter"></div>

################################################################################





<div class="se-preview-section-delimiter"></div>

# 输出准确率
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print('k = %d, accuracy = %f' % (k, accuracy))




<div class="se-preview-section-delimiter"></div>

输出:

k = 1, accuracy = 0.526000
k = 1, accuracy = 0.514000
k = 1, accuracy = 0.528000
k = 1, accuracy = 0.556000
k = 1, accuracy = 0.532000
k = 3, accuracy = 0.478000
k = 3, accuracy = 0.498000
k = 3, accuracy = 0.480000
k = 3, accuracy = 0.532000
k = 3, accuracy = 0.508000
k = 5, accuracy = 0.496000
k = 5, accuracy = 0.532000
k = 5, accuracy = 0.560000
k = 5, accuracy = 0.584000
k = 5, accuracy = 0.560000
k = 8, accuracy = 0.524000
k = 8, accuracy = 0.564000
k = 8, accuracy = 0.546000
k = 8, accuracy = 0.580000
k = 8, accuracy = 0.546000
k = 10, accuracy = 0.530000
k = 10, accuracy = 0.592000
k = 10, accuracy = 0.552000
k = 10, accuracy = 0.568000
k = 10, accuracy = 0.560000
k = 12, accuracy = 0.520000
k = 12, accuracy = 0.590000
k = 12, accuracy = 0.558000
k = 12, accuracy = 0.566000
k = 12, accuracy = 0.560000
k = 15, accuracy = 0.504000
k = 15, accuracy = 0.578000
k = 15, accuracy = 0.556000
k = 15, accuracy = 0.564000
k = 15, accuracy = 0.548000
k = 20, accuracy = 0.540000
k = 20, accuracy = 0.558000
k = 20, accuracy = 0.558000
k = 20, accuracy = 0.564000
k = 20, accuracy = 0.570000
k = 50, accuracy = 0.542000
k = 50, accuracy = 0.576000
k = 50, accuracy = 0.556000
k = 50, accuracy = 0.538000
k = 50, accuracy = 0.532000
k = 100, accuracy = 0.512000
k = 100, accuracy = 0.540000
k = 100, accuracy = 0.526000
k = 100, accuracy = 0.512000
k = 100, accuracy = 0.526000




<div class="se-preview-section-delimiter"></div>

plot the raw observations

画个图会更直观一点

for k in k_choices:
    accuracies = k_to_accuracies[k]
    plt.scatter([k] * len(accuracies), accuracies)

    # plot the trend line with error bars that correspond to standard deviation
    # 画出在不同k值下，误差均值和标准差
    accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
    accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
    plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
    plt.title('Cross-validation on k')
    plt.xlabel('k')
    plt.ylabel('Cross-validation accuracy')
    plt.show()




<div class="se-preview-section-delimiter"></div>

根据上面交叉验证的结果，选择最优的k，然后在全量数据上进行试验，你将得到超过28%的准确率。

best_k = 10

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)





<div class="se-preview-section-delimiter"></div>

# 计算并显示准确率
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

输出：

Got 141 / 500 correct => accuracy: 0.282000

本次作业小结：

本文代码在python3.6.1中测试通过.本节用到的最近邻算法在实践中很少用于图片分类任务中。这次作业的主要任务，是让大家了解最近邻算法的思想，同时掌握使用矢量运算代替for循环的方法，还有就是掌握交叉验证的方法。课上说随机选择的交叉验证参数一般优于网格式选择的参数，但是作业当中依然使用了网格式选择的k值，同学们可以将这部分代码进行优化，实现随机选择k值进行交叉验证。