二进制二项式定理组合数C. Moamen and XOR

Posted 行码棋

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二进制二项式定理组合数C. Moamen and XOR相关的知识，希望对你有一定的参考价值。

相同知识点的题目

https://blog.csdn.net/qq_50285142/article/details/122792736

前置知识

  • 二项式系数之和： C n 0 + C n 1 + C n 2 + C n 3 + . . . + C n n − 1 + C n n = 2 n C_n^0+C_n^1+C_n^2+C_n^3+...+C_n^n-1+C_n^n=2^n Cn0​+Cn1​+Cn2​+Cn3​+...+Cnn−1​+Cnn​=2n
  • 二项式奇数项系数之和等于偶数项系数之和，即
    C n 1 + C n 3 + C n 5 + . . . = C n 0 + C n 2 + C n 4 + C n 6 + . . . = 2 n − 1 C_n^1+C_n^3+C_n^5+...=C_n^0+C_n^2+C_n^4+C_n^6+...=2^n-1 Cn1​+Cn3​+Cn5​+...=Cn0​+Cn2​+Cn4​+Cn6​+...=2n−1

题目链接

https://codeforces.com/problemset/problem/1557/C


长度为n的数组每个元素不超过 2 k 2^k 2k，问满足 a 1   &   a 2   &   a 3   &   …   &   a n ≥ a 1 ⊕ a 2 ⊕ a 3 ⊕ … ⊕ a n a_1 \\,\\&\\, a_2 \\,\\&\\, a_3 \\,\\&\\, \\ldots \\,\\&\\, a_n \\ge a_1 \\oplus a_2 \\oplus a_3 \\oplus \\ldots \\oplus a_n a1​&a2​&a3​&…&an​≥a1​⊕a2​⊕a3​⊕…⊕an​的数组个数

对每一位二进制进行考虑，可以认为数组中的每个数共有k位二进制位

对数组中的数考虑形式如下图：（我认为应该在脑中形成模型）

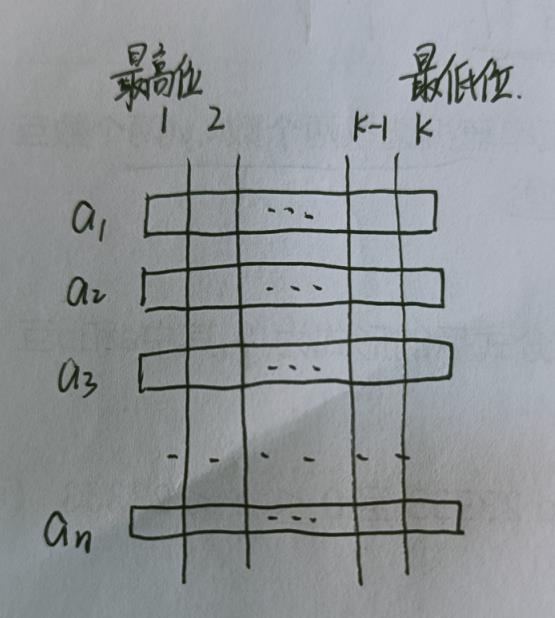
我们考虑每一位的情况：

我们需要分奇偶进行考虑：考虑当前位相等和大于的情况（题目中是大于等于，分开考虑）

  • n为奇数
    • 相等: 共 d 1 = C n 0 + C n 2 + C n 4 + . . . + C n n − 1 + C n n = 2 n − 1 + 1 d_1=C_n^0+C_n^2+C_n^4+...+C_n^n-1+C_n^n=2^n-1+1 d1​=Cn0​+Cn2​+Cn4​+...+Cnn−1​+Cnn​=2n−1+1
      • 数组中的数该位全为1 : C n n C_n^n Cnn​
      • 数组中的数该位全为0: C n 0 C_n^0 Cn0​
      • 该位有偶数个1,且存在0: C n 2 + C n 4 + . . . + C n n − 1 C_n^2+C_n^4+...+C_n^n-1 Cn2​+Cn4​+...+Cnn−1​ (注意n为奇数)
    • 大于： 不存在
  • n为偶数
    • 相等: 共 d 2 = C n 0 + C n 2 + C n 4 + . . . + C n n − 2 = 2 n − 1 − 1 d_2=C_n^0+C_n^2+C_n^4+...+C_n^n-2=2^n-1-1 d2​=Cn0​+Cn2​+Cn4​+...+Cnn−2​=2n−1−1
      • 该位有偶数个1,且存在0: C n 2 + C n 4 + . . . + C n n − 2 C_n^2+C_n^4+...+C_n^n-2 Cn2​+Cn4​+...+Cnn−2​
      • 数组中的数该位全为0: C n 0 C_n^0 Cn0​
    • 大于:
      • 数组中的数该位全为1: C n n = 1 C_n^n=1 Cnn​=1

接下来算结果：