图解贝叶斯公式

Posted 2022-12-09 ESOO

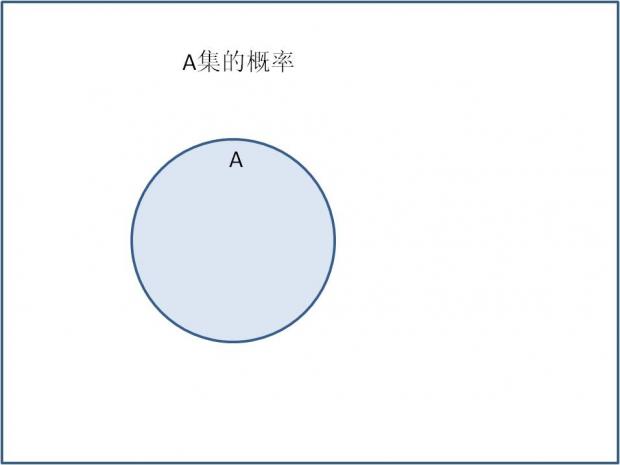
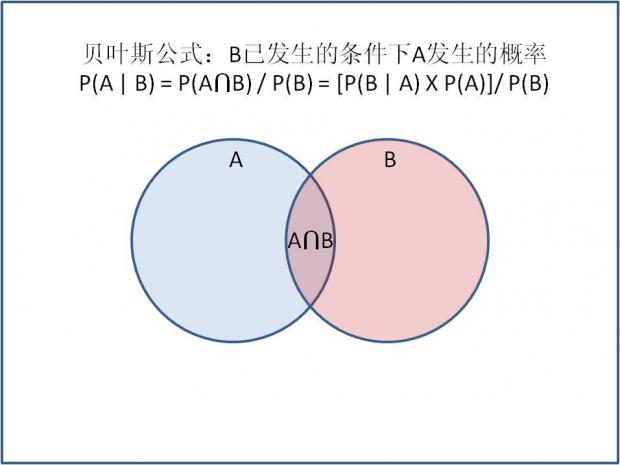
概率，顾名思义其实就是一个比率。A发生的概率相当于A集的面积与全集总面积的比率。

贝叶斯概率

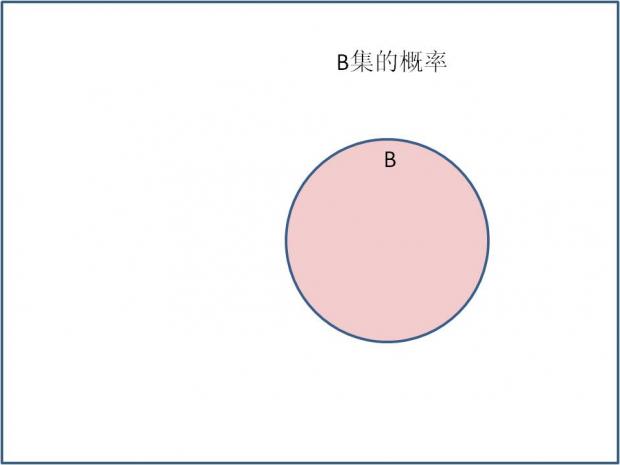
B发生的概率相当于B集的面积与全集总面积的比率。

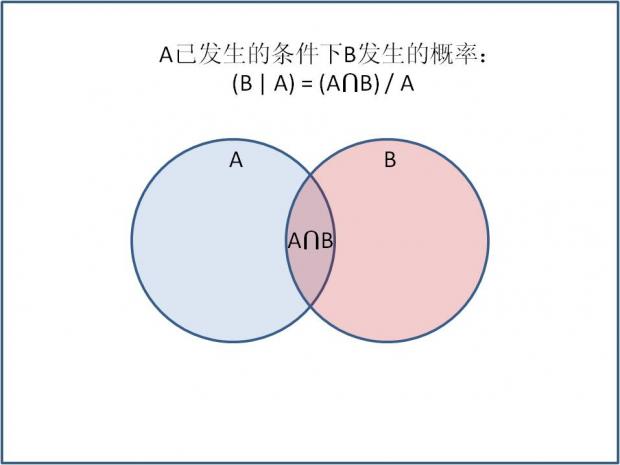
AB都发生的概率相当于AB交集的面积与全集总面积的比率。

B已经发生条件下A发生的概率相当于AB交集的面积与B面积的比率。由于B已经发生，在这里是全集，所以要比上B的面积。

A已经发生条件下B发生的概率相当于AB交集的面积与A面积的比率。由于A已经发生，在这里是全集，所以要比上A的面积。

简单的公式推导得出AB交集的概率。

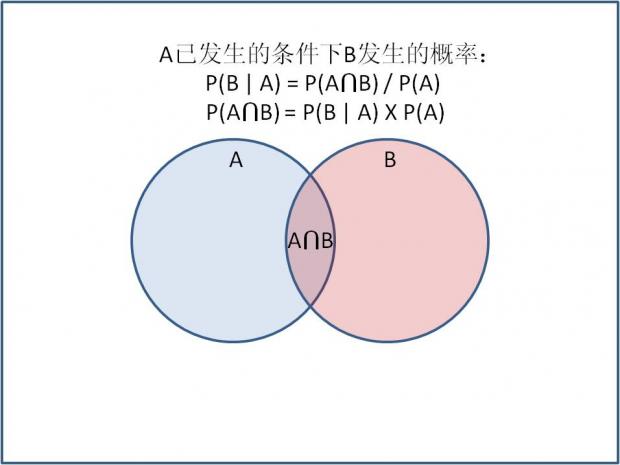
代入前面公式，得出著名的贝叶斯公式。

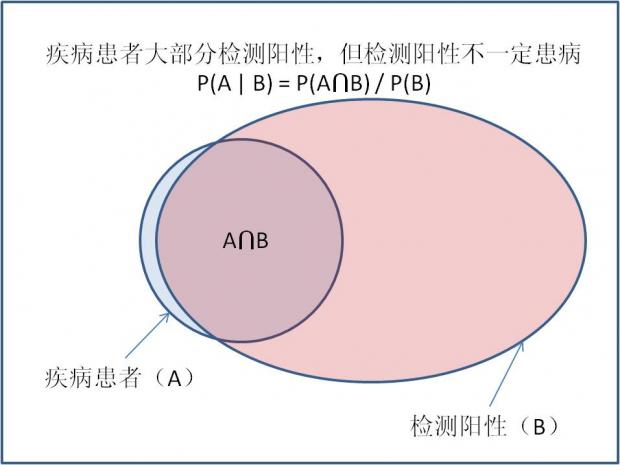
用贝叶斯公式直观解释为什么即使某疾病患者绝大部分检测为阳性，但一个人检测为阳性时，患该病的概率不一定很高。

 

全概率公式：(http://zh.wikipedia.org/zh-cn)

 

假设 Bn : n = 1, 2, 3, ... 是一个概率空间的有限或者可数无限的分割（既 Bn为一完备事件组），且每个集合Bn是一个可测集合，则对任意事件A有全概率公式：

Pr ( A ) = ∑ n Pr ( A ∩ B n ) \\displaystyle \\Pr(A)=\\sum _n\\Pr(A\\cap B_n)\\, 点击打开链接

又因为

Pr ( A ∩ B n ) = Pr ( A ∣ B n ) Pr ( B n ) , \\displaystyle \\Pr(A\\cap B_n)=\\Pr(A\\mid B_n)\\Pr(B_n),

此处Pr(A | B)是B发生后A的条件概率，所以全概率公式又可写作：

Pr ( A ) = ∑ n Pr ( A ∣ B n ) Pr ( B n ) . \\displaystyle \\Pr(A)=\\sum _n\\Pr(A\\mid B_n)\\Pr(B_n).\\,

全概率公式将对一复杂事件A的概率求解问题转化为了在不同情况或不同原因 Bn下发生的简单事件的概率的求和问题