机器学习入门系列03,Error的来源:偏差和方差(bias 和 variance)
Posted yofer张耀琦
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习入门系列03,Error的来源:偏差和方差(bias 和 variance)相关的知识,希望对你有一定的参考价值。
Gitbook整理地址:https://yoferzhang.gitbooks.io/machinelearningstudy/content/20170327ML03BiasAndVariance.html
回顾
第二篇中神奇宝贝的例子:
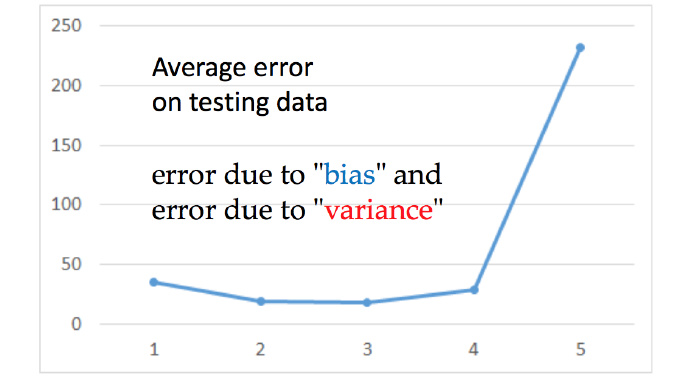
可以看出越复杂的model 再测试集上的性能并不是越好
这篇要讨论的就是 error 来自什么地方?
error主要的来源有两个,bias(偏差) 和 variance(方差)
估测

假设上图为神奇宝贝cp值的真正方程,当然这只有Niantic(制作《Pokemon Go》的游戏公司)知道。从训练集中可以找到真实方程 f̂ 的近似方程 f∗ 。
估测bias 和 variance
估测变量 x 的平均值
- 假设
x 的平均值为 μ ,方差为 σ2估测平均值怎么做呢?
- 首先拿到N个样品点: x1,x2,…,xN
- 计算平均值得到
m
,
m=1N∑nxn≠μ

但是如果计算很多组的m ,然后求m的期望
E[m]=E[1N∑nxn]=1N∑nE[xn]=μ
这个估计呢是无偏估计(unbiased)。
然后m分布对于 μ 的离散程度(方差):
Var[m]=σ2N
这主要取决于N,下图可看出N越小越离散

估测变量 x 的方差
首先用刚才的方法估测m,
m=1N∑nxn≠μ 然后再做下面计算:
s2=1N∑n(xn−m)2
就可以用 s2 来估测 σ2

这个估计是有偏估计(biased),
求 s2 的期望值:
E[s2]=N−1Nσ2≠σ2
用靶心来说明一下bias和variance的影响

靶心为真正的方程 f̂ ,深蓝色点为 f∗ ,是实验求得的方程。求 f∗ 的期望值 f¯=E[f∗] ,即图中浅蓝色的点。
f¯ 和 f̂ 之间的距离就是误差 bias,而