[数据结构]tree-form data structure summary
Posted yccy1230
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[数据结构]tree-form data structure summary相关的知识,希望对你有一定的参考价值。
树形数据结构小结
一、 说明
小结中包括Binary Tree、Binary search tree、buildable tree、AVL tree、Splay tree、Tries、B-trees。主要对这些学过的树形数据结构做一个简单的总结概括,可能不是很全面,但可作为复习参考。
二、 正文
1) Binary_trees:
① 定义:空树或者父节点具有之多两个孩子节点的树
② 概念:
· 完全二叉树:除最后一层外,其它层中节点树均达到最大,最后一层叶子节点由左向右排列。
· 满二叉树:每一层节点数均达到最大值
· 深度(depth):二叉树的层数(一般越矮越好)
③ 性质:以下记二叉树的根节点所在层数为第一层
· 第i层的节点不超过2^(i-1)个
· 深度为h的二叉树至多有2^h-1个节点(h>=1)
· 具有n个节点的完全二叉树depth=log2n+1
④ 二叉树的三种遍历形式:
· VLR 前序遍历(preorder):根->左->右
· LVR 中序遍历(inorder):左->根->右
· LRV后序遍历(postorder):左->右->根
⑤ 重要算法描述:
· 层序遍历:要求对树进行逐层遍历
算法描述:利用辅助队列存储待访问的节点指针
1)、将根节点放入队列
2)、对队列的队首进行访问,同时对当前访问节点的左右孩子进行检测,若非空,对其进行入队操作
3)、将已访问的队首pop出来
4)、重复上述操作,直至辅助队列中为空
实现代码:
template<class Entry>
void Binary_tree<Entry>::level_tranverse(void(*visit)(Entry &))
if (!root)return;
queue<Binary_node<Entry> *> wait_queue;
wait_queue.push(root);
do
Binary_node<Entry> *tmp = wait_queue.front();
(*visit)(tmp->data);
if (tmp->left_child)wait_queue.push(tmp->left_child);
if (tmp->right_child)wait_queue.push(tmp->right_child);
wait_queue.pop();
while (!wait_queue.empty());
- 左右交换(interchange):将每个节点的左右子树进行交换
算法描述:利用递归实现
1)base case:当传入根节点为空时,结束递归
2)general case:sub_root->left=sub_root->right
Sub_root->right=sub_root->left
对左右子树分别进行上述递归
实现代码:
template<class Entry>
void Binary_tree<Entry>::interchange()
recursive_interchange(root);
template<class Entry>
void Binary_tree<Entry>::recursive_interchange(Binary_node<Entry>* sub_root)
if (!sub_root)
Binary_node<Entry> *tmp = sub_root->left_child;
sub_root->left_child = sub_root->right_child;
sub_root->right_child = tmp;
recursive_interchange(sub_root->left_child);
recursive_interchange(sub_root->right_child);
· 深度检测(depth计算):对任意树的depth进行计算
算法描述:利用递归实现
1)、base case:当传入根节点为空时,返回depth=0,结束递归
2)、general case:拿到左右子树的depth(通过递归,记为 left、right)
若右子树深度大于左子树,则返回(right+1);
若左子树深度大于右子树,则返回(left+1);
其中+1表示根节点的深度1.
实现代码:
template<class Entry>
int Binary_tree<Entry>::height()
return recursive_height(root);
template<class Entry>
int Binary_tree<Entry>::recursive_height(Binary_node<Entry>* sub_root)
if (!sub_root)return 0;
int left = recursive_height(sub_root->left_child);
int right = recursive_height(sub_root->right_child);
if (left > right) return (left + 1);
else return (right + 1);
· 节点数计算(size计算):
算法描述:利用递归实现
1)、base case:当传入根节点为空时,返回size=0,结束递归
2)、general case:取得左右子树的size(通过递归,记为left、right),返回(left+right+1)。
其中+1表示当前根节点。
实现代码:
template<class Entry>
int Binary_tree<Entry>::size()
return recursive_size(root);
template<class Entry>
int Binary_tree<Entry>::recursive_size(Binary_node<Entry>* sub_root)
if (!sub_root)return 0;
int left = recursive_size(sub_root->left_child);
int right = recursive_size(sub_root->right_child);
return (left + right + 1);
· 前序遍历(preorder):
算法描述:利用递归实现
1)base case:当传入根节点为空时,结束递归
2)general case:对根节点进行访问;
然后对左孩子进行访问(递归进行);
最后对右孩子进行访问(递归进行);
实现代码:
template<class Entry>
void Binary_tree<Entry>::preorder(void(*visit)(Entry &))
recursive_preorder(root, visit);
template<class Entry>
void Binary_tree<Entry>::recursive_preorder(Binary_node<Entry>* sub_root, void(*visit)(Entry &))
if (sub_root)
(*visit)(sub_root->data);
recursive_preorder(sub_root->left_child, visit);
recursive_preorder(sub_root->right_child, visit);
· 中序遍历和后序遍历与前序遍历类似就不再赘述。
-----------------------------------------华丽丽的分割线-------------------------------------------
2) Binary_Search_Tree:
①定义:空树或是一棵具有如下性质的树:
1) 左子树上的节点值均小于根节点的值
2) 右子树上的节点值均大于根节点的值
3) 树上不存在节点值相同的两个节点
4) 左右子树也是一棵二叉查找树
②重要算法描述:
· 查找算法(search)
算法描述:利用递归实现
1)、base case:若当前根节点值等于待查找的值返回sub_root指针,或当前根节点为空,返回NULL
2)、general case:若当前根节点值大于待查找节点值,则对当前节点的左子树进行查找(递归进行)
若当前节点值小于待查找节点值,则对当前节点的右子树进行查找(递归进行)
实现代码:
template<class Record>
Error_code Binary_search_tree<Record>::search(Record & item)
Binary_node<Record> *p = recursive_search(root, item);
if (p == NULL)return not_present;
else
item = p->data;
return success;
template<class Record>
Binary_node<Record> * Binary_search_tree<Record>::recursive_search(Binary_node<Record>*& sub_root, const Record & item)
if (sub_root == NULL || sub_root->data == item)return sub_root;
else if (sub_root->data > item)return recursive_search(sub_root->left_child, item);
else if (sub_root->data < item)return recursive_search(sub_root->right_child, item);
· 插入算法(insert)
算法描述:利用递归实现,下附循环实现代码
1)base case:若当前根节点为空,则sub_root=new node;
或当前根节点的值与待插入节点值相等,返回duplicate error
2)general case:若当前根节点值大于待插入节点值,则转化为
对当前节点的左子树进行插入(递归进行)
若当前根节点值小于待插入节点值,则转化为对当前节点的右子树进行插入(递归进行)
实现代码:
//递归版本
template<class Record>
Error_code Binary_search_tree<Record>::insert(const Record & item)
if (recursive_insert(root, item) == success)
count++;
return success;
else return duplicate_error;
template<class Record>
Error_code Binary_search_tree<Record>::recursive_insert(Binary_node<Record>*& sub_root, const Record & item)
if (!sub_root)
sub_root = new Binary_node<Record>(item);
return success;
else if (sub_root->data > item)return recursive_insert(sub_root->left_child, item);
else if (sub_root->data < item)return recursive_insert(sub_root->right_child, item);
else return duplicate_error;
//循环版本
template<class Record>
Error_code Binary_search_tree<Record>::c_insert(const Record & item)
Binary_node<Record> *current=root, *previous=root;
if(!current)root = new Binary_node<Record>(item);
else
while (current != NULL)
previous = current;
if (current->data > item)current = current->left_child;
else if (current->data < item)current = current->right_child;
else return duplicate_error;
if (previous->data > item)
previous->left_child = new Binary_node<Record>(item);
else
previous->right_child = new Binary_node<Record>(item);
return success;
· 删除算法(remove)
算法描述:利用递归实现,下附循环实现代码
1)、base case:若传入根节点为空,则返回not presen
若当前根节点的值等于待删除节点的值,则对当前根节点进行删除操作(删除操作在下面进行详述)
2)、general case:若当前根节点的值大于待删除节点的值,则转化为对当前节点的左子树进行删除操作(递归进行)
若当前根节点的值小于待删除节点的值,则转化为对当前节点的右子树进行删除操作(递归进行)
删除操作(destroy):
/*precondition:传入指针指向待删除节点*/
1)若传入待删除节点为空,则返回not present
2)若传入待删除节点的左子树为空,则将传入指针修改为sub_root->right
3) 若传入待删除节点的右子树为空,则将传入指针修改为sub_root->left
4)若传入待删除节点的左右指针均不为空,则寻找待删除节点的前驱(左子树中最大值),将待删除节点值修改为前驱值,转化为删除前驱节点(右子树必为空)
ATTENTION:要注意若待删除节点的左子树有且仅有一个节点的情况。
代码实现:
//递归版本
template<class Record>
Error_code Binary_search_tree<Record>::remove(const Record & item)
if (search_and_destroy(root, item) == success)
count--;
return success;
else return not_present;
template<class Record>
Error_code Binary_search_tree<Record>::search_and_destroy(Binary_node<Record>*& sub_root, const Record & item)
if (sub_root == NULL || sub_root->data == item)
return destroy(sub_root);
else if (sub_root->data > item)return destory(sub_root->left_child);
else if (sub_root->data < item)return destory(sub_root->right_child);
template<class Record>
Error_code Binary_search_tree<Record>::destroy(Binary_node<Record>*& sub_root)
if (sub_root == NULL)return not_present;
Binary_node<Entry> *to_delete = sub_root;
if (sub_root->left_child == NULL) sub_root = sub_root->right_child;
else if (sub_root->right_child == NULL) sub_root = sub_root->left_child;
else
to_delete = sub_root->left_child;
Binary_node<Entry> *parent = sub_root;
while (!to_delete->right_child)
parent = to_delete;
to_delete = to_delete->right_child;
sub_root->data = to_delete->data;
if (parent == sub_root)sub_root->left_child = to_delete->left_child; //Special condition:no right_child under to_delete
else parent->right_child = to_delete->right_child;
delete to_delete;
return success;
//循环版本
template<class Record>
Error_code Binary_search_tree<Record>::c_remove(const Record & item)
if (root == NULL || root->data == item)
return destroy(root);
else
Binary_node<Record> *&tmp = root;
while (tmp != NULL)
if (tmp->data > item)tmp = tmp->left_child;
else if (tmp->data < item)tmp = tmp->right_child;
else return destroy(tmp);
return not_present;
-----------------------------------------华丽丽的分割线-------------------------------------------
以下描述的各个树实际上是在对Binary Search Tree的insert进行各种环境下的优化操作。
3)Bulidable tree:/*precondition:待插入节点为顺序时方可使用该算法*/
算法描述:
1)、 判断该节点位于的层数。X%2k=0 ,K为满足条件的最大值。在10.3节,层数从叶子节点开始计算。叶子节点位第0层。
2)、 节点的右孩子默认为空(该节点为树中的最大值)。节点如果为叶子节点,左孩子为空。节点如果为非叶子节点,找到k-1层的最后一个节点为左孩子。
3)、 关于增加节点的父节点判断,如果K+1层存在,K+1层的最后一个节点的右孩子为空,当前点为K+1最后一个节点的右孩子。
在最后一个节点插入成功之后,需要进行右孩子的处理:
4)、从最高层n依次向叶子节点方向查找,如果当前第k层的最后一个节点node的右孩子为空。
依次查找第K-1层到1层的最后一个节点,如果当前层i的最后一个节点比K层的最后一个节点node大,则找到它的右孩子。
继续从第i层向第3层搜索,处理右孩子的链接。直到搜索到第3层为止。(叶子节点为第1层)
ATTENTION:完成插入操作的关键,记住每一层最后一个节点的位置(指针)。
因此,为了完成插入操作,引入一个辅助队列:
List<Binary_node<entry>* > last_node;
last_node为List的对象,其中的每一个元素用来记录插入过程中每一个层最后一个节点的指针。 last_node的第0个元素初始化为空,叶子节点层记录在last_node的第1个元素中,依次类推。
构建方法简述:
1)从有序序列中依次取出每个节点,按照Buildable Tree的构建方法在树中插入该节点。
2)全部节点插入成功之后,分析每层最后一个节点的右孩子是否链接成功,依次处理每一层右孩子的连接。
3)右孩子的链接处理之后,获取当前二叉查找树的根,构建结束。
当前二叉查找树根的地址存放于last_node的最后一个元素中。
实现代码:
template <class Record>
Error_code Buildable_tree<Record> ::build_tree(const List<Record> &supply)
Error_code ordered_data = success;
//remove it for our Binary_tree int count
//int count = 0; // number of entries inserted so far
Record x, last_x;
List < Binary_node<Record> * > last_node;
// pointers to last nodes on each level
Binary_node<Record> *none = NULL;
last_node.insert(0, none); // permanently NULL (for children of leaves)
while (supply.retrieve(count, x) == success)
if (count > 0 && x <= last_x)
ordered_data = fail;
break;
build_insert(++count, x, last_node);
last_x = x;
root = find_root(last_node);
connect_trees(last_node);
return ordered_data; // Report any data-ordering problems back to client.
template <class Record>
Error_code Buildable_tree<Record> ::build_tree(const List<Record> &supply)
Error_code ordered_data = success;
//remove it for our Binary_tree int count
//int count = 0; // number of entries inserted so far
Record x, last_x;
List < Binary_node<Record> * > last_node;
// pointers to last nodes on each level
Binary_node<Record> *none = NULL;
last_node.insert(0, none); // permanently NULL (for children of leaves)
while (supply.retrieve(count, x) == success)
if (count > 0 && x <= last_x)
ordered_data = fail;
break;
build_insert(++count, x, last_node);
last_x = x;
root = find_root(last_node);
connect_trees(last_node);
return ordered_data; // Report any data-ordering problems back to client.
template <class Record>
Binary_node<Record> *Buildable_tree<Record> ::find_root(
const List < Binary_node<Record>* > &last_node)
/* Pre: The list last node contains pointers to the last node on each occupied level of the binary search tree.
Post: A pointer to the root of the newly created binary search tree is returned.
Uses: Methods of classList */
Binary_node<Record> *high_node;
last_node.retrieve(last_node.size() - 1, high_node);
// Find root in the highest occupied level in last node .
return high_node;
template <class Record>
void Buildable_tree<Record> :: (
const List < Binary_node<Record>* > &last_node)
Binary_node<Record>
*high_node, // from last node with NULL right child
*low_node; // candidate for right child of high node
int high_level = last_node.size() - 1, low_level;
while (high_level > 2) // Nodes on levels 1 and 2 are already OK.
last_node.retrieve(high_level, high_node);
if (high_node->right != NULL)
high_level--; // Search down for highest dangling node.
else // Case: undefined right tree
low_level = high_level;
do // Find the highest entry not in the left subtree.
last_node.retrieve(--low_level, low_node);
while (low_node != NULL && low_node->data < high_node->data);
high_node->right = low_node;
high_level = low_level;
4)AVL Tree:
①定义:在AVL树中任何节点的两个子树的高度最大差别为一的一棵二分查找树
②实现原理:在原有的节点中加入平衡因子(balance factor):左高(left_higher),右高(right_higher),等高(equal_height).若出现破坏平衡的情况,则立即进行对应情况的旋转进行调整,以维持平衡(减小高度)。使得最终的AVL树各个节点的左右子树高度差不超过1.
③四种操作使用情况及其效果(感谢@collonn提供的AVL图解CSDN):
· LL
当前节点为左高,且当前节点的左孩子也为左高
操作:对当前节点进行一次右旋
效果:高度--,当前节点与左孩子平衡因子调整为等高
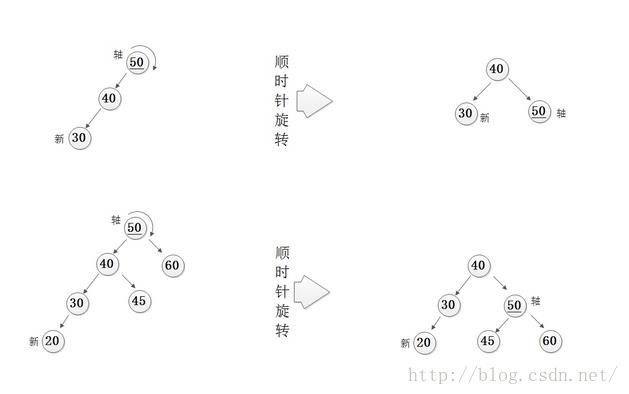
· RR
当前节点为右高,且当前节点的右孩子也为右高
操作:对当前节点进行一次左旋
效果:高度--,当前节点与右孩子的平衡因子调整为等高
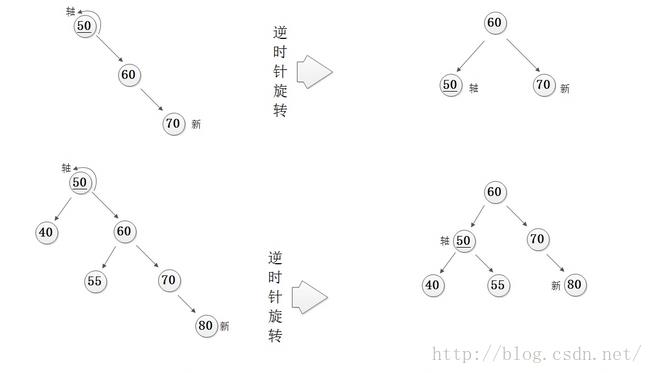
· LR
当前结点为左高,且左孩子为右高
操作:先对左孩子进行一次左旋,再对当前节点进行一次右旋
效果: 高度--,当前节点的平衡因子调整为等高,左孩子的平衡因子由左孩子的右孩子确定
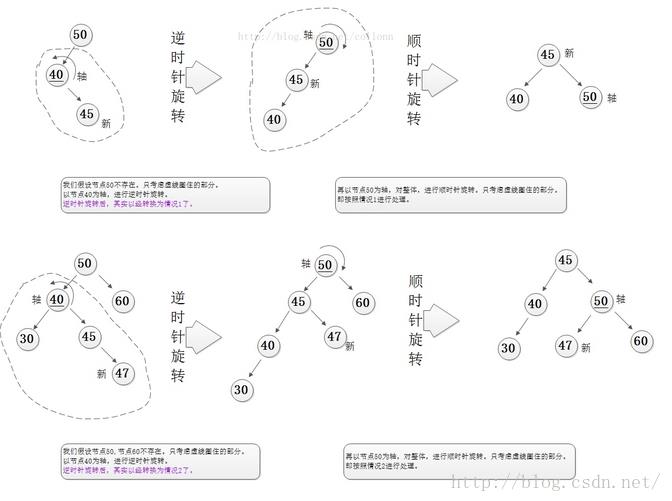
· RL
当前节点为右高,且当前节点的有孩子为左高
操作:先对右孩子进行一次右旋,在对当前节点进行一次左旋
效果:高度--,当前节点的平衡因子调整为等高,右孩子的平衡因子由右孩子的左孩子确定
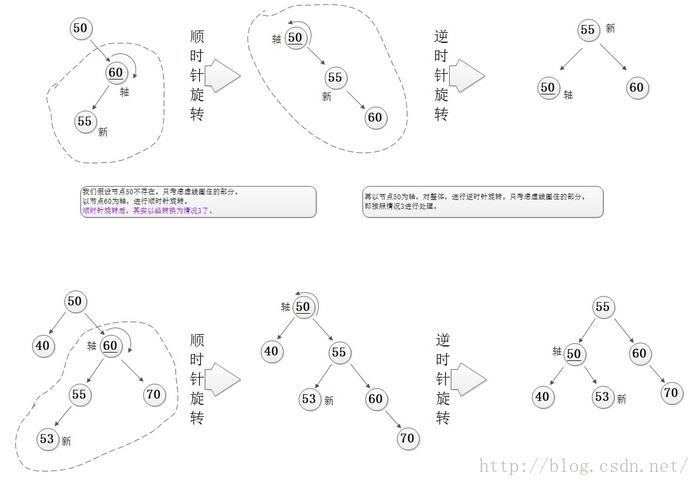
④操作:
1)单一旋转:
· 左旋:

实现代码:
template<class Record>
void AVL_tree<Record>::rotate_left(Binary_node<Record>*& sub_root)
if (sub_root == nullptr || sub_root->right_child == nullptr)
cout << "WARNING:program error detected in rotate left" << endl;
else
Binary_node<Record> *right_tree = sub_root->right_child;
sub_root->right_child = right_tree->left_child;
right_tree->left_child = sub_root;
sub_root = right_tree;
· 右旋:
实现代码:
template<class Record>
void AVL_tree<Record>::rotate_right(Binary_node<Record>*& sub_root)
if (sub_root == nullptr || sub_root->left_child == nullptr)
cout << "WARNING:program error detected in rotate right" << endl;
else
Binary_node<Record> *left_tree = sub_root->left_child;
sub_root->left_child = left_tree->right_child;
left_tree->right_child = sub_root;
sub_root = left_tree;
2)组合旋转:
· LR/LL

实现代码:
template<class Record>//先调整平衡因子,然后进行对应的旋转
void AVL_tree<Record>::left_balance(Binary_node<Record>*& sub_root)
Binary_node<Record> *&left_tree = sub_root->left_child;
switch (left_tree->get_balance())
case left_higher: //LL
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
rotate_right(sub_root);
break;
case equal_height:
cout << "WARNING:program error detected in left balance" << endl;
break;
case right_higher: //LR: Pay attention to the balance_facor
Binary_node<Record> *sub_tree = left_tree->right_child;
switch (sub_tree->get_balance())
case equal_height:
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(equal_height);
left_tree->set_balance(left_higher);
break;
case left_higher:
sub_root->set_balance(right_higher);
left_tree->set_balance(equal_height);
break;
sub_tree->set_balance(equal_height);
rotate_left(left_tree);
rotate_right(sub_root);
break;
· RL/RR
template<class Record>
void AVL_tree<Record>::right_balance(Binary_node<Record>*& sub_root)
Binary_node<Record> *&right_tree = sub_root->right_child;
switch (right_tree->get_balance())
case right_higher: //RR:对sub_root左旋
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
rotate_left(sub_root);
break;
case equal_height:
cout << "WARNING:program error detected in right balance" << endl;
break;
case left_higher: //RL:右旋后左旋,注意平衡因子的判断
Binary_node<Record> *sub_tree = right_tree->left_child;
switch (sub_tree->get_balance())
case equal_height:
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(equal_height);
right_tree->set_balance(right_higher);
break;
case right_higher:
sub_root->set_balance(left_higher);
right_tree->set_balance(equal_height);
break;
sub_tree->set_balance(equal_height);
rotate_right(right_tree);
rotate_left(sub_root);
break;
⑤重要算法描述;
· 插入操作:
算法描述:递归实现
1)base case:当前节点为空时,sub_root=new node,返回success
或当前节点值的待插入节点值返回duplicate error
2)general case:若当前节点值大于待插入节点值,则转化为对当前节点的左子树进行插入操作(递归进行),若左子树taller=true,判断是否破坏了平衡,如果破坏了平衡,寻找对应操作,并调整平衡因子;
若当前节点值小于待插入节点值,则转化为对当前节点的右子树进行插入操作(递归进行),同样进行上述判断、操作。
实现代码;
template<class Record>
Error_code AVL_tree<Record>::insert(const Record & new_data)
bool taller;
return avl_insert(root, new_data, taller);
template<class Record>
Error_code AVL_tree<Record>::avl_insert(Binary_node<Record>*& sub_root, const Record & new_data, bool & taller)
if (sub_root == NULL)
sub_root = new AVL_node<Record>(new_data);
taller = true;
return success;
else if (sub_root->data == new_data)
taller = false;
return duplicate_error;
else if (sub_root->data > new_data)
Error_code result = avl_insert(sub_root->left_child, new_data, taller);
if (taller == true)
switch (sub_root->get_balance())
case left_higher:
left_balance(sub_root);
taller = false;
break;
case equal_height:
sub_root->set_balance(left_higher);
break;
case right_higher:
sub_root->set_balance(equal_height);
taller = false;
break;
return result;
else
Error_code result = avl_insert(sub_root->right_child, new_data, taller);
if (taller == true)
switch (sub_root->get_balance())
case left_higher:
sub_root->set_balance(equal_height);
taller = false;
break;
case equal_height:
sub_root->set_balance(right_higher);
break;
case right_higher:
right_balance(sub_root);
taller = false;
break;
return result;
· 删除操作:
算法描述:递归实现
1)base case:若当前节点为空,说明不存在。返回not present
或当前节点值等于待删除节点值,则进行删除操作(下方细讲)
2)general case:若当前节点值大于待删除节点值,则转化为对当 前节点的左子树进行删除操作,若 shorter==true,则寻找对应的 操作,并对平衡因子进行修改;若当前节点值小于待删除节点
值,则转化为对当前节点的右子树进行删除操作,若 shorter==true,同上述操作。
删除操作:
若待删除节点的左子树为空,则 sub_root=sub_root->right
若待删除节点的右子树为空,则 sub_root=sub_root->left
若待删除节点的左右子树均不为空,则寻找待删除节点的前驱, 并记录前驱的值,转化为对左子树删除前驱的操作
实现代码:
template<class Record>
Error_code AVL_tree<Record>::remove(Record & old_data)
bool shorter = true;
return avl_remove(root, old_data, shorter);
template<class Record>
Error_code AVL_tree<Record>::avl_remove(Binary_node<Record>*& sub_root, Record & new_data, bool & shorter)
Error_code result;
Record sub_record;
if (sub_root == NULL)
shorter = false;
return not_present;
else if (new_data == sub_root->data)
Binary_node<Record>*to_delete = sub_root;
if (sub_root->right_child == NULL)
sub_root = sub_root->left_child;
shorter = true;
delete to_delete;
return success;
else if (sub_root->left_child == NULL)
sub_root = sub_root->right_child;
shorter = true;
delete to_delete;
return success;
else
to_delete = sub_root->left_child;
Binary_node<Record> *parent = sub_root;
while (!to_delete->right_child)
parent = to_delete;
to_delete = to_delete->left_child;
new_data = to_delete->data; //转化为对前驱的删除
sub_record = new_data;
if (new_data < sub_root->data)
result = avl_remove(sub_root->left_child, new_data, shorter);
if (sub_record.the_key() != 0)sub_root->data = sub_record;
if (shorter == true)
switch (sub_root->get_balance())
case left_higher:
sub_root->set_balance(equal_height);
break;
case equal_height:
sub_root->set_balance(right_higher);
break;
case right_higher:
shorter = right_balance2(sub_root);
break;
if (new_data > sub_root->data)
result = avl_remove(sub_root->right_child, new_data, shorter);
if (shorter == true)
switch (sub_root->get_balance())
case left_higher:
shorter=left_balance2(sub_root);
break;
case equal_height:
break;
sub_root->set_balance(left_higher);
case right_higher:
sub_root->set_balance(equal_height);
break;
return result;
由于删除操作出现的情况多于插入操作(5种),会出现R-,L-两种不同情况,所以左调整(left_balance)和右调整(right_balance)函数需要做修改。
代码如下:
template<class Record>
bool AVL_tree<Record>::right_balance2(Binary_node<Record>*& sub_root)
bool shorter;
Binary_node<Record> *&right_tree = sub_root->right_child;
switch (right_tree->get_balance())
case right_higher: //RR height--
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
rotate_left(sub_root);
shorter = true;
break;
case equal_height: //R- height doesn't change
right_tree->set_balance(left_higher);
rotate_left(sub_root);
shorter = false;
break;
case left_higher: //RL height--
Binary_node<Record> *sub_tree = right_tree->left_child;
switch (sub_tree->get_balance())
case equal_height:
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(equal_height);
right_tree->set_balance(right_higher);
break;
case right_higher:
sub_root->set_balance(left_higher);
right_tree->set_balance(equal_height);
break;
sub_tree->set_balance(equal_height);
rotate_right(right_tree);
rotate_left(sub_root);
shorter = true;
break;
return shorter;
template<class Record>
bool AVL_tree<Record>::left_balance2(Binary_node<Record>*& sub_root)
bool shorter;
Binary_node<Record> *&left_tree = sub_root->left_child;
switch (left_tree->get_balance())
case left_higher: //LL height--
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
rotate_right(sub_root);
shorter = true;
break;
case equal_height: //L- height doesn't change
left_tree->set_balance(right_higher);
rotate_right(sub_root);
shorter = false;
break;
case right_higher: //LR height--
Binary_node<Record> *sub_tree = left_tree->left_child;
switch (sub_tree->get_balance())
case equal_height:
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
break;
case left_higher:
left_tree->set_balance(equal_height);
sub_root->set_balance(right_higher);
break;
case right_higher:
sub_root->set_balance(equal_height);
left_tree->set_balance(left_higher);
break;
sub_tree->set_balance(equal_height);
rotate_left(left_tree);
rotate_right(sub_root);
shorter = true;
break;
return shorter;
5)Splay Tree
①产生意义:
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。spaly tree应运而生。spaly tree是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。 --百度百科
②优缺点:
优点:
1.由于无需存储平衡或者其它的限制信息,它们所需的空间更小。
2.查找和更新算法概念简单,易于实现。
缺点:
1.它们需要更多的局部调整,尤其是在查找期间。(那些有明确限制的数据结构仅需在更新期间进行调整,查找期间则不用)
2.一系列查找操作中的某一个可能会耗时较长,这在实时应用程序中可能是个不足之处。
③操作:
· 左挂(left-link)
算法描述:
目标:将current及其右子树挂到small-key tree上,当前树变小
1) 将last_small的右子树修改为current
2) 将last_small 更新为current
3) 将current更新为current->right
实现代码:
void Splay_tree::link_left(Binary_node<Record>*& current, Binary_node<Record>*& last_small)
last_small->right_child = current;
last_small = current;
current = current->right_child;
· 右挂
算法描述:
目标:将current及其左子树挂到large-key tree上,当前树变小
1) 将first _large的左子树修改为current
2) 将first _large更新为current
3) 将current更新为current->left
实现代码:
void Splay_tree::link_right(Binary_node<Record>*& current, Binary_node<Record>*& first_large)
first_large->left_child = current;
first_large = current;
current = current->left_child;
· 左旋
· 右旋
左旋和右旋操作和avl tree相同,仅贴上代码
实现代码:
void Splay_tree::rotate_left(Binary_node<Record>*& current)
Binary_node<Record> *right_tree = current->right_child;
current->right_child = right_tree->left_child;
right_tree->left_child = current;
current = right_tree;
void Splay_tree::rotate_right(Binary_node<Record>*& current)
Binary_node<Record> *left_tree = current->left_child;
current->left_child = left_tree->right_child;
left_tree->right_child = current;
current = left_tree;
④Splay Tree实现过程
算法描述:
(1) 初始状态:small-key tree 和 large-key tree 为空,central tree为整棵树。
(2) 调整方法: central tree不为空&& central tree的根节点与target不相等时进行调整。每次调整两层。
Target与central tree的根节点比较,判断Target在Central Tree中所位于的路径。
Zig-zag型:执行Link_right Link_left
Zig-Zig型:执行rotate_right Link_right
Zig: 执行Link_right
Zag-Zag:执行rotate_left Link_left
Zag-Zig:执行Link_left Link_right
Zag:执行Link_left
(3) 第二步执行结束时:
判断central tree是否为空:
如果为空,表示target不存在,则将target插入,它的左子树为small-key tree ,右子树为large-key tree。
如果不为空,表示target存在。 central tree的root为最终的根节点,重新调整树的结构即可。
实现代码:
Error_code Splay_tree::Splay(const Record & target)
Binary_node<Record> *dummy = new Binary_node<Record>;
Binary_node<Record> *current = root, *child,
*last_small = dummy, *first_large = dummy;//dummy的左孩子为larger-key tree的根 //dummy的右孩子为smaller-key tree的根
while (current != NULL&¤t->data != target)
if (target < current->data)
child = current->left_child; //zig
if (child == NULL || target == child->data)
link_right(current,first_large);
else if (target < child->data) //zig-zig
rotate_right(current);
link_right(current, first_large);
else //zig-zag
link_right(current, first_large);
link_left(current, last_small);
else if(target > current->data)
child = current->right_child;
if (child == NULL || child->data == target) //zag
link_left(current, last_small);
else if(target>child->data) //zag-zag
rotate_left(current);
link_left(current, last_small);
else //zag-zig
link_left(current, last_small);
link_right(current, first_large);
Error_code result;
if (current == NULL) //not present
current = new Binary_node<Record>(target);
result = entry_inserted;
last_small->right_child = first_large->left_child = NULL;
else //found!
result = entry_found;
last_small->right_child = current->left_child;
first_large->left_child = current->right_child;
root = current;
root->right_child = dummy->left_child;
root->left_child = dummy->right_child;
delete dummy;
return result;
6)Trie(字典树)
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树。
① 定义:一个m阶的Trie包含m个子树(叉)
②作用:通过单词的字母从第一位开始检索,按照拼写顺序,依次寻找,寻找次数由单词长度决定,对于单词查找效率高
③操作:
· 查找
算法描述:
1)对单词的第一位与所对应的字母表的序号对应,并走对应分支
2)对单词的下一位进行同样操作,直至单词的最后一位
3)若location存在且不为空,传出x,否则返回错误信息
代码实现:
Error_code Trie::trie_search(const Key & target, Record & x) const
int position = 0;
char next_char;
Trie_node *location = root;
while (location != NULL &&
(next_char = target.key_letter(position)) != '\\0')
location = location->branch[alphabetic_order(next_char)];
position++;
//调整location至目标点
if (location != NULL && location->data != NULL)
x = *(location->data);//find!
return success;
else//not found
return not_present;
· 插入
算法描述:
1)从root开始,根据单词的第一个字母对应的序号,走对应的分支,若对应节点为空,则new一个节点
2)对单词的下一位进行同样操作,直至单词的最后一位
3)若location存在且不为空返回错误信息,否则插入单词
代码实现:
Error_code Trie::insert(const Record & new_entry)
Error_code result = success;
if (root == NULL) root = new Trie_node;//根节点为空
int position = 0;
char next_char;
Trie_node *location = root;
while (location != NULL &&
(next_char = new_entry.key_letter(position)) != '\\0')
int next_position = alphabetic_order(next_char);
if (location->branch[next_position] == NULL)//没“路”开“路”
location->branch[next_position] = new Trie_node;
location = location->branch[next_position];
position++;
//定位到目标位置
if (location->data != NULL) result = duplicate_error;
else location->data = new Record(new_entry);
return result;
7)B Tree
①定义:
一个m阶的B-Tree
· 所有的叶子节点都在同一层
· 所有除了根节点以外的内部节点至多有m个非空的孩子,并且至少有m/2上取整个非空孩子
· 所有内部节点的关键码个数总比其非空孩子数少一
· 根节点至多有m个孩子,至少有两个孩子,或该树中只有根节点一个
②操作
· 查找:
辅助函数:
Search Node:查找当前及节点中是否存在,目标关键码,若存在返回position及success,否则返回目标关键码可能存在的分支的position
实现代码:
template<class Entry, int order>
Error_code B_tree<Entry, order>::search_node(B_node<Entry, order>* current, const Entry & target, int & position)
/*查找当前节点是否存在target,若存在返回position,不存在,返回target应该存储的branch的位置*/
position = 0;
while (current->count > position&¤t->data[position] < target)
position++;
if (position < current->count&¤t->data[position] == target)
return success;
else return not_present;
查找算法描述:递归实现
1)base case:对当前节点进行search node操作成功,将数据拷贝给target,结束递归
2)gengral case:对当前节点进行search node操作失败,转换为对相应branch的search操作
实现代码:
template<class Entry, int order>
Error_code B_tree<Entry, order>::search_tree(Entry & target)
return recursive_search_tree(root, target);
template<class Entry, int order>
Error_code B_tree<Entry, order>::recursive_search_tree(B_node<Entry, order>* current, Entry & target)
Error_code result = not_present;
int position = 0;
if (current != NULL)
result = search_node(current, target, position);
if (result == not_present)
result = recursive_search_tree(current->branch[position], target);
else
target = current->data[position];
return result;
· 插入:
辅助函数:
Push in:对给定节点的给定位置进行插入操作
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::push_in(B_node<Entry, order>* current, const Entry & entry, B_node<Entry, order>* right_branch, int position)
/*在给定position处插入data*/
for (int i = current->count; i > position; i--)
current->data[i] = current->data[i - 1];
current->branch[i + 1] = current->branch[i];
current->data[position] = entry;
current->branch[position + 1] = right_branch;
current->count++;
Split node:对给定节点,给定待插入关键码,给定待插入指针,给定位置进行插入,返回分裂后产生的新节点的指针,以及分裂产生的中间关键码。
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::split_node(B_node<Entry, order>* current, const Entry & extra_entry, B_node<Entry, order>* extra_branch, int position, B_node<Entry, order>*& right_half, Entry & median)
right_half = new B_node<Entry, order>;
int mid = order / 2;
if (position <= mid) //待插入节点位于一半的左边
for (int i = mid; i < order - 1; i++)
right_half->data[i-mid] = current->data[i];
right_half->branch[i - mid + 1] = current->branch[i + 1];
current->count = mid;
right_half->count = order - mid - 1;
push_in(current, extra_entry, extra_branch, position);
//在current的position处正常插入data
else //待插入节点位于一半的右边
mid++;
for (int i = mid; i < order - 1; i++)
right_half->data[i - mid] = current->data[i];
right_half->branch[i - mid + 1] = current->branch[i + 1];
current->count = mid;
right_half->count = order - mid - 1;
push_in(right_half, extra_entry, extra_branch, position-mid);
//在right-half的position-mid处正常插入data
median = current->data[current->count - 1];//remove median
right_half->branch[0] = current->branch[current->count];//move median‘s branch to right-half
current->count--;
Push down:对给定节点,给定关键码进行插入操作,若插入过程中产生饱和情况,则进行分裂并返回中间关键码,以及分裂产生的新节点的指针。
算法描述:递归实现
1)base case:当传入的current指针为空时,对空指针插入,默认进行分裂,产生的中间值为插入的关键码,产生的新节点的指针默认为空,并结束递归
2)gengral case:当前节点不为空,则对当前节点进行search node操作,若查找成功,返回重复错误信息,否则转换为对相应的branch进行push down操作,若产生溢出结果,则分析当前节点是否能够容纳下分裂产生的新节点,若能满足,则进行push in操作,若不满足,则进行分裂操作
实现代码:
template<class Entry, int order>
Error_code B_tree<Entry, order>::push_down(B_node<Entry, order>* current, const Entry & new_entry, Entry & median, B_node<Entry, order>*& right_branch)
Error_code result;
int position;
if (current == NULL)
median = new_entry;
right_branch = NULL;
result = overflow;
else
if (search_node(current, new_entry, position) == success)
return duplicate_error;
Entry extra_entry;
B_node<Entry, order> *extra_branch;
result = push_down(current->branch[position], new_entry, extra_entry, extra_branch);//转换为对branch的插入
if (result == overflow)
if (current->count < order - 1) //当前节点未达到饱和
result = success;
push_in(current, extra_entry, extra_branch, position);
else split_node(current, extra_entry, extra_branch, position, right_branch, median);//饱和分裂
return result;
插入算法描述:递归实现
1)对root节点进行push down操作
2)若push down返回溢出,则产生一个新的树节点,树的高度将增加
同时
产生的新的根为median
左孩子为原来的root,右孩子为push down返回的分裂产生的新节点
更新root
实现代码:
template<class Entry, int order>
Error_code B_tree<Entry, order>::insert(const Entry & target)
Entry median;
B_node<Entry, order> *right_branch, *new_root;
Error_code result = push_down(root, target, median, right_branch);
if (result == overflow)
new_root = new B_node<Entry, order>;
new_root->count = 1;
new_root->data[0] = median;
new_root->branch[0] = root;
new_root->branch[1] = right_branch;
root = new_root;
result = success;
return result;
· 删除:
辅助函数:
Remove data:对给定节点的给定位置的关键码进行删除
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::remove_data(B_node<Entry, order>* current, int position)
for (int i = position; i < current->count - 1; i++)
current->data[i] =current->data[i + 1];
current->count--;
copy_in_predecessor:对给定节点的给定位置,做一个寻找前驱,并将当前位置的关键码的值修改为前驱的值
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::copy_in_predecessor(B_node<Entry, order>* current, int position)
/*找到前驱,并将当前节点的data修改为前驱的data值*/
B_node<Entry, order> *tmp = current->branch[position];
while (tmp->branch[tmp->count] != NULL)
tmp = tmp->branch[tmp->count];
current->data[position] = tmp->data[tmp->count - 1];
Move left:已知当前节点的branch[position-1]位置关键码数量由于删除不满足b-tree定义,同时branch[position]的数量允许借出一个关键码时,对current,branch[position-1],branch[position]三个节点进行move left操作
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::move_left(B_node<Entry, order>* current, int position)
/*左孩子结点数量不足,将当前节点的但前位置的关键码添加给给左孩子的最后一个位置,
相邻的右孩子的第一个节点替换当前节点的当前位置,并对右孩子做左移操作(包括branch),同时,右孩子的第一个branch调整给左孩子的最后位置*/
B_node<Entry, order> *left_branch = current->branch[position - 1];
B_node<Entry, order> *right_branch = current->branch[position];
left_branch->data[left_branch->count] = current->data[position - 1];
//data 根->左
left_branch->branch[++left_branch->count] = right_branch->branch[0];
//branch 右[0]->左[count]
current->data[position - 1] = right_branch->data[0];//data右->根
right_branch->count--; //右孩子关键码数量--
for (int i = 0; i < right_branch->count; i++) //右孩子进行右移操作
right_branch->data[i] = right_branch->data[i + 1];
right_branch->branch[i] = right_branch->branch[i + 1];
right_branch->branch[right_branch->count] = right_branch->branch[right_branch->count + 1];
Move right:已知当前节点的branch[position+1]关键码数量由于删除不满足b-tree定义,同时branch[position]的数量允许借出一个关键码时,对current,branch[position], branch[position+1]三个节点进行moveright操作
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::move_right(B_node<Entry, order>* current, int position)
/*右孩子结点数量不足,对右孩子做右移操作(包括branch)腾出空间接收新关键码,
然后将当前节点的当前位置的关键码添加给给右孩子的第一个位置,同时,左孩子的
最后一个branch调整给右孩子的第一个位置,相邻的左孩子的最后一个节点替换当前
节点的当前位置
*/
B_node<Entry, order> *left_branch = current->branch[position];
B_node<Entry, order> *right_branch = current->branch[position+1];
right_branch->branch[right_branch->count + 1] = right_branch->branch[right_branch->count];
for (int i = right_branch->count; i > 0; i--)
right_branch->data[i] = right_branch->data[i - 1];
right_branch->branch[i] = right_branch->branch[i - 1];
right_branch->count++;
right_branch->data[0] = current->data[position];
right_branch->branch[0] = left_branch->branch[left_branch->count--];
current->data[position] = left_branch->data[left_branch->count];
Combine:已知相邻的节点不存在足够的关键码可以借出时,将两个节点(branch[position],branch[position-1])进行合并操作
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::combine(B_node<Entry, order>* current, int position)
/*合并操作:将current[position-1]放置到左孩子的最后一个位置,将右孩子依次接到
左孩子的后面(包括branch),最后调整current(从position-1依次将data和branch左移)
*/
B_node<Entry, order> *left_branch = current->branch[position - 1];
B_node<Entry, order> *right_branch = current->branch[position];
left_branch->data[left_branch->count] = current->data[position - 1];//current[position-1]复制到左孩子
left_branch->branch[++left_branch->count] = right_branch->branch[0];
for (int i = 0; i < right_branch->count; i++) //复制right-branch
left_branch->data[left_branch->count] = right_branch->data[i];
left_branch->branch[++left_branch->count] = right_branch->branch[i + 1];
current->count--;
for (int i = position - 1; i < current->count; i++) //调整current
current->data[i] = current->data[i + 1];
current->branch[i + 1] = current->branch[i + 2];
delete right_branch;
Restore:利用move left,move right,combine,操作,综合完成由于删除带来的数量不足的问题
实现代码:
template<class Entry, int order>
void B_tree<Entry, order>::restore(B_node<Entry, order>* current, int position)
/*解决删除后data数量不满足B-Tree定义的情况*/
if (position == current->count) //最右侧情况
if (current->branch[position - 1]->count > (order - 1) / 2)
move_right(current, position - 1);
else
combine(current, position);
else if (position == 0) //最左侧情况
if (current->branch[1]->count > (order - 1) / 2)
move_left(current, 1);
else
combine(current, 1);
else //一般情况
if (current->branch[position - 1]->count > (order - 1) / 2)
move_right(current, position - 1);
else if (current->branch[position + 1]->count > (order - 1) / 2)
move_left(current, position + 1);
else
combine(current, position);
删除算法描述:递归实现
算法描述:
1)base case:若当前传入current指针为空,则返回not present;或当查找到待删除节点为叶子节点时直接删除,并返回success
2)general case:当search node操作成功,且非叶子节
以上是关于[数据结构]tree-form data structure summary的主要内容,如果未能解决你的问题,请参考以下文章