数据的核密度估计及其可视化:Python实现
Posted zhuo木鸟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据的核密度估计及其可视化:Python实现相关的知识,希望对你有一定的参考价值。
文章目录
本文的参考文献主要如下:
- Silverman B.W. Density Estimation. Chapman and Hall, London, 1986
- 标准 ISO 13528
实例数据介绍
本博客采用的示例数据为本博客的参考文献一中的表 2.1 和 2.2,如下所示:
精神疾病治疗时长数据表

间歇泉爆发持续时间数据表

文件放置介绍
我们将上述的数据表放置在代码文件夹,所在路径的另一个命名为 “数据” 的文件夹中:
代码:
-------> xxx.py (代码)
数据:
-------> 间歇泉爆发持续时间表
-------> 自杀倾向治疗时间
频率分布直方图法
原理探讨与分析
设数据集为 X = ( X 1 , X 2 , ⋯ , X n ) X=(X_1, X_2, \\cdots, X_n) X=(X1,X2,⋯,Xn):
频率分布直方图需要我们提供画图原点
x
0
x_0
x0 以及一个带宽
h
h
h,将落在
[
x
0
+
(
m
−
1
)
⋅
h
,
x
0
+
m
⋅
h
]
[x_0 + (m-1)\\cdot h, x_0 + m \\cdot h]
[x0+(m−1)⋅h,x0+m⋅h] 上的点的数量进行计数,后除以带宽长度即可:
f
^
(
x
)
=
1
n
h
(
落在与
x
同一带宽上的
X
i
的数量
)
\\hatf(x) = \\frac1nh (\\text落在与 x \\text同一带宽上的 X_i \\text的数量)
f^(x)=nh1(落在与x同一带宽上的Xi的数量)
一般的在对数据进行分析时,常用频率分布直方图,对数据进行初步的可视化,我们将精神疾病治疗时长数据表,与间歇泉爆发持续时间数据表进行频率分布直方图画图,如下所示:

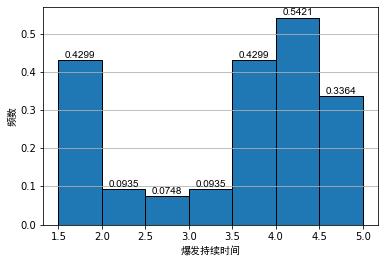
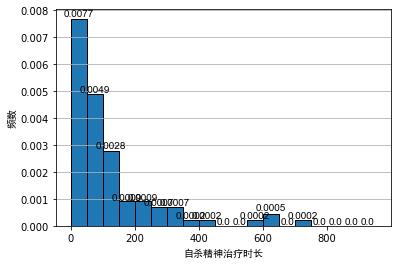
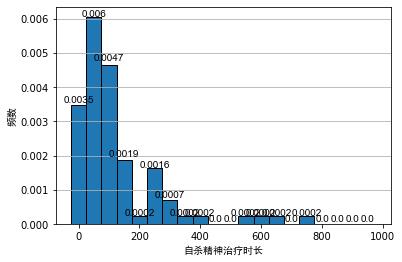
从上图可以看出,即便带宽相同,直方图的原点不同会导致直方图具有不同的视觉效果。对于间接泉的爆发持续时间直方图来说,虽然第1个图和第2个图都表现出明显的双峰分布,但是对于图2来说双峰的间隔点难以看出。
对于精神疾病治疗时长的直方图来说,第2个图在区 [ 150 , 250 ] [150, 250] [150,250] 时,可以看出一个次峰。对于非统计学者来说,很可能会造成数据呈现双峰分布的误解。毕竟从图1来看这很可能是由随机性导致的。
Python 代码实现
# -*- coding: utf-8 -*-
"""
Created on Sun Sep 19 10:11:15 2021
@author: zhuozb
本代码主要展示了 13528 参考文献 30 里的第二节中,有关 histogram 的用例讨论。
本代码主要讨论了间歇泉爆发性持续时间,以及自杀精神治疗时间的频数分布画图。
"""
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def extract_data(path):
# 将Excel数据表读入Python中
table = pd.read_excel(path, header=None)
# 将数据表转换为 2D 数列
data = table.values
# 剔除非数字数据并将一维数列转换为二维数列
data = data[~np.isnan(data)]
return data
def plot_histogram(data, bins='auto', title=''):
#
fig, ax = plt.subplots()
# 直接使用 plt.hist 画图
freq, bins, patches = plt.hist(data,
bins=bins,
density=True,
edgecolor='black')
# 频数分布直方图的标签位置
bin_centers = np.diff(bins)*0.5 + bins[:-1]
for fr, x, patch in zip(freq, bin_centers, patches):
height = round(fr, 4)
plt.annotate("".format(height),
xy = (x, height), # top left corner of the histogram bar
xytext = (0,0.2), # offsetting label position above its bar
textcoords = "offset points", # Offset (in points) from the *xy* value
ha = 'center', va = 'bottom',
fontfamily='arial') # 还用a字体展示标签
# 自动的调整X轴和Y轴的显示范围,虽然没有什么用
ax.set_xlim(auto=True)
ax.set_ylim(auto=True)
# 设置X轴和Y轴的标签
if title != '':
# 如果没有给出标题,则不显示X轴的标签
plt.xlabel(title, fontfamily='simhei')
plt.ylabel('频数', fontfamily='simhei')
plt.grid(axis='y')
if __name__ == '__main__':
eruption_lenght_path = r'../数据/间歇泉爆发持续时间表.xlsx'
treatment_spell_path = r'../数据/自杀倾向治疗时间.xlsx'
# 读取数据集
# 读取数据表格 2.1
treatment_spell_data = extract_data(treatment_spell_path)
# 画出表格2.2
eruption_lenght_data = extract_data(eruption_lenght_path)
# 画出图2.1
plot_histogram(eruption_lenght_data, bins=np.arange(1.25, 5.5, 0.5), title='爆发持续时间')
plot_histogram(eruption_lenght_data, bins=np.arange(1.5, 5.5, 0.5), title='爆发持续时间')
# 画出图2.2
plot_histogram(treatment_spell_data, bins=np.arange(0, 1000, 50), title='自杀精神治疗时长')
plot_histogram(treatment_spell_data, bins=np.arange(-25, 1000, 50), title='自杀精神治疗时长')
简单核密度估计法
原理探讨与分析
简单核密度的估计法的原理是将频率分布直方图的带宽设置为接近于0,对于一个概率密度函数来说都有:
f
(
x
)
=
lim
h
→
0
1
2
h
P
(
x
−
h
<
X
<
x
+
h
)
f(x) = \\lim_h\\to0 \\frac12h P(x-h < X < x+h)
f(x)=h→0lim2h1P(x−h<X<x+h)
于是我们可以用带宽为无限小的频数分布图来估计概率密度:
f
^
(
x
)
=
1
2
n
h
(
落在带宽
(
x
−
h
,
x
+
h
)
上的
X
i
的数量
)
\\hatf(x) = \\frac12nh (\\text落在带宽 (x-h, x+h) \\text上的 X_i \\text的数量)
f^(x)=2nh1(落在带宽(x−h,x+h)上的Xi的数量)
为了方便表述我们定义一个核密度函数如下所示:
w
(
x
)
=
1
2
if
∣
x
∣
<
1
0
otherwise.
w(x)= \\begincases\\frac12 & \\text if |x|<1 \\\\ 0 & \\text otherwise. \\endcases
w(x)=210 if ∣x∣<1 otherwise.
于是,
f
^
(
x
)
\\hatf(x)
f^(x) 可以表示为:
f
^
(
x
)
=
1
h
n
∑
i
=
1
n
w
(
x
−
X
i
h
)
\\hatf(x) = \\frac1hn \\sum_i=1^n w ( \\fracx-X_ih )
f^(x)=hn1i=1∑nw(hx−Xi)
在实际应用中带宽当然可以不需要取到无限接近于0,以间歇泉爆发持续时间为例,我们可以将带宽设置为0.25画出的简单核密度图如下所示:

由于我们的经验密度函数 f ^ ( x ) \\hatf(x) f^(x)不是一个连续函数,在中断点处是不可导的。从上图也可以直观的看出,这种图像对于未经学习的学者来说,图像中的阶跃部分可能具有一定的迷惑性。
Python代码实现
# -*- coding: utf-8 -*-
"""
Created on Sun Sep 19 11:37:22 2021
@author: zhuozb
这是ISO13528中的参考文献,30里面的2.3小节的案例画图
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from histogram_example_showing import extract_data
def digits_after_decimal(num):
'''
返回变量 num 的小数点位数
'''
num = str(num)
# 小数点所在位置
digit_loc = num.find('.')
# 小数点后的位数
digits_decimal = len(num) - digit_loc - 1
return digits_decimal
def plot_naive_estimator(data, bandwidth=0.25, title=''):
'''
data :待统计的数据
bandwidth:画图带宽
title:画出图像的标题,如果不给则默认不写出标题
'''
fig, ax = plt.subplots()
# n 为样本容量
n = len(data)
# 返回数列中最小的数,并根据这个数来产生(极限)间隔范围
min_num = min(data)
# 找出最小数的小数点后的位数
digits_decimal = digits_after_decimal(min_num)
# 画图点间隔
data_interval = 0.1**(digits_decimal)
# 求出数列中的最大数,以此来产生画图范围
max_num = max(data)
# 产生X轴的画图点
xtick_array = np.arange(0.9*min_num if (min_num>0) else 1.1*min_num,
1.1*max_num, data_interval)
# 产生Y轴的画图点
ytick_array = []
def calculate_y(x, x_data, bandwidth):
# 根据公式2.1求解,X对应的Y
y_sum = 0
for x_i in data:
# 根据 (x-X)/h 从数据数列中产生一个权重数列
weight_array = np.abs((x - x_i)/bandwidth)
# 根据公式2.1, 将权重数列按条件求和
sum_weight = len(weight_array[(weight_array < 1)])/2
y_sum = y_sum + sum_weight
#
y = y_sum/(n*bandwidth)
return y
ytick_array = [calculate_y(x, data, bandwidth) for x in xtick_array]
# 设置X轴和Y轴的标签
if title != '':
# 如果没有给出标题,则不显示X轴的标签
plt.xlabel(title, fontfamily='simhei')
plt.ylabel('概率密度估计', fontfamily='simhei')
plt.plot(xtick_array, ytick_array, linewidth=1)
# 设置网格线
plt.grid(axis='both')
if __name__ == '__main__':
eruption_lenght_path = r'../数据/间歇泉爆发持续时间表.xlsx'
treatment_spell_path = r'../数据/自杀倾向治疗时间.xlsx'
# 读取数据集
# 读取数据表格 2.1
treatment_spell_data = extract_data(treatment_spell_path)
# 画出表格2.2
eruption_lenght_data = extract_data(eruption_lenght_path)
plot_naive_estimator(eruption_lenght_data, title=f'爆发持续时间,h = 0.25')
核密度估
以上是关于数据的核密度估计及其可视化:Python实现的主要内容,如果未能解决你的问题,请参考以下文章